素数判定方法,方法持续更新...

　　素数定义：质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数。

　　方法一（暴力法）：素数问题变化莫测，但万变不离其宗。素数问题最核心的就是如何判断一个数是否是素数。对于判断一个数m是否是素数，最原始的方法就是按照素数的定义，试除2开始到m-1的整数，如果无一例外地都不能整除，则该数一定是素数。实现程序如下：

//============================
//判断是否是素数1
//============================
#include <iostream>
using namespace std;

int main() {
    cout << "please inpout a number.";
    int m;
    cin >> m;
    for (int i = 2; i < m; ++i)
        if (m%i == 0) {
            cout << m << " isn't a prime\n";
            return 1;
        }
    cout << m << " is a prime\n";
    return 0;
}

　　方法二（暴力法改进）：我们知道如果一个数有因子的话，那么在它的平方根数以内就应该有，否则就没有因子。例如66的平方根在8与9之间，因为66不是素数，，则它一定有比8还小的因子，我们知道66的因子是2、3、6等。

　　现在我们就可以将m试除2到√m的整数，如果无一例外地都不能整除，则该数一定是素数。实现程序如下：

//============================
//判断是否是素数法2
//============================
#include <iostream>
using namespace std;
int main() {
    cout << "please inpout a number.";
    int m;
    cin >> m;
    double sqrtm = sqrt(m*1.0);
    for (int i = 2; i <= sqrtm; ++i)
        if (m%i == 0) {
            cout << m << " isn't a prime\n";
            return 1;
        }
    cout << m << " is a prime\n";
    return 0;
}

　　方法三（暴力法进一步改进）：现在举个例子，判断102是否是素数，本来要从2试除到10。但事实上，中间的4、6、8、10也都无须试，只需要试除2、3、5、7。直接来说，就是只需要试除2到√m之间的所有素数即可。而所有素数（除了2和3）都满足6*i-1或6*i+1（i=1、2、3...）。那么代码又可以改进，如下：

//============================
//判断是否是素数法3
//============================
#include <iostream>
using namespace std;
int main() {
    cout << "please inpout a number.";
    int m;
    cin >> m;
    //两个较小数另外处理
    if (m == 2 || m == 3)
        return 1;
    double sqrtm = sqrt(m*1.0);
    for (int i = 5; i <= sqrtm; i += 6)
        if (m %i == 0 || m % (i + 2) == 0)
            cout << m << " isn't a prime\n";
    cout << m << " is a prime\n";
    return 0;
}

　　下面这种方法也是本人借鉴别人的，如有侵权请联系我删除。

　　方法四（筛选法）：素数有2、3、5、7、11、13、17、19、23、29...，观察可知：素数一定在6的倍数的左右，但6的倍数的左右不一定是素数，如23是素数，但25不是素数。则我们可以先通过这个条件将可能是素数的数筛选出来，然后采用方法三，代码如下：

//============================
//判断是否是素数法4
//============================
#include <iostream>
using namespace std;
int main() {
    cout << "please inpout a number.";
    int m;
    cin >> m;
    //两个较小数另外处理
    if (m == 2 || m == 3)
        return 1;
    //不在6的倍数两侧的一定不是质数
    if (m % 6 != 1 && m % 6 != 5) {
        cout << m << " isn't a prime\n";
        return 0;
    }

    double sqrtm = sqrt(m*1.0);
    //在6的倍数两侧的也可能不是质数
    for (int i = 5; i <= sqrtm; i += 6)
        if (m %i == 0 || m % (i + 2) == 0)
            cout << m << " isn't a prime\n";
    //排除所有，剩余的是质数
    cout << m << " is a prime\n";
    return 0;
}

现在对这四种方法的效率进行测试，测试代码如下：

#include <iostream>
#include <ctime>
using namespace std;

int isPrime_1(int num);
int isPrime_2(int num);
int isPrime_3(int num);
int isPrime_4(int num);
int main() {
    int num = 30000;
    int tstart, tstop; //分别记录起始和结束时间

                       //测试第一个判断质数函数
    tstart = clock();
    for (int i = 1; i <= num; i++)
        isPrime_1(i);
    tstop = clock();
    cout << "isPrime_1方法的时间(ms):" << tstop - tstart << endl;

    //测试第二个判断质数函数
    tstart = clock();
    for (int i = 1; i <= num; i++)
        isPrime_2(i);
    tstop = clock();
    cout << "isPrime_2方法的时间(ms):" << tstop - tstart << endl;

    //测试第三个判断质数函数
    tstart = clock();
    for (int i = 1; i <= num; i++)
        isPrime_3(i);
    tstop = clock();
    cout << "isPrime_3方法的时间(ms):" << tstop - tstart << endl;

    //测试第四个判断质数函数
    tstart = clock();
    for (int i = 1; i <= num; i++)
        isPrime_4(i);
    tstop = clock();
    cout << "isPrime_4方法的时间(ms):" << tstop - tstart << endl;
    cout << endl;
    return 0;
}

int isPrime_1(int num) {
    for (int i = 2; i <= num - 1; i++)
        if (num %i == 0)
            return 0;
    return 1;
}

int isPrime_2(int num) {
    double sqrtnum = sqrt(num*1.0);
    for (int i = 2; i <= sqrtnum; i++)
        if (num %i == 0)
            return 0;
    return 1;
}

int isPrime_3(int num) {
    //两个较小数另外处理
    if (num == 2 || num == 3)
        return 1;
    double sqrtnum = sqrt(num*1.0);
    for (int i = 5; i <= sqrtnum; i += 6)
        if (num %i == 0 || num % (i + 2) == 0)
            return 0;
    return 1;
}

int isPrime_4(int num) {
    //两个较小数另外处理
    if (num == 2 || num == 3)
        return 1;
    //不在6的倍数两侧的一定不是质数
    if (num % 6 != 1 && num % 6 != 5)
        return 0;
    double sqrtnum = sqrt(num*1.0);
    //在6的倍数两侧的也可能不是质数
    for (int i = 5; i <= sqrtnum; i += 6)
        if (num %i == 0 || num % (i + 2) == 0)
            return 0;
    //排除所有，剩余的是质数
    return 1;
}

判断1-30000之间素数的耗时：

现在测试判断1-300000之间素数的耗时：

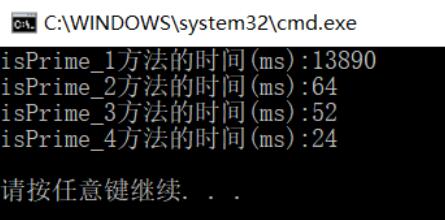
方法二和方法三的效率之间相差其实不大，什么原因大家可以思考思考。

　　方法五（厄拉多塞筛法）：如果我们在进行顺序遍历时，每取得一个数（排除0、1），如果将它所有的倍数（排除0、1、本身）都清除，那么，剩下的数是不是必为素数？

　　没错，这个有趣且实用的方法便是著名的厄拉多塞筛法！

　　对此，我们可以声明一个长度为最大限制数的布尔数组。用布尔值来区别筛选出的数和质数。运用厄拉多塞筛法得代码如下：

int countPrimes(int n) {
    int count = 0;
    //初始默认所有数为质数
    vector<bool> signs(n, true);
    for (int i = 2; i < n; i++) {
        if (signs[i]) {
            count++;
            for (int j = i + i; j < n; j += i) {
                //排除不是质数的数
                signs[j] = false;
            }
        }
    }
    return count;
}

链接：https://leetcode-cn.com/problems/count-primes/solution/ji-shu-zhi-shu-bao-li-fa-ji-you-hua-shai-fa-ji-you/
来源：力扣（LeetCode）

　　方法六：本人又学到一种以时间换空间的素数判断方法，现在先将点预备知识，C++的 bitset 在 bitset 头文件中，位集bitset是一种关联容器，因为位集编程简单，效率也不错。bitset中只有0、1，且每个元素占一位。用法：

　　构造函数

　　bitset常用构造函数有四种，如下：

bitset<4> bitset1;　　//无参构造，长度为４，默认每一位为０

bitset<8> bitset2(12);　　//长度为８，二进制保存，前面用０补充

string s = "100101";
bitset<10> bitset3(s);　　//长度为10，前面用０补充
    
char s2[] = "10101";
bitset<13> bitset4(s2);　　//长度为13，前面用０补充

cout << bitset1 << endl;　　//0000
cout << bitset2 << endl;　　//00001100
cout << bitset3 << endl;　　//0000100101
cout << bitset4 << endl;　　//0000000010101

　　可用函数

bitset<8> foo ("10011011");

cout << foo.count() << endl;　　//5　　（count函数用来求bitset中1的位数，foo中共有５个１
cout << foo.size() << endl;　　 //8　　（size函数用来求bitset的大小，一共有８位
cout << foo.test(0) << endl;　　//true　　（test函数用来查下标处的元素是０还是１，并返回false或true，此处foo[0]为１，返回true
cout << foo.test(2) << endl;　　//false　　（同理，foo[2]为０，返回false

cout << foo.any() << endl;　　//true　　（any函数检查bitset中是否有１
cout << foo.none() << endl;　　//false　　（none函数检查bitset中是否没有１
cout << foo.all() << endl;　　//false　　（all函数检查bitset中是全部为１

　　现在言归正传来讲如何判断素数，加入要我们判断2到1亿之间有多少素数，首先我们可以调用上面的方法1亿次，到当你这样干的时候，估计你电脑要运行几十分钟才能有结果。现在我们就采用空间换时间的方法。设置一个空间为1亿的bitset来标记哪些是素数，因为我们知道如果一个数不是素数，那么它的倍数也肯定不是素数。借助这个思想，我们有如下程序：

//=====================================
//利用bitset判断2到1亿之间的素数个数
//=====================================
#include<iostream>
#include<bitset>
using namespace std;

int main() {
    bitset<100000000> *p=new bitset<100000000>;
    p->set();    //每个元素置1
    for (int i = 2; i <= 10000; ++i)
        if (p->test(i))    //第i位为0返回false,为1返回true;
            for (int j = i*i; j < p->size(); j += i)
                p->reset(j);    //每个元素置0
    int num = 0;
    for (int i = 2; i < 100000000; ++i)
        if (p->test(i))
            num++;
    cout << num << endl;
    delete[] p;
    return 0;
}