「TAOI-2」Ciallo～(∠・ω< )⌒★ 题解

手玩了一个小时终于做出来了，这不得写一篇题解记录一下？？

下面设 \(s\) 的长度为 \(n\)，\(t\) 的长度为 \(m\)。

考虑分类讨论：

如果 \(s\) 中有一个子串 \(s'\) 与 \(t\) 完全相同（可以用哈希进行比较），设 \(s'\) 是 \(s\) 的第 \(l\) 到第 \(r\) 个字符组成的字符串，则我们可以删除 \([1,l-1]\) 或者 \([r+1,n]\) 的某一个子区间，计算出它们的总个数就是 \(\dfrac{l\times (l-1)}{2}\) 和 \(\dfrac{(n-r)\times (n-r+1)}{2}\)，两者之和就是这一种情况的方案数。

我们也可以选定一个子串 \(s'\)，满足 \(s'\) 的某一段前缀 \(pre\) 和某一段后缀 \(suc\) 不相交且两者连接到一起就是 \(t\)。这样的话我们删掉 \(pre\) 和 \(suc\) 中间的字符就符合条件了。

例如 ciaohallo 要变成 ciallo 就可以选取前缀 cia 和后缀 llo，它们拼在一起就是我们要得到的字符串。值得注意的是，为了避免掉与上一种情况出现重复计算，我们需要满足 \(pre\) 和 \(suc\) 中间必须留有至少一个字符。在上面的例子中，\(pre\) 和 \(suc\) 之间就留有 oha 这一段字符。

但是怎么计算满足上述条件的 \(s'\) 的个数呢？我们可以设 \(p_i\) 表示 \(s\) 的第 \(i\) 个到第 \(n\) 个字符与 \(t\) 的最大公共前缀的长度，\(q_i\) 表示 \(s\) 的第 \(1\) 个到第 \(i\) 个字符与 \(t\) 的最大公共后缀的长度。对于 \(\forall i\in [1,n],j\in[i+m,n]\)，如果有 \(p_i+q_j≥m\)，则区间 \([i,j]\) 组成的子串 \(s'\) 就是满足条件的。当然 \(s'\) 变成 \(t\) 的删除方法也会有不同的代价。但是我们其实可以推出这个代价就是 \(p_i+q_j-m+1\)。

为什么是对的？我们来看一下这张图：

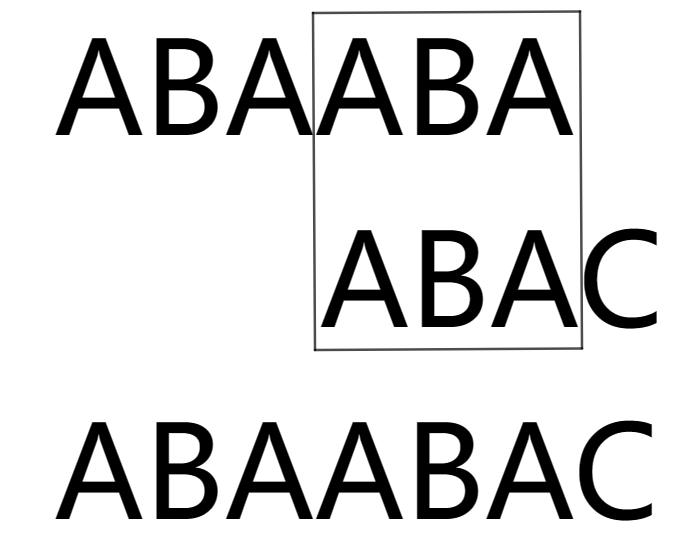
图中第一行是 \([i,i+p_i-1]\) 的字符串 \(A\)，第二行是 \([j-q_j+1,j]\) 的字符串 \(B\)，我们有 \(p_i=6,q_j=4,m=7\)，则 \(p_i+q_j≥m\)，这个时候我们将它们进行对齐就得到了这张图。由于 \(p_i+q_j≥m\)，所以 \(A\) 和 \(B\) 一定有重合部分。由图可知重合部分的长度为 \(p_i+q_j-m=3\)。

我们可以考虑 \(pre\) 的选择方法，进行得到唯一确定的 \(suc\) 的选择方法。我们的 \(pre\) 可以选择 ABA，ABAA，ABAAB，ABAABA，即重合部分的长度加一 \(p_i+q_j-m+1\)。不难发现 \(pre\) 最长的时候就是取 \(A\)，最短的时候就是取 \(A\) 中不与 \(B\) 重合的部分。这个结合图片应该是非常好理解的，大家可以自己思考一下。

综上所述，对于每一个 \(i\)，我们找到所有的 \(j\in[i+m,n]\) 满足 \(p_i+q_j≥m\)，给答案增加 \(p_i+q_j-m+1\)。当然我们还需要事先让 \(p_i,q_j\) 与 \(m-1\) 取一个最小值，因为当 \(p_i\) 或者 \(q_j\) 等于 \(m\) 时，就会和第一种情况算重。

可是暴力找是 \(O(n^2)\) 的，我们需要优化。条件 \(p_i+q_j≥m\iff q_j≥m-p_i\)，所以每一个 \(q_j\) 都是在 \([m-p_i,m-1]\) 内的，这样我们就不难想到权值线段树，储存区间范围内的 \(sum=\sum q_j\) 以及 \(q_j\) 的个数 \(num\)。则对于每一个 \(i\)，它所带来的代价就是 \(sum+num\times (p_i-m+1)\)。

然后就可以愉快地打出代码了：

#include<bits/stdc++.h>
#define Q(id,x,y,flag) query(1,1,id,x,y,flag)
using namespace std;
const int MAXN=4e5+5;
const unsigned long long base=179;
int n,m;
char a[MAXN],b[MAXN];
unsigned long long mul[MAXN],Hash1[MAXN],Hash2[MAXN];
int p[MAXN],q[MAXN];
struct node
{
	long long sum;
	int num;//sum表示和，num表示个数
}T[MAXN<<2];
void pushup(int x){ T[x].num=T[x<<1].num+T[x<<1|1].num,T[x].sum=T[x<<1].sum+T[x<<1|1].sum; }
void change_tree(int x,int l,int r,int k)
{
	if(l>r) return;
	if(l==r)
	{
		T[x].sum+=l,T[x].num++;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid)  change_tree(x<<1,l,mid,k);
	else    change_tree(x<<1|1,mid+1,r,k);
	pushup(x);
}
long long query(int x,int l,int r,int L,int R,int flag)
{
	if(L>R) return 0;
	if(L<=l&&r<=R)
	{
		if(!flag)   return T[x].sum;
		return T[x].num;
	}
	int mid=(l+r)/2;
	long long res=0;
	if(L<=mid)  res+=query(x<<1,l,mid,L,R,flag);
	if(R>mid)   res+=query(x<<1|1,mid+1,r,L,R,flag);
	return res;
}
long long solve(int x){ return 1ll*x*(x+1)/2; }
int main()
{
	cin>>(a+1)>>(b+1);
	n=strlen(a+1),m=strlen(b+1);
	mul[0]=1;
	for(int i=1;i<=n;i++)   Hash1[i]=Hash1[i-1]*base+a[i],mul[i]=mul[i-1]*base;//哈希预处理
	for(int i=1;i<=m;i++)   Hash2[i]=Hash2[i-1]*base+b[i];
	for(int i=1;i<=n;i++)
	{
		if(a[i]!=b[1])  continue;
		int l=1,r=min(n-i+1,m);
		while(l<=r)//二分找最长公共前缀
		{
			int mid=(l+r)/2;
			if(Hash1[i+mid-1]-Hash1[i-1]*mul[mid]==Hash2[mid])  p[i]=mid,l=mid+1;
			else    r=mid-1;
		}
		p[i]=min(p[i],m-1);
	}
	for(int i=n;i>=1;i--)
	{
		if(a[i]!=b[m])  continue;
		int l=1,r=min(i,m);
		while(l<=r)//同理找后缀
		{
			int mid=(l+r)/2;
			if(Hash1[i]-Hash1[i-mid]*mul[mid]==Hash2[m]-Hash2[m-mid]*mul[mid])  q[i]=mid,l=mid+1;
			else    r=mid-1;
		}
		q[i]=min(q[i],m-1);
	}
	long long res=0;
	for(int i=1;i<=n-m+1;i++)
	{
		if(Hash1[i+m-1]-Hash1[i-1]*mul[m]==Hash2[m])    res+=solve(i-1)+solve(n-i-m+1);//第一种情况
	}
	if(q[n])	change_tree(1,1,m-1,q[n]);
	for(int i=n-m;i>=1;i--)//注意是逆序！！！！
	{
		if(p[i])	res+=Q(m-1,m-p[i],m-1,0)+Q(m-1,m-p[i],m-1,1)*(p[i]-m+1);
		if(q[i+m-1])	change_tree(1,1,m-1,q[i+m-1]);//每次要记得更新线段树
	}
	cout<<res;
	return 0;
}