浙大《数据结构》第八章：图(下)

注：本文使用的网课资源为中国大学MOOC

https://www.icourse163.org/course/ZJU-93001

最小生成树问题
拓扑排序
关键路径问题

最小生成树问题

村村通中，修路用最少的边连通起来，这样更省钱。

什么是最小生成树(minimum spanning tree)

1、是一个树

无回路
|V|个顶点一定有|V|-1条边

2、是生成树

包含全部顶点
|V|-1条边都在图里
向生成树中任意加一条边都构成回路

3、边的权重最小

4、最小生成树存在 \(\longleftrightarrow\)图连通

贪心算法

什么是贪：每一步都要最好的

什么是“好”：权重最小的边

需要约束：

只能用图里有的边
只能正好用掉|V|-1条边
不能有回路

Prim算法——让一棵小树长大

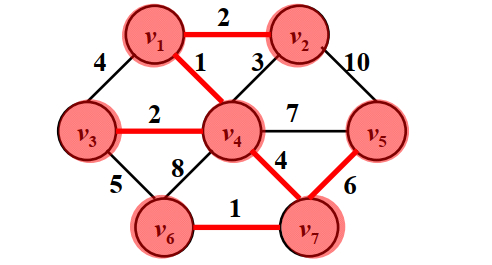
算法描述：

首先选择v1作为起始点，作为树，查找v1相关的边，选择其中权重最小的一条边，即<v1,v4>.
此时树长大了一点，有v1,v4两个顶点，继续查找与树相关的边，选择其中权重最小的边，此时有<v1,v2>,<v3,v4>可选，此时选择编号较小的v2加入树
此时树有v1,v4,v2三个顶点，继续查找与之相关，但是权重最小的边，由于<v2,v4>或者<v1,v4>连通后会产生回路，因此此时需要选择<v4,v7>
此时树中有v1,v4,v2,v3,v7,根据查找法则，选择<v6,v7>
此时树中有v1,v4,v2,v3,v7,v6,由于<v3,v6>连通后会产生回路，此时选择<v5,v7>
此时树的所有顶点均被收录，收录顺序为v1,v4,v2,v3,v7,v6,v5

伪代码

void Prim()
{
    MST = {s};
    while (1)
    {
        V = 未收录顶点中dist最小者;
        if ( 这样的V不存在 )
            break;
        将V收录进MST: dist[V]=0;
        for ( V的每一个邻接点W)
            if ( dist[W] !=0 )
                if ( E(v,w) < dist[W] )
                {
                    dist[W] = E(V,W);
                    parent[W] = V;
                }
    }
    if ( MST中收到顶点不到|V|个) // 剩下的顶点与树不相关，图不连通
        Error( "生成树不存在");
}

注意

dist[V]应该初始化为E(s,V)或者无穷大

parent[V]=-1

时间复杂度是\(T=O(V^2)\)，因此Prim算法更适用于稠密图

程序实现

#include <iostream>
#include <vector>     /*调用动态数组*/

/***************************vector的常用操作*********************/
/* push_back(t) 在数组的最后添加一个值为t的数据
   size() 当前使用数据的大小
   pop_back(); // 弹出容器中最后一个元素（容器必须非空）
   back(); // 返回容器中最后一个元素的引用                        */
/***************************************************************/
using namespace std;

#define INF 100000
#define MaxVertex 105
typedef int Vertex;

/*****************************全局变量***************************/
int G[MaxVertex][MaxVertex]; //邻接矩阵
int parent[MaxVertex];       // 并查集
int dist[MaxVertex];         // 距离
int Nv;                      // 结点数
int Ne;                      // 边
int sum;                     // 权重和
vector<Vertex> MST;          // 最小生成树

/*****************************函数声明****************************/
Vertex FindMin(void); // 查找未收录中dist最小的点
void Prim(Vertex s);  // 以s为起点的prim算法

/****************************************************************/
/*                             主函数                            */
/****************************************************************/
int main()
{
    Vertex v1, v2;
    int weight;
    sum = 0; // 权重和初始化为0

    // 输入图的顶点数和边数，初始化图
    cin >> Nv >> Ne;
    for (int i = 1; i <= Nv; i++)
    {
        for (int j = 1; j <= Nv; j++)
            G[i][j] = 0; // 初始化图
        dist[i] = INF;   // 初始化距离
        parent[i] = -1;  // 初始化并查集
    }
    // 初始化点
    for (int i = 0; i < Ne; i++)
    {
        cin >> v1 >> v2 >> weight;
        G[v1][v2] = weight;
        G[v2][v1] = weight;
    } 

    // 选择顶点1为源点, 运行prim算法
    Prim(1);

    // 输出算法运行结果
    cout << "被收录顺序：" << endl;
    for (int i = 0; i < Nv; i++)
        cout << MST[i] << " ";
    cout << "权重和为：" << sum << endl;
    cout << "该生成树顶点为：" << endl;
    // 因为顶点1为源点，这里直接从顶点2开始输出
    for (Vertex i = 2; i <= Nv; i++)
        cout << parent[i] << " ";
    
    system("pause"); //程序暂停，显示按下任意键继续
    return 0;
}

/*****************************函数定义****************************/
// 查找未收录中dist最小的点
Vertex FindMin()
{
    int min = INF;
    Vertex xb = -1;
    // 在未被收录的结点中遍历
    for (Vertex i = 1; i <= Nv; i++)
        if (dist[i] && dist[i] < min) // dist=0代表已被收录
        {
            min = dist[i];
            xb = i;
        }
    return xb;
}

// 以s为起点的prim算法
void Prim(Vertex s)
{
    dist[s] = 0;      // 将起点的dist赋值为0
    MST.push_back(s); // 将起点s压入栈中
    for (Vertex i = 1; i <= Nv; i++)
    {
        if ( G[s][i] ) // 遍历与s相关的边
        {
            dist[i] = G[s][i];  // dist由正无穷赋值为边权重
            parent[i] = s;      // parent赋值为s
        }
    }

    while (1)
    {
        Vertex v = FindMin(); //查找未收录中dist最小的点 
        if (v == -1) 
            break;
        sum += dist[v];
        dist[v] = 0;          // dist=0,可以视为将V收录进MST的标志
        MST.push_back(v);     // 将找到的最小权重顶点压入MST
        for (Vertex w = 1; w <= Nv; w++) // 对于当前顶点的每个邻接点
            if (G[v][w] && dist[w])      // 如果邻接点未被收录,也可判断是否会形成回路
                if (G[v][w] < dist[w])   // 而且邻接点有边
                {
                    dist[w] = G[v][w];   // 更新其邻接点dist为边的权重
                    parent[w] = v;       // parent为该顶点
                }
    }
}

图示的测试数据

Kruskal算法,将森林合并成树

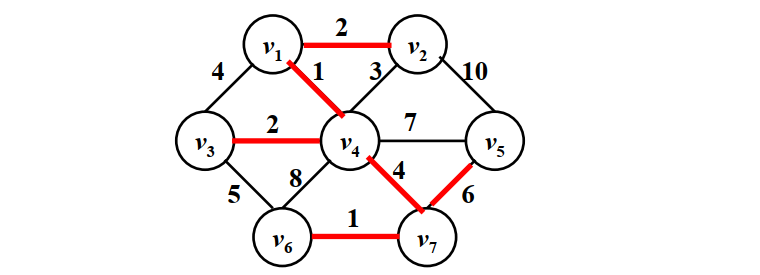
算法描述

在初始情况下，认为每个顶点都是一棵树，每次找权重最小的边，然后通过找边，把所有的树都合并进来，直到所有的顶点都并成一棵树
首先收集的边是权重为1的<v1,v4>和<v6,v7>,此时包含4个顶点
然后收集权重为2的边<v3,v4>和<v1,v2>，此时包含v1,v4,v6,v7,v3,v2一共6个顶点
接下来由于权重为4的<v1,v3>和权重为5的边<v3,v6>连接后，会产生回路，因此收集权重为6的边<v7,v5>
此时已经收录了6条边，代表所有的顶点均已被收录

伪代码

void Kruskal ( Graph G )
{
    MST = {};
    while ( MST 中不到 |V| -1 条边 && E 中还有边 )
    {
        从E中取出一条权重最小的边E(v,w);  // 可利用最小堆实现
        将E(v,w)从E中删除；
        if ( E(v,w)在MST中不构成回路 ) // 可利用并查集的查找实现
            将E(v,w)加入MST;
        else
            彻底无视E(v,w);
    }
    if ( MST中不到|V|-1条边 ) // 等价于此图是不连通的
        Error ("生成树不存在");
}

注意

Kruskal更适用于稀疏图，即边的条数较少差不多和顶点的数量是一个数量级

算法的时间复杂度\(T=O(|E|log|E|)\)

程序实现

注: 测试样例与prim算法测试数据一致

#include <stdio.h>
#include <stdlib.h>  //调用malloc()和free()
#include <WinDef.h>
#include <windows.h> //windows.h里定义了关于创建窗口，消息循环等函数S


/*****************************全局变量***************************/
#define MaxVertexNum 105
typedef int Vertex;
typedef Vertex SetName;            /* 默认用根结点的下标作为集合名称 */
typedef int SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */
typedef int WeightType;            /* 边的权值设为整型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1, V2;     // 有向边<V1, V2> /
    WeightType Weight; // 权重
};
typedef PtrToENode Edge;

SetType VSet;           /* 结点数组 */
Edge ESet;              /* 边数组 */

/*****************************函数声明****************************/
// 并查集相关函数
void InitializeVSet(int N);                      // 初始化并查集
void SetUnion(Vertex Root1, Vertex Root2);       // 集合合并
Vertex Find(Vertex V);                           // 找到集合的根
int CheckCycle(Vertex V1, Vertex V2);            // 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路
// 最小堆相关函数
void MinHeap(int i, int M);   // 将M个元素的数组中以ESet[i]为根的子堆调整为最小堆
void InitializeESet(int M);   // 初始化最小堆
int GetEdge(int CurrentSize); // 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆

int Kruskal(int N, int M);
/****************************************************************/
/*                             主函数                            */
/****************************************************************/
int main()
{
    int N, M, i;

    scanf("%d %d", &N, &M);
    if (M < N - 1) /* 太少边肯定不可能连通 */
        printf("-1\n");
    else
    {
        ESet = (Edge)malloc(sizeof(struct ENode) * M);
        for (i = 0; i < M; i++)
            scanf("%d %d %d", &ESet[i].V1, &ESet[i].V2, &ESet[i].Weight);
        printf("%d\n", Kruskal(N, M));
    }

    system("pause"); //程序暂停，显示按下任意键继续
    return 0;
}


/*****************************函数定义****************************/
/*---------- 结点并查集相关函数 ----------*/
void InitializeVSet(int N)
{ /* 并查集初始化 */
    while (N)
        VSet[N--] = -1;
}

/* 查找V所在的集合 */
Vertex Find(Vertex V)
{ 
    Vertex root, trail, lead;

    for (root = V; VSet[root] > 0; root = VSet[root])
        ; /* 查找V所在集合的根root */
    for (trail = V; trail != root; trail = lead)
    {
        lead = VSet[trail];
        VSet[trail] = root;
    } /* 路径压缩 */
    return root;
}

/*按规模求并，把小集合并入大集合 */
void SetUnion(Vertex Root1, Vertex Root2)
{ 
    /* 这里保证Root1和Root2都是集合的根 */
    if (VSet[Root2] < VSet[Root1])
    {                               /* 如果Root1比较大 */
        VSet[Root2] += VSet[Root1]; /* Root1并入Root2 */
        VSet[Root1] = Root2;
    }
    else
    {                               /* 如果Root2比较大 */
        VSet[Root1] += VSet[Root2]; /* Root2并入Root1 */
        VSet[Root2] = Root1;
    }
}
/*------------------------------------------*/
/*----------- 边的最小堆相关函数 -----------*/
/* 将M个元素的数组中以ESet[i]为根的子堆调整为最小堆 */
void MinHeap(int i, int M)
{ 
    int child;
    struct ENode temp;

    temp = ESet[i];
    for (; ((i << 1) + 1) < M; i = child)
    {
        child = (i << 1) + 1;
        if (child != M - 1 && ESet[child + 1].Weight < ESet[child].Weight)
            child++;
        if (temp.Weight > ESet[child].Weight)
            ESet[i] = ESet[child];
        else
            break;
    }
    ESet[i] = temp;
}

/* 初始化最小堆 */
void InitializeESet(int M)
{ 
    int i;
    for (i = M / 2; i >= 0; i--)
        MinHeap(i, M);
}

/* 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆 */
int GetEdge(int CurrentSize)
{ 
    struct ENode temp;

    /* 将最小边与当前堆的最后一个位置的边交换 */
    temp = ESet[0];
    ESet[0] = ESet[CurrentSize - 1];
    ESet[CurrentSize - 1] = temp;
    /* 将剩下的边继续调整成最小堆 */
    MinHeap(0, CurrentSize - 1);
    return CurrentSize - 1; /* 返回最小边所在位置 */
}
/*------------------------------------------*/

/* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
int CheckCycle(Vertex V1, Vertex V2)
{                            
    Vertex Root1 = Find(V1); /* 得到V1所属的连通集名称 */
    Vertex Root2 = Find(V2); /* 得到V2所属的连通集名称 */

    if (Root1 == Root2) /* 若V1和V2已经连通，则该边不能要，返回0 */
        return 0;
    else
    { /* 否则该边可以被收集，同时将V1和V2并入同一连通集 */
        SetUnion(Root1, Root2);
        return 1;
    }
}

/* 给定结点和边的数目，返回最小生成树总权重 */
int Kruskal(int N, int M)
{                     
    int EdgeN = 0;    /* 生成树边集合计数器 */
    int Cost = 0;     /* 最小生成树权重累计 */
    int NextEdge = M; /* 下一个最小权重边的位置，初始化为总边数 */

    InitializeVSet(N); /* 初始化结点并查集VSet */
    InitializeESet(M); /* 根据边的权重建立最小堆ESet */
    while (EdgeN < N - 1)
    {                      /* 当收集的边不足以构成树时 */
        if (NextEdge <= 0) /* 边集已空 */
            break;
        NextEdge = GetEdge(NextEdge); /* 从边集中得到最小边的位置 */
        if (CheckCycle(ESet[NextEdge].V1, ESet[NextEdge].V2))
        {
            /* 如果该边的加入不构成回路，即两端结点不属于同一连通集 */
            Cost += ESet[NextEdge].Weight; /* 收入该边，累计权重 */
            EdgeN++;                  /* 生成树中边数加1 */
        }
    }
    if (EdgeN < N - 1)
        Cost = -1; /* 若收集的边不足以构成树，设置信号 */
    return Cost;
}

拓扑排序

拓扑序：如果途中从v到w有一条有向路径，则v一定排在w之前，满足此条件的顶点序列成为一个拓扑序
获得一个拓扑序的过程就是拓扑排序
网络(AOV)如果有合理的拓扑序，则必定是有向无环图(Direceted Acyclic Graph, DAG)

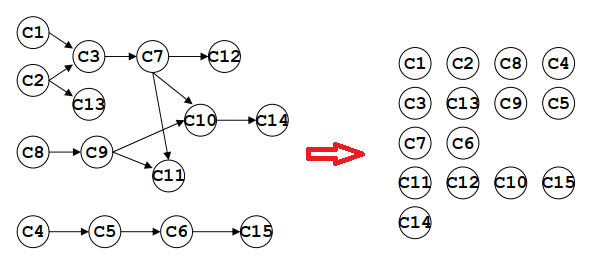
算法描述

如上图图所示，图中的顶点代表活动，图中的有向边代表活动的先后关系；通过拓扑排序，可以将左侧图以右侧的表示的顺序输出。

首先将每个点的度进行存储；
遍历其中度为0的点，并入队，然后删除所有去该顶点的边
开始弹出队列，并且遍历该点的邻接点，判断是否入度为0，若为0，则将邻接点入队
如此循环，直到每个点都弹出队列

伪代码

void TopSort()
{
    for ( 图中每一个顶点V )
        if ( Indegree[V]==0 )
            Enqueue(V,Q)
    while ( !IsEmpty(Q) )
    {
        V = Dequeue( Q );
        输出V，或者记录V的输出序号;
        cnt++;
        for ( V的每个邻接点W)
            if ( --Indegree[W]==0 )
                Enqueue( W,Q );
    }
    if ( cnt != |V| )
        Error("图中有回路")
}

注意

此算法可以用来检测有向图是否DAG
算法的时间复杂度\(T=O(|V|+|E|)\)
排序并不是唯一的，可能存在是并列关系而不在同一集合的点。

程序实现

/* 邻接表存储 - 拓扑排序算法 */

#include <iostream> /* 引入命名空间，以及模块化I/O */
#include <queue>    /* 引用队列，常用函数有empty，push，front，back，pop，size */
#include <stdio.h>
#include <stdlib.h>
using namespace std;

/*****************************全局变量***************************/
#define MaxVertexNum 105
typedef int Vertex;
typedef Vertex SetName;            /* 默认用根结点的下标作为集合名称 */
typedef int SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */
typedef int WeightType;            /* 边的权值设为整型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1, V2;     // 有向边<V1, V2> 
    WeightType Weight; // 权重
};
typedef PtrToENode Edge;

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
    Vertex AdjV;        // 邻接点下标
    WeightType Weight;  // 权重
    PtrToAdjVNode Next; // 指向下一个邻接点的指针
};

/* 顶点表头结点的定义 */
typedef struct Vnode
{
    PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum];     /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv;    // 顶点数
    int Ne;    // 边数
    AdjList G; // 邻接表
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

/*****************************函数声明****************************/
LGraph CreateGraph(int VertexNum);     // 初始化一个有VertexNum个顶点但没有边的图
void InsertEdge(LGraph Graph, Edge E); // 插入边
void printG(LGraph Graph);             // 打印图
bool TopSort(LGraph Graph, Vertex TopOrder[]); //拓扑排序



/****************************************************************/
/*                             主函数                            */
/****************************************************************/
int main()
{
    LGraph ListGraph;
    Vertex TopOrder[MaxVertexNum];

    Edge E;
    Vertex V;
    int Nv, i;
    // 读入顶点个数
    scanf("%d", &Nv);        
    ListGraph = CreateGraph(Nv); // 初始化有Nv个顶点但没有边的图
    // 读入边数
    scanf("%d", &(ListGraph->Ne)); 
    if (ListGraph->Ne != 0)
    {
        /* 如果有边 */
        E = (Edge)malloc(sizeof(struct ENode)); // 建立边结点
        /* 读入边，格式为"起点 终点 权重"，插入邻接表 */
        for (i = 0; i < ListGraph->Ne; i++)
        {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge(ListGraph, E);
        }
    }
    
    // 打印邻接表
    printG(ListGraph);

    // 拓扑排序，并输出拓扑序
    if ( TopSort(ListGraph, TopOrder) )
    {
        printf("topSort is : ");
        for (i = 0; i < Nv; i++)
            printf("%d ", TopOrder[i]);
        printf("\n ");
    }
        

    system("pause"); //程序暂停，显示按下任意键继续
    return 0;
}

/* 初始化一个有VertexNum个顶点但没有边的图 */
LGraph CreateGraph(int VertexNum)
{
    Vertex V, W;
    LGraph Graph;

    Graph = (LGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;

    /* 注意：这里默认顶点编号从1开始，到(Graph->Nv) */
    for (V = 1; V <= Graph->Nv; V++)
        Graph->G[V].FirstEdge = NULL;

    return Graph;
}
/* 向LGraph中插入边 */
void InsertEdge(LGraph Graph, Edge E)
{
    PtrToAdjVNode NewNode;

    /***************** 插入边 <V1, V2> ****************/
    /* 为V2建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;

    /********** 若是无向图，还要插入边 <V2, V1> **********/
    /* 为V1建立新的邻接点 */
    //NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    //NewNode->AdjV = E->V1;
    //NewNode->Weight = E->Weight;
    /* 将V1插入V2的表头 */
    //NewNode->Next = Graph->G[E->V2].FirstEdge;
    //Graph->G[E->V2].FirstEdge = NewNode;
}

// 打印
void printG(LGraph Graph)
{
    Vertex v;
    PtrToAdjVNode tmp;
    printf("Lgraph output:\n");
    for (v = 1; v <= Graph->Nv; v++)
    {
        tmp = Graph->G[v].FirstEdge;
        printf("%d ", v);
        while (tmp)
        {
            printf("->%d ", tmp->AdjV);
            tmp = tmp->Next;
        }
        printf("\n");
    }
}

/* 对Graph进行拓扑排序,  TopOrder[]顺序存储排序后的顶点下标 */
bool TopSort(LGraph Graph, Vertex TopOrder[])
{ 
    int Indegree[MaxVertexNum], cnt;
    Vertex V;
    PtrToAdjVNode W;
    queue<int> Q; // 定义队列Q
    //Queue Q = CreateQueue(Graph->Nv);

    /* 初始化Indegree[] */
    for (V = 1; V <= Graph->Nv; V++)
        Indegree[V] = 0;

    /* 遍历图，得到Indegree[] */
    for (V = 1; V <= Graph->Nv; V++)
        for (W = Graph->G[V].FirstEdge; W; W = W->Next)
            Indegree[W->AdjV]++; /* 对有向边<V, W->AdjV>累计终点的入度 */

    /* 将所有入度为0的顶点入列 */
    for (V = 1; V <= Graph->Nv; V++)
        if (Indegree[V] == 0)
            Q.push(V);
            //AddQ(Q, V);

    /* 下面进入拓扑排序 */
    cnt = 0;
    while ( !Q.empty() )
    {
        //V = DeleteQ(Q);      /* 弹出一个入度为0的顶点 */
        V = Q.front();
        Q.pop();
        TopOrder[cnt++] = V; /* 将之存为结果序列的下一个元素 */
        /* 对V的每个邻接点W->AdjV */
        for (W = Graph->G[V].FirstEdge; W; W = W->Next)
            if (--Indegree[W->AdjV] == 0) /* 若删除V使得W->AdjV入度为0 */
                Q.push(W->AdjV);
                //AddQ(Q, W->AdjV);         /* 则该顶点入列 */
    }/* while结束*/

    if (cnt != Graph->Nv)
        return false; /* 说明图中有回路, 返回不成功标志 */
    else
        return true;
}

图示的测试样例

关键路径问题

由绝对不允许延误的活动组成的路径，一般取决于信号所经过的延时最大路径
AOE(activity on edge)网络：一般用于安排项目的工序
可以解决的问题
1. 所用时长最短的方案
2. 机动时间是哪几个工序
3. 所用时长最长的方案

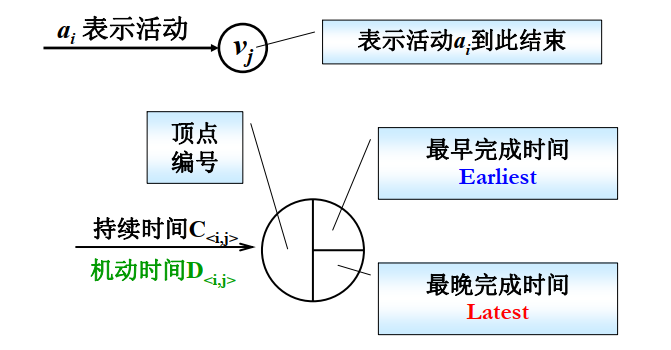
假设开始点是v1, 从v1到vi的最长路径长度叫做事件vi的最早发生时间
这里用Earlist[i]表示事件a[i]开始的最早时间，Latest[i]为该事件开始的最晚时间
而关键路径就是那些没有机动时间的边组成的路径

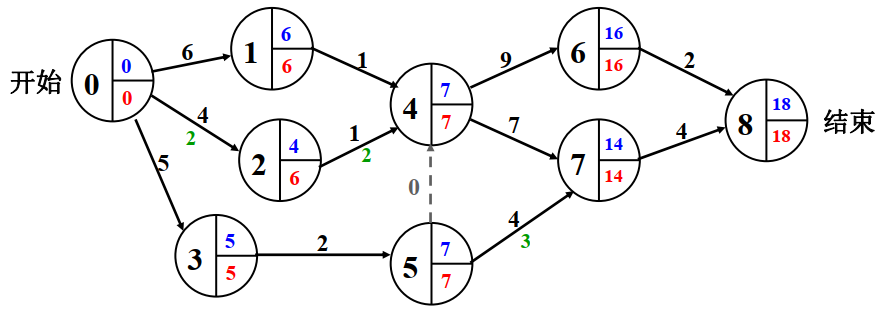
算法描述

以活动0为起始点(入度为0的点)，到活动1的距离为C<0,1>=6，因此Earlist[1]=6,同理可得Earlist[2]=4，Earlist[3]=5，Earlist[5]=7
对于活动4，同时受活动1，2的影响，但是需要等到活动1完成，再加上C<1,4>才能得到最早完成时间Earlist[4] = max{Earlist[1]+C<1,4>, Earlist[2]+C<2,4>, Earlist[5]+C<5,4>}。
同理可得Earlist[6]=16，Earlist[7]=14，Earlist[8]=18
从最后一个活动(出度为0的点)往回推可以得到Latest的值，此时Latest[8]=Earlist[8]=18
而活动6,7由于回推只与活动8有关，Latest[6]=16，Latest[7]=14
对于活动4，其同时影响活动6和活动7，因此对其最晚活动时间Latest[4]=min{Latest[6]-C<6,4>, Latest[7]-C<7,4>},同理Latest[5]=min
同理可以得到Latest[1]=6,Latest[2]=6, Latest[3]=5,Latest[0]=0
最后机动时间取决于两个活动之间最晚完成与最早完成时间的差值

公式总结

\(Earliest[j] = \max_{<i,j> \in E}\{ Earliest[i] + C_{<i,j>}\}\)
\(Latest[j] = \min_{<i,j> \in E}\{ Latestest[i] - C_{<i,j>}\}\)
\(D_{<i,j>}=Latest[j]-Earliest[i]-C_{<i,j>}\)

程序实现

/* 邻接表存储 - 关键路径算法 */

#include <iostream> /* 引入命名空间，以及模块化I/O */
#include <queue>    /* 引用队列，常用函数有empty，push，front，back，pop，size */
#include <stdio.h>
#include <stdlib.h>
using namespace std;

/*****************************全局变量***************************/
#define MaxVertexNum 105
typedef int Vertex;
typedef Vertex SetName;            /* 默认用根结点的下标作为集合名称 */
typedef int SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */
typedef int WeightType;            /* 边的权值设为整型 */

// 全局数组存储拓扑序
Vertex TopOrder[MaxVertexNum];

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1, V2;     // 有向边<V1, V2>
    WeightType Weight; // 权重
};
typedef PtrToENode Edge;

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
    Vertex AdjV;        // 邻接点下标
    WeightType Weight;  // 权重
    PtrToAdjVNode Next; // 指向下一个邻接点的指针
};

/* 顶点表头结点的定义 */
typedef struct Vnode
{
    PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum];     /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv;    // 顶点数
    int Ne;    // 边数
    AdjList G; // 邻接表
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

/*****************************函数声明****************************/
LGraph CreateGraph(int VertexNum);                     // 初始化一个有VertexNum个顶点但没有边的图
void InsertEdge(LGraph Graph, Edge E);                 // 插入边
void printG(LGraph Graph);                             // 打印图
bool TopSort(LGraph Graph, int *pEtv);                 // 拓扑排序
void CriticalPath(LGraph Graph, int *pEtv, int *pLtv); // 求关键路径
/****************************************************************/
/*                             主函数                            */
/****************************************************************/
int main()
{
    LGraph ListGraph;
    Vertex *TopOrdered = new Vertex[MaxVertexNum]; // 拓扑序存储数组
    int *pEtv = new int[MaxVertexNum];    // 最早完成时间的存储数组
    int *pLtv = new int[MaxVertexNum];    // 最晚完成时间的存储数组
    
    Edge E;
    Vertex V;
    int Nv, i;
    // 读入顶点个数
    scanf("%d", &Nv);
    ListGraph = CreateGraph(Nv); // 初始化有Nv个顶点但没有边的图
    // 读入边数
    scanf("%d", &(ListGraph->Ne));
    if (ListGraph->Ne != 0)
    {
        /* 如果有边 */
        E = (Edge)malloc(sizeof(struct ENode)); // 建立边结点
        /* 读入边，格式为"起点 终点 权重"，插入邻接表 */
        for (i = 0; i < ListGraph->Ne; i++)
        {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge(ListGraph, E);
        }
    }

    // 打印邻接表
    printG(ListGraph);

    // 拓扑排序，并输出拓扑序
    if ( TopSort(ListGraph, pEtv) )
    {
        printf("topSort is :");
        // 1、打印拓扑序
        for (i = 0; i < Nv; i++)
            printf(" %d", TopOrder[i]);
        printf("\n");
        // 2、打印最早完成时间
        printf("Earilest time is :");
        for (i = 0; i < Nv; i++)
            printf(" %d", pEtv[i]);
        printf("\n");
        // 求关键路径
        printf("Non-emergency is :");
        CriticalPath(ListGraph, pEtv, pLtv);
    }

    system("pause"); //程序暂停，显示按下任意键继续
    return 0;
}

/* 初始化一个有VertexNum个顶点但没有边的图 */
LGraph CreateGraph(int VertexNum)
{
    Vertex V, W;
    LGraph Graph;

    Graph = (LGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;

    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv-1) */
    for (V = 0; V < Graph->Nv; V++)
        Graph->G[V].FirstEdge = NULL;

    return Graph;
}
/* 向LGraph中插入边 */
void InsertEdge(LGraph Graph, Edge E)
{
    PtrToAdjVNode NewNode;

    /***************** 插入边 <V1, V2> ****************/
    /* 为V2建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;

    /********** 若是无向图，还要插入边 <V2, V1> **********/
    /* 为V1建立新的邻接点 */
    //NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    //NewNode->AdjV = E->V1;
    //NewNode->Weight = E->Weight;
    /* 将V1插入V2的表头 */
    //NewNode->Next = Graph->G[E->V2].FirstEdge;
    //Graph->G[E->V2].FirstEdge = NewNode;
}

// 打印
void printG(LGraph Graph)
{
    Vertex v;
    PtrToAdjVNode tmp;
    printf("Lgraph output:\n");
    for (v = 0; v < Graph->Nv; v++)
    {
        tmp = Graph->G[v].FirstEdge;
        printf("%d ", v);
        while (tmp)
        {
            printf("->%d ", tmp->AdjV);
            tmp = tmp->Next;
        }
        printf("\n");
    }
}

/* 对Graph进行拓扑排序,  TopOrder顺序存储排序后的顶点下标, pEtv存储最早完成时间 */
bool TopSort(LGraph Graph, int *pEtv)
{
    int Indegree[MaxVertexNum], cnt;
    Vertex V;
    PtrToAdjVNode W;
    queue<int> Q; // 定义队列Q

    /* 初始化Indegree[]和pEtv */
    for (V = 0; V < Graph->Nv; V++)
    {
        Indegree[V] = 0;
        pEtv[V] = 0;
    }
        
    /* 遍历图，得到Indegree[] */
    for (V = 0; V < Graph->Nv; V++)
        for (W = Graph->G[V].FirstEdge; W; W = W->Next)
            Indegree[W->AdjV]++; /* 对有向边<V, W->AdjV>累计终点的入度 */

    /* 将所有入度为0的顶点入列 */
    for (V = 0; V < Graph->Nv; V++)
        if (Indegree[V] == 0)
            Q.push(V);

    /* 下面进入拓扑排序 */
    cnt = 0;
    while (!Q.empty())
    {
        V = Q.front();
        Q.pop();             /* 弹出一个入度为0的顶点 */
        TopOrder[cnt++] = V; /* 将之存为结果序列的下一个元素 */
        /* 对V的每个邻接点W->AdjV */
        for (W = Graph->G[V].FirstEdge; W; W = W->Next)
        {
            if (--Indegree[W->AdjV] == 0) /* 若删除V使得W->AdjV入度为0 */
                Q.push(W->AdjV);          /* 则该顶点入列 */
            if (pEtv[V] + W->Weight > pEtv[W->AdjV])
                // pEtv[W]  = max(取V的临边权重 + pEtv[V]);
                pEtv[W->AdjV] = pEtv[V] + W->Weight;
        }      
    } /* while结束*/

    if (cnt != Graph->Nv)
        return false; /* 说明图中有回路, 返回不成功标志 */
    else
        return true;
}

// 关键路径
void CriticalPath(LGraph Graph, int *pEtv, int *pLtv)
{
    // pEtv  事件最早发生时间
    // PLtv  事件最迟发生时间
    Vertex V, K;
    PtrToAdjVNode W = NULL;
    int ete = 0, lte = 0; // 声明活动最早发生时间和最迟发生时间变量
    // pLtv初始化
    for (V = 0; V < Graph->Nv; V++)
    {
        pLtv[V] = pEtv[Graph->Nv -1]; 
    }
    // 逆向求出各顶点的最晚完成时间
    for (V = 0; V < Graph->Nv; V++)
    {
        K = TopOrder[Graph->Nv - 1 - V]; // 拓扑序逆向输出顶点序号
        for (W = Graph->G[K].FirstEdge; W; W = W->Next) // 遍历其邻接点
        {

            if (pLtv[W->AdjV] - W->Weight < pLtv[K])
                // // pLtv[W]  = min(取V的临边权重 + pEtv[V]);
                pLtv[K] = pLtv[W->AdjV] - W->Weight;
        }
    }
    // 求 ete, lte, 和关键路径
    for (V = 0; V < Graph->Nv; V++)
    {
        W = Graph->G[V].FirstEdge; // 遍历V顶点的邻接点
        while (W != NULL)
        {
            ete = pEtv[V];                   // 活动最早发生时间
            lte = pLtv[W->AdjV] - W->Weight; // 活动最迟发生时间
            if (ete != lte)
                printf(" <%d,%d>", V, W->AdjV);
            W = W->Next;           
        }
    }
    printf("\n");
}

图示的测试样例

posted @ 2020-04-09 21:41 Super_orange 阅读(279) 评论(0) 编辑收藏举报

刷新页面返回顶部

橙子不好笑

浙大《数据结构》第八章：图(下)

最小生成树问题

什么是最小生成树(minimum spanning tree)

贪心算法

Prim算法——让一棵小树长大

Kruskal算法,将森林合并成树

拓扑排序

关键路径问题

公告