Relation-Shape Convolutional Neural Network for Point Cloud Analysis(CVPR 2019)

代码：https://github.com/Yochengliu/Relation-Shape-CNN

文章：https://arxiv.org/abs/1904.07601

作者直播:https://www.bilibili.com/video/av61824733

作者维护了一个收集一系列点云论文、代码、数据集的github仓库:https://github.com/Yochengliu/awesome-point-cloud-analysis

这篇paper是CVPR 2019 Oral & Best paper finalist

Abstract & Introduction

在点云中，由于不规则点中隐含的形状很难捕捉，使得点云分析非常具有挑战性。在本文中，作者针对点云数据提出了RS-CNN，即Relation-Shape Convolutional Neural Network，其核心思想是从几何拓扑中学习点云关系信息。RS-CNN在多个数据集中都取得了SOTA的表现。
主要贡献如下：

• 提出了一种新型的从关系中学习的卷积算子关系形状卷积。它可以显式地对点的几何关系进行编码，从而在很大程度上提高了对形状的感知能力和鲁棒性。即，RS-Conv
• 提出一个具有关系形状卷积的深层层次结构，即，RS-CNN。将规则网格CNN扩展到不规则配置，实现点云的上下文形状感知学习。即，基于RS-Conv设计的RS-CNN
• 在三个任务中对具有挑战性的基准进行广泛的实验，以及深入的经验和理论分析，证明RS-CNN达到了SOTA的水平。即，精度高效果好（modelnet40 93.6）

Shape-Aware Representation Learning

首先，作者归纳了一个通用的卷积公式

\[f_{P_{sub}}=\sigma(\mathcal{A}(\{\tau(f_{x_{j}}),\forall x_j\})),d_{ij}<r\forall(x_j) \in \mathcal{N}(x_i) \]

其中，\(x\)表示3D点，\(f_{x_j}\)表示\({x_j}\)的特征向量，\(d_{ij}\)是\(x_i\)和\(x_j\)之间的欧式距离Euclidean distance，\(\tau\)用于转化单点特征，\(\mathcal{A}\)表示聚合函数，\(\sigma\)为激活函数。在这个公式中，\(\mathcal{A}\)和\(\tau\)的定义很关键，也就是这篇paper的创新所在。

首先，如果将这个公式套用在2D图像当中，则\(\tau(f_{x_{j}})=W_j \cdot f_{x_j}\),其中\(w_j\)为learnable weight（可以理解为卷积核），“\(\cdot\)”表示点乘，\(\mathcal{A}\)表示求和，其实就是一个卷积操作。而传统卷积有两个问题，1是不具备置换不变性，2是没有学习到形状信息。因此，作者对\(\mathcal{A}\)和\(\tau\)进行了修改，使其处理点云信息时，具有置换不变性，以及能够学习到形状信息。置换不变性在pointnet中已经实现，就是用max来表示\(\mathcal{A}\)，那么剩下的就是学习形状信息，那么如何学习形状信息?就是通过这个\(\tau\)实现的。
为了捕获形状信息（或者关系信息），作者将\(\tau\)定义为：

\[\tau(f_{x_{j}})=W_{ij} \cdot f_{x_j}=\mathcal{M}(h_{ij})\cdot f_{x_j} \]

\(\mathcal{M}\)用于将两个点的关系映射为high-level的信息（\(\mathcal{M}\)实际上就是MLP，将低维特征映射成高维特征，而低维特征就是点的位置关系，比如两个点间的距离，相对坐标等），而\(h_{ij}\)就是低维特征。
RS-Conv的流程图如下：

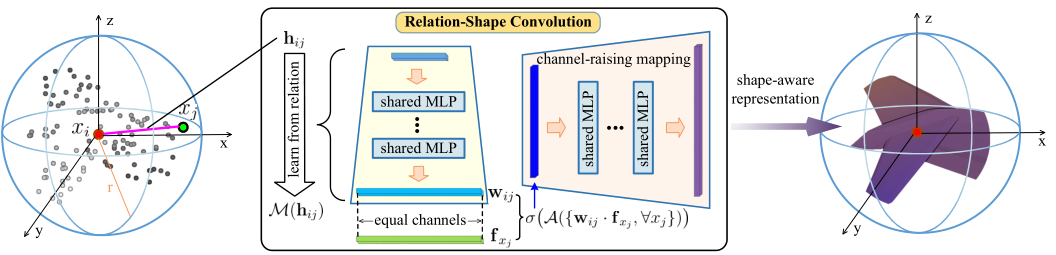
1. 首先通过FPS进行采样，得到质心\(X_i\)
2. 在球形领域寻找近邻，\(X_j\)
3. 对于每个邻居点j，计算j和i的low-level信息，即\(h_{ij}\)，\(h_{ij}\)的表示方法很多，作者在论文中将其定义为\(h_{ij}=[3D-Ed,x_i-x_j,x_i,x_j]\)，即将两点间的欧式距离(1维)，相对坐标(3维)，i的坐标(3维)和j的坐标(3维)进行拼接，得到一个10维的low-level信息。
4. 使用MLP将\(h_{ij}\)映射成高维信息，即\(\mathcal{M}(h_{ij})\)，得到\(W_{ij}\)，注意，这边映射成高维信息的\(W_{ij}\)的维度要和\(f_{x_j}\)的特征维度相同，才可以进行点乘操作
5. 将得到的\(W_{ij}\)和\(f_{x_j}\)进行点乘。
6. max操作，聚合所有近邻的信息作为质心\(x_i\)的新特征，接着为了实现更强大的形状感知表示，将\(x_i\)进行进一步的通道提升映射。即上图中的channel-raising mapping

以上就是RS-Conv的操作过程。有点复杂，类比成2D图像的卷积的话，一个明显的区别是RS-Conv的卷积核\(W_{ij}\)是通过\(h_{ij}\)（即低维关系信息）学习来的，这也是本文的最大创新点，但实际上，这个操作在其他论文中也有出现，比如GACnet，DGCNN只是他们定义\(h_{ij}\)的方式不同。
网络结构如下

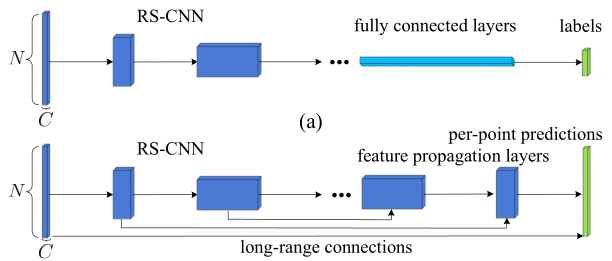
比较简单，不赘述，具体如何实现需要看代码。

实验

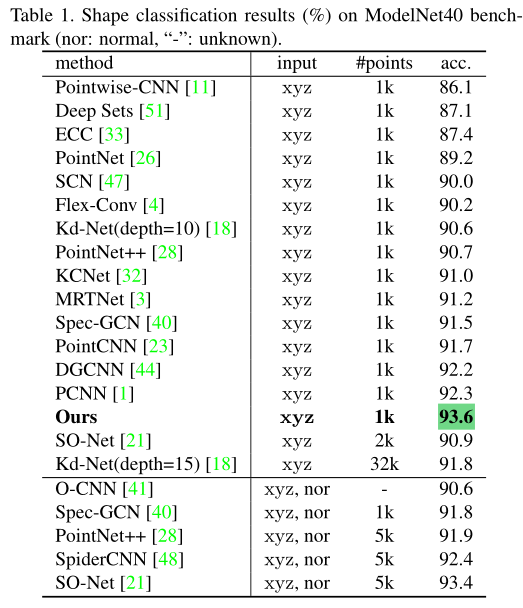
Shape classification.

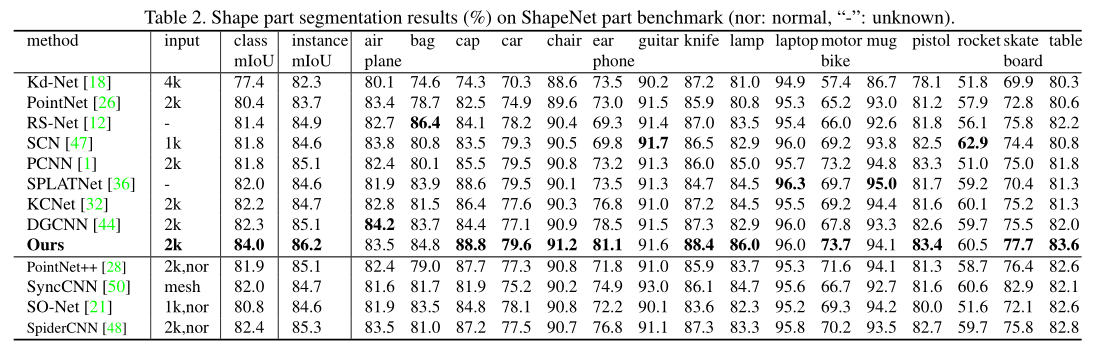
Shape part segmentation

Normal estimation

消融实验

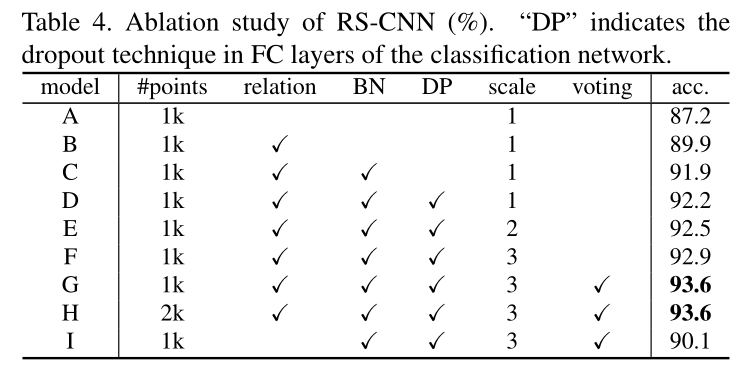
虽然在modelnet40上取得了93.6的结果，但是看消融实验可知，作者加入了很多trick才得到这样的精度，比如Pointnet++中的多尺度，以及voting test(具体是啥暂不明了)，如果去除多尺度和voting test只能达到92.2的精度。虽说创新点少，但论文中那么多的分析也需要大量的积累才能做到。

聚合函数，即\(\mathcal{A}\)的消融实验

对于low-level信息，即\(h_{ij}\)的消融实验

总结

在这项工作中，作者提出了RS-CNN，即 Relation-Shape Convolutional Neural Network，它将规则的网格CNN扩展到不规则的配置来进行点云分析。 RS-CNN的核心是一种从低维信息中学习relation的新型的卷积运算器。通过这种方式，可以对点的空间布局进行明确的推理，从而获得判断形状的意识。此外，还可以获得良好的几何关系支撑，如对刚性变换的鲁棒性。因此，RS-CNN可以实现上下文感知的形状学习，具有很高的学习效率。