快速排序算法

原理：

1. 在数列之中，选择一个元素作为"基准"（pivot），或者叫比较值。
2. 数列中所有元素都和这个基准值进行比较，如果比基准值小就移到基准值的左边，如果比基准值大就移到基准值的右边
3. 以基准值左右两边的子列作为新数列，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

 案例：

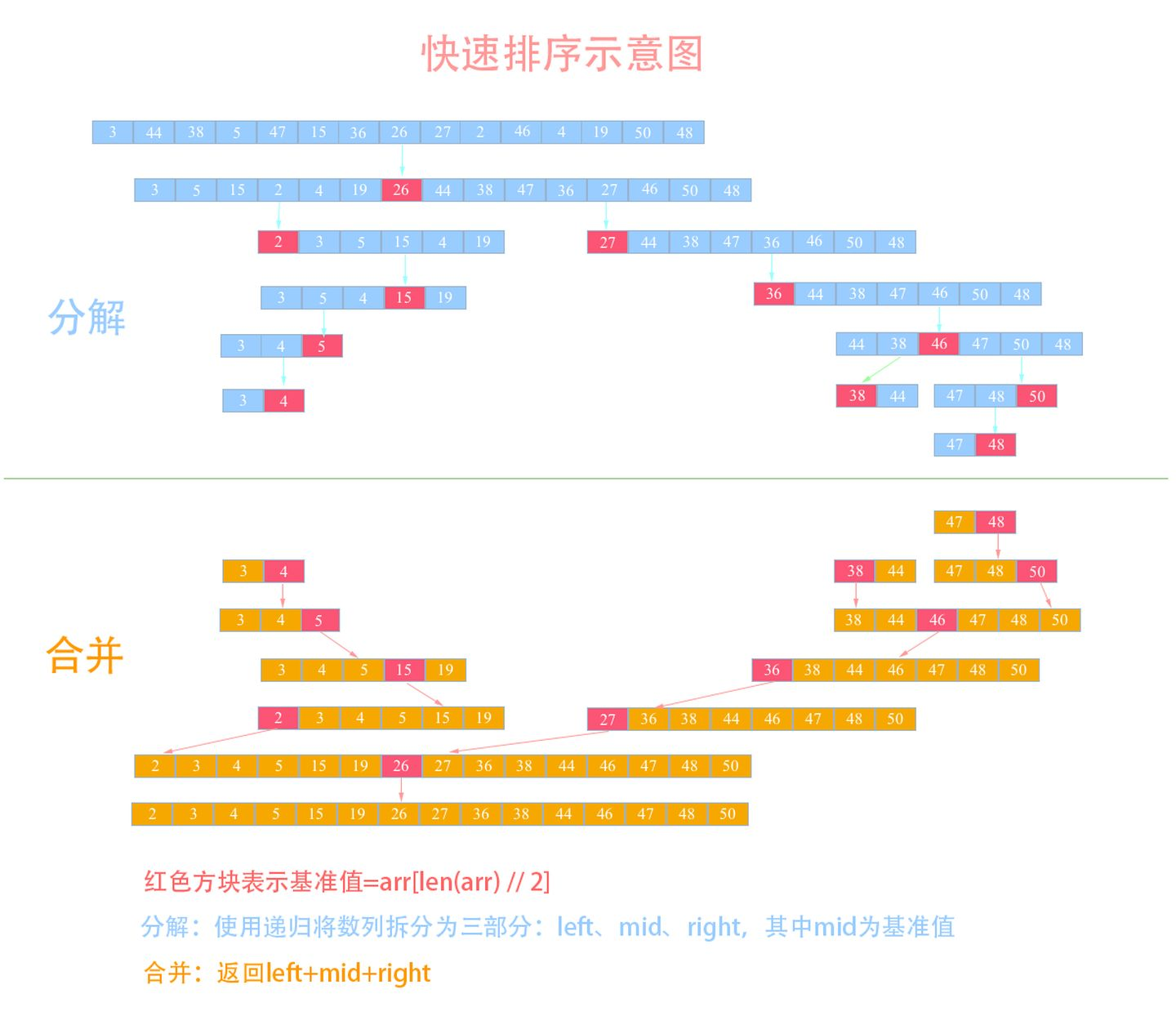
举个例子，假设我现在有一个数列需要使用快排来排序：{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48}，我们来看看使用快排的详细步骤：

1. 选取中间的26作为基准值（基准值可以随便选）
2. 数列从第一个元素3开始和基准值26进行比较，小于基准值，那么将它放入左边的分区中，第二个元素44比基准值26大，把它放入右边的分区中，依次类推就得到下图中的第二列。
3. 然后依次对左右两个分区进行再分区，得到下图中的第三列，依次往下，直到最后只有一个元素
4. 分解完成再一层一层返回，返回规则是：左边分区+基准值+右边分区

 

 代码：

def quick_sort(arr):
    """快速排序"""
    if len(arr) < 2:
        return arr
    # 选取基准，随便选哪个都可以，选中间的便于理解
    mid = arr[len(arr) // 2]
    # 定义基准值左右两个数列
    left, right = [], []
    # 从原始数组中移除基准值
    arr.remove(mid)
    for item in arr:
        # 大于基准值放右边
        if item >= mid:
            right.append(item)
        else:
            # 小于基准值放左边
            left.append(item)
    # 使用迭代进行比较
    return quick_sort(left) + [mid] + quick_sort(right)

　

算法复杂度总结：

1. 稳定性：快排是一种不稳定排序，比如基准值的前后都存在与基准值相同的元素，那么相同值就会被放在一边，这样就打乱了之前的相对顺序
2. 比较性：因为排序时元素之间需要比较，所以是比较排序
3. 时间复杂度：快排的时间复杂度为O(nlogn)
4. 空间复杂度：排序时需要另外申请空间，并且随着数列规模增大而增大，其复杂度为：O(nlogn)
5. 归并排序与快排 ：归并排序与快排两种排序思想都是分而治之，但是它们分解和合并的策略不一样：归并是从中间直接将数列分成两个，而快排是比较后将小的放左边大的放右边，所以在合并的时候归并排序还是需要将两个数列重新再次排序，而快排则是直接合并不再需要排序，所以快排比归并排序更高效一些，可以从示意图中比较二者之间的区别。