HDU 5781 ATM Mechine （概率DP）

ATM Mechine

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=5781

Description

Alice is going to take all her savings out of the ATM(Automatic Teller Machine). Alice forget how many deposit she has, and this strange ATM doesn't support query deposit. The only information Alice knows about her deposit is the upper bound is K RMB(that means Alice's deposit x is a random integer between 0 and K (inclusively)). Every time Alice can try to take some money y out of the ATM. if her deposit is not small than y, ATM will give Alice y RMB immediately. But if her deposit is small than y, Alice will receive a warning from the ATM. If Alice has been warning more then W times, she will be taken away by the police as a thief. Alice hopes to operate as few times as possible. As Alice is clever enough, she always take the best strategy. Please calculate the expectation times that Alice takes all her savings out of the ATM and goes home, and not be taken away by the police. ##Input The input contains multiple test cases. Each test case contains two numbers K and W. 1≤K,W≤2000 ##Output For each test case output the answer, rounded to 6 decimal places. ##Sample Input 1 1 4 2 20 3 ##Sample Output 1.000000 2.400000 4.523810 ##Source 2016 Multi-University Training Contest 5
##题意： Alice在ATM取钱，他不知道确切数字而只知道一个上限K，现在他要通过一系列尝试来取出所有钱，每次尝试取y，如果有y则取出，不足y则会被警告，警告超过W次会GG. Alice会尽量用少的次数去尝试，求尝试次数的期望.
##题解： 概率DP. dp[i][j]：存款上限为i，还能被警告不超过j次时的次数期望. 由于每次取的数是等概率的：每次取k∈[0,i]，其中[0,k-1]这k个数会导致这次取钱被警告. 所以不被警告的期望是 (i+1-k)/(i+1) * dp[i-k][j]; 被警告的期望是 k/(i+1) * dp[k-1][j-1]; (由于取k失败，那么剩余上限为k-1) 转移方程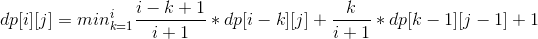：![](http://images2015.cnblogs.com/blog/764119/201608/764119-20160803171120184-793251686.png) 关键点：由于Alice会用尽量少的次数去尝试，那么他尝试的次数不会超过二分的次数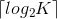：![](http://images2015.cnblogs.com/blog/764119/201608/764119-20160803171146028-149464081.png) 所以j的范围是min(15,W), 这样才能使得dp不超时.
采用记忆化搜索的形式来求DP值. 对于所有数据DP数组的值是共用的，所以只用初始化一次.(否则会TLE). 1007(HDU5787)的DP也是如此，切记.
##代码： ``` cpp #include #include #include #include #include #include #include #include #include #define LL long long #define mid(a,b) ((a+b)>>1) #define eps 1e-8 #define maxn 2100 #define mod 1000000007 #define inf 0x3f3f3f3f #define IN freopen("in.txt","r",stdin); using namespace std;

double dp[maxn][maxn];

double get_dp(int i, int j) {
if(i == 0) return dp[i][j] = 0;
if(j == 0) return dp[i][j] = inf;
if(dp[i][j] != -1.0) return dp[i][j];
double ans = inf;
for(int k=1; k<=i; k++) {
ans = min(ans, (i+1-k)/(i+1.0)get_dp(i-k,j) + k/(i+1.0)get_dp(k-1,j-1) + 1);
}
return dp[i][j] = ans;
}

int main(int argc, char const *argv[])
{
//IN;

int k,w;
for(int i=0; i<maxn; i++)
    for(int j=0; j<maxn; j++)
        dp[i][j] = -1.0;
while(scanf("%d %d", &k,&w) != EOF)
{
    printf("%.6f\n", get_dp(k,min(w,15)));
}

return 0;

}

</big>
posted @ 2016-08-03 17:13  Sunshine_tcf  阅读(240)  评论(0)  编辑  收藏  举报