【总结】线段树 进阶
↑恐怖的发表时间,你猜我第二天睡了几节课?
我竟然开了这么多坑。。。ε=(´ο`*)))唉,慢慢填吧。。。
线段树 进阶
然后我们来讲一个好玩的东西,叫权值线段树。
权值线段树&动态开点
有一个数列,数列里的每个不同的 \(a_i\) 都有一个对应的数 \(v_i\) ,表示数列中的 \(a_i\) 的个数。
所以我们的任务就是,把 \(v\) 挂到线段树上。
众所周知,线段树是可以单点修改的,为了方便,我们把单点修改 \(x\) 规定为往数列里增加一个 \(x\)。
我们让线段树中的 \([l,r]\) 区间表示 \(a_l,a_{l+1},a_{l+2},\cdots,a_r\) 每个数出现次数的和。\([x,x]\) 就表示 \(v_x\)。
注意,由于这里每一个数都有一个对应的结点,所以对于权值线段树来讲,区间不叫区间,叫值域。
咦咦咦?那干嘛要用线段树?用桶他不香嘛?
桶是挺香的,所以我们必须学线段树。 桶的区间修改和区间查询都是 \(O(n)\) 的,可以用线段树将其优化到 \(O(\log_2n)\) 。
代码呼之欲出。(就是一个简单的单点修改,区间查询,建议打一打,当复习)
Code
#include<cstdio>
#define int long long //清秀的写法
const int maxn=1e5+5;//这里 a[i] 的最大范围是 1e5
struct segment_tree{
int l,r;
int sum;//sum 表示 [l,r] 中每个数出现次数的和
}a[maxn<<2];//二倍值域
void read(int&x){
x=0;bool f=0;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch&15);ch=getchar();}
if(f)x=-x;return;
}
void build(int p,int l,int r){
a[p].l=l,a[p].r=r;
if(l==r)return;
int mid=l+r>>1;
build(p<<1,l,mid);
build((p<<1)|1,mid+1,r);
return;
}
void Update(int p,int x){
if(a[p].l==a[p].r){
a[p].sum++;//找到 x 的对应结点,将其对应个数 ++ 。
return;
}
int mid=a[p].l+a[p].r>>1;
if(x<=mid)Update(p<<1,x);
else Update((p<<1)|1,x);
a[p].sum++;//左子树和右子树中的其中之一会 ++, 会且仅会 +1, 所以干脆直接 ++ 。
return;
}
int Query(int p,int l,int r){
if(a[p].l>=l&&a[p].r<=r)
return a[p].sum;
int val=0;
int mid=a[p].l+a[p].r>>1;
if(l<=mid)
val+=Query(p<<1,l,r);
if(r>mid)
val+=Query((p<<1)|1,l,r);
return val;
}
signed main(){
//略
return 0;
}
以上是数据较小的情况。我们想,当 \(a_i\) 的范围很大,比如 \(1e8\) 的时候,我们还能这么玩吗?显然不能。于是,我们来加个名叫“动态开点”的玩意。
回顾区间修改,我们是怎么对一系列数进行修改的?
用一个懒惰标记,需要时将懒惰标记向下延伸。
那么,在不是每一个数都需要时,我们为什么要将 \(1\) ~ \(maxn\) 的每一个值域都计算一次呢?我们何不像区间修改那样,到了需要的时候再建点并计算呢?
但这样并不能实质性地优化空间,下标最大还是 \(n\times 4\) 。于是,我们考虑换一种方式求下标。
我们定义一个 \(tot\),代表下标。在插入一个 \(a_i\) 时,如果 \(a_i\) 所处于的子树是空的,也就是还没有建这个子树,我们将这个子树的下标设置为 ++tot 。
咦?那这样还怎么确定一个结点的左子树和右子树的下标?
存呀!
我们让一个结点存放:\(l,r,ll,rr,sum\) 。\(l\) 和 \(r\) 分别表示这个结点左儿子和右儿子的下标,\(ll\) 和 \(rr\) 表示当前值域的左端点和右端点,\(sum\) 表示 \([l,r]\) 中每个数出现次数的和。
那么就不能建树了,而是用更新代替建树。
询问时,判断询问的子树是否存在,如果不存在说明这个子树所代表的值域压根儿没出现过,不用查了。(这个很重要,如果不加上这个判断,就会去查询下标为 \(0\) 的结点,然后 \(0\) 结点又默认通向 \(0\) 。。。陷入死循环)
线段树的大小,就只需要 \(q*\log n\) 了。(其中 \(q\) 是添加值的次数,\(n\) 是 \(\max\{a_i\}\) )
其他和普通线段树一毛一样。
例题:小鱼比可爱(顺序对)
↑ 动态开点权值线段树模板题(不要问我为什么是道红题)
哈?你问我逆序对为毛不给 P1908?去尼玛!题解里只有一个是 正常的 动态开点权值线段树,我就说为毛一道板题我半个小时都过不了,跟题解长得一模一样都过不了!尼玛,题解也过不了!
哈?你问我为毛不给 加强版?去尼玛!离散化+普通线段树 才做得出来那玩意好嘛!正常的 动态开点权值线段树明明就做不出来!(大概?总之我在洛谷手翻几十页就没看到用权值线段树A掉的。。。
我们首先要搞清楚,题目想问什么?
比如一条鱼 \(a_i\) ,它的左边有多少条鱼没有它可爱,翻译一下,就是求 \(a_1\) ~ \(a_{i-1}\) 中比 \(a_i\) 小的值的个数。套进权值线段树里,就是 \(Query(0,a_i-1)\) 。
因为统计到 \(a_i\) 的时候,\(a_1\) ~ \(a_{i-1}\) 中每个数的个数已经被统计了,所以 \(a_1\) ~ \(a_{i-1}\) 中比 \(a_i\) 小的值(也就是 \(0\) ~ \(a_i-1\))的个数已经确定了,直接查询即可。
加上刚才的动态开点,懒得离散化。
召唤代码!
Code
#include<cstdio>
const int maxn=1e5+5;
#define int long long
struct Segment_tree{
int l,r;
int num,ll,rr;
}a[maxn];
//a开这么大是因为粘代码忘改了。。。实际上只用 100*log(INT_MAX) 就行了
//咦?不对,这两个到底哪个比较大???
int n,tot,anss,f;
inline void print(int x){
if(x<0){
putchar('-');
x=-x;
}
if(x>9)print(x/10);
putchar(x%10+'0');
return;
}
//不用建树,动态开点
void Insert(int p,int l,int r,int x){
a[p].ll=l,a[p].rr=r;//规定值域,喜欢在 Query 里重新计算值域的童鞋可以不写
if(l==r){
a[p].num++;
return;
}
int mid=l+r>>1;
if(x<=mid){
if(!a[p].l)a[p].l=++tot;//没有这棵子树,新建一个编号为 ++tot 的点
Insert(a[p].l,l,mid,x);
}
else{
if(!a[p].r)a[p].r=++tot;//同上
Insert(a[p].r,mid+1,r,x);
}
a[p].num++;
return;
}
int Query(int p,int l,int r){
if(a[p].ll>=l&&a[p].rr<=r)
return a[p].num;
int lt=a[p].l,rt=a[p].r;
int ans=0;
int mid=a[p].ll+a[p].rr>>1;
if(l<=mid&<)ans+=Query(lt,l,r);//&<:保证 lt 已经建过了
if(r>mid&&rt)ans+=Query(rt,l,r);
return ans;
}
signed main(){
scanf("%lld",&n);++tot;
for(int i=1;i<=n;++i){
scanf("%lld",&f);
printf("%lld ",Query(1,0,f-1));
Insert(1,0,2147483647,f);//题目中没有给出 a[i] 的范围,假设为 INT_MAX
}
return 0;
}
好了,经过上面的那道 入门 题,相信大家已经学会权值线段树动态开点的基本玩法了,接下来我们来康一道题~
有 shit 的 toilet
太长,请点击上方链接查看~
然后:

接着,我们来学习一种跟这个没多大关系、甚至 并不是非常重要的东西 :
线段树合并
线段树合并是个什么东西呢?字面意思,就是说把两棵线段树通过神奇的方式♂合二为一♂。
没办法,,,这破烂玩意儿只能结合着题目讲。。。
例题
Solution
思路整理:
还是先思考一个节点所储存的信息。
就先按照正常权值线段树来吧:
int num;
int l,r,ll,rr;
这道题想要我们按怎样的方法 合并(merge),更新(Insert) 与 查询(Query)?
我们先对输入的每个值进行 Insert,将每个值Insert到不同的位置。
貌似还是结合代码比较好说……?
void Insert(int&p,int l,int r,int x){
//为什么这里的p是引用变量呢?
//因为我们要把每一个人单独建一棵迷你线段树,需要用一个数组记录每一棵迷你线段树的根节点编号。
//for example:Insert(rt[1],1,inf,1)
//我们在下一行判断rt[1]是否存在,因为此时整个rt数组默认为0,每个迷你根节点都没有建。
if(!p)p=++tot;//在这里新建
a[p].num++;
//为什么这样写?
/*
当建到叶子节点时,会将这个值++
如果不是叶子节点,左子树或者右子树会++
反正都会++
干脆就在前面一起++
减少码量
*/
a[p].ll=l,a[p].rr=r;
//常规写法
if(l==r)return;
int mid=l+r>>1;
if(x<=mid)Insert(a[p].l,l,mid,x);
else Insert(a[p].r,mid+1,r,x);
return;
}
然后是查询。查询自己的子树有多少个比自己大的值。
首先我们在输入关系时存图,代码略。
然后从根节点开始,用类似于树形DP的方法递归地合并自己的子树所对应的迷你线段树。
然后 \((自己的值,inf]\) 这个比自己大的值域中所有数的个数就是当前结点的答案。
int Query(int p,int l,int r){
//十分常规
if(l<=a[p].ll&&r>=a[p].rr)
return a[p].num;
int val=0;
int lt=a[p].l,rt=a[p].r;
int mid=a[p].ll+a[p].rr>>1;
if(l<=mid&<)val+=Query(lt,l,r);
if(r>mid&&rt)val+=Query(rt,l,r);
return val;
}
void dfs(int x,int fa){
for(int i=h[x];i;i=nxt[i]){
int e=to[i];
if(e==fa)continue;
dfs(e,x);
Merge(rt[x],rt[e]);//这个等会儿再说
}
f[x]=Query(rt[x],v[x]+1,inf);//f[x]为结点x的答案
return;
}
接下来,merge应该怎么写呢?
仔细思考,比如这样两棵树 \(a\) , \(b\)
1 7
/ \ / \
2 3 8 9
/ \ \ \
4 6 10 11
(a) (b)
数字代表结点下标(即动态开点时用的 \(tot\) )
那么,合并后的树长这样:
1&7
/ \
2&8 3&9
/ \ \
4 10 6&11
(c)
其中 x&y 含义为 \(x\) 树与 \(y\) 树按题目要求合并后的结果,在本题中,x&y 就代表着 x.num+y.num
由于动态开点造成的"残疾树",对于两棵树上同一个位置上的节点 \(a_x,b_x\):
- 若 \(a_x,b_x\) 只存在其中之一 , 将 \(c_x\) 赋为存在的一项
那么这个结点的子节点和值也会同步给 \(c\) , 而不用重新计算 - 若 \(a_x,b_x\) 同时存在 , 将 \(c_x\) 看做
Update中的父结点
将\(a_x\) 和 \(b_x\) 看成子树
如:求 \(num\), 那么 \(c_x.num\) 就应该等于 \(a_x.num+b_x.num\)
继续同步递归更新 - 若 \(a_x,b_x\) 同时不存在
那还合并个毛线 , 洗洗睡吧
注 : 为了简便 , 我们把合并统一成向 \(a\) 方向合并 (也就是说将 \(c\) 替换成 \(a\))
代码很简单:
void Merge(int&x,int y){
if(!x||!y){//当 x 和 y 都为空时也会 return
x+=y;//当 y=0,x+y=x+0=x; 当 x=0,x+y=0+y=y 【妙啊】
return;
}
a[x].num+=a[y].num;
//同步修改
Merge(a[x].l,a[y].l);
Merge(a[x].r,a[y].r);
return;
}
Code
#include<cmath>
#include<cstdio>
const int inf=1e9;
const int maxn=1e5+5;
const int maxm=maxn<<1;
#define int long long
struct Segment_tree{
int l,r;
int num,ll,rr;
}a[maxn<<5];
int n,tot,cnt,x;
int v[maxn],rt[maxn],f[maxn];
int h[maxn],to[maxm],nxt[maxm];
void add(int x,int y){
to[++cnt]=y;
nxt[cnt]=h[x];
h[x]=cnt;
to[++cnt]=x;
nxt[cnt]=h[y];
h[y]=cnt;
return;
}
void read(int&x){
x=0;
bool f=0;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch&15);
ch=getchar();
}
if(f)x=-x;
return;
}
void Insert(int&p,int l,int r,int x){
if(!p)p=++tot;
a[p].num++;
a[p].ll=l,a[p].rr=r;
if(l==r)return;
int mid=l+r>>1;
if(x<=mid)Insert(a[p].l,l,mid,x);
else Insert(a[p].r,mid+1,r,x);
return;
}
void Merge(int&x,int y){
if(!x||!y){
x+=y;
return;
}
a[x].num+=a[y].num;
Merge(a[x].l,a[y].l);
Merge(a[x].r,a[y].r);
return;
}
int Query(int p,int l,int r){
if(l<=a[p].ll&&r>=a[p].rr)
return a[p].num;
int val=0;
int lt=a[p].l,rt=a[p].r;
int mid=a[p].ll+a[p].rr>>1;
if(l<=mid&<)val+=Query(lt,l,r);
if(r>mid&&rt)val+=Query(rt,l,r);
return val;
}
void dfs(int x,int fa){
for(int i=h[x];i;i=nxt[i]){
int e=to[i];
if(e==fa)continue;
dfs(e,x);
Merge(rt[x],rt[e]);
}
f[x]=Query(rt[x],v[x]+1,inf);
//比 v[x] 大的值域 : (v[x],inf]
return;
}
signed main(){
read(n);
++tot;
for(int i=1;i<=n;++i){
read(v[i]);
Insert(rt[i],1,inf,v[i]);
}
for(int i=2;i<=n;++i){
read(x);
add(i,x);
}
dfs(1,-1);
for(int i=1;i<=n;++i)
printf("%lld\n",f[i]);
return 0;
}

最后的最后,
扫描线
还是结合例题。
亚特兰蒂斯问题
双倍快乐
Solution
我们针对更难的、需要多组输入和存储浮点数的第一题来讲。
总的来说,就是输入矩形,求他们的面积之和,如果一块面积被多次覆盖,只算 \(1\) 次。
那么,这玩意咋搞?
当然是容斥原理瞎搞
咳咳,怎么可能~
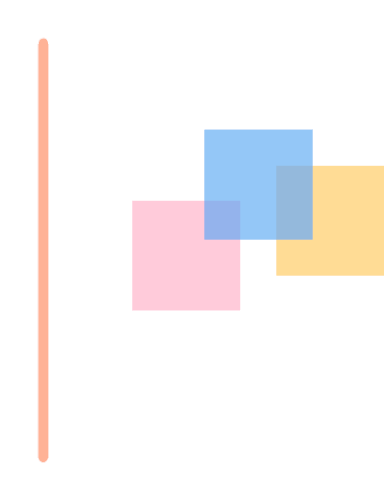
如图所示。这里有三个矩形和一根线。(姑且称之为扫描线)
我们用这根线来扫一扫扫描遍历这三个矩形的高,也就是说,对每一条竖着的线段进行扫描,遇到一根竖着的线段就停下来。
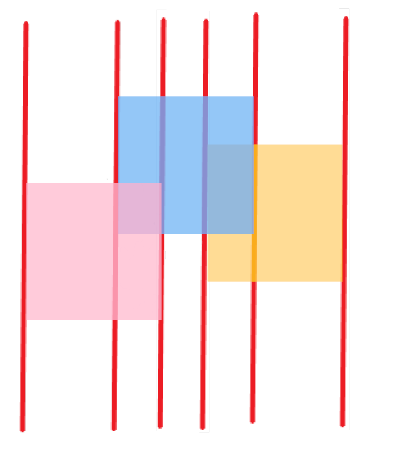
红线处就是扫描线停下来的地方。
那么,我们要把标红线处切开!

我们发现,现在它们就由一个不规则图形变成了一个个珂以通过底和高求出面积的矩形。
但是,我们不知道它们的高啊!
接下来,我们来做一个神奇的操作:
如果红线处是一个矩形的左边的边,我们就将这条边(起点:\((x,y_1)\),终点:\((x,y_2)\))对应的 \((y_1,y_2)\) 这整条线段 \(+1\),否则就 \(-1\),再把当前红线上做完以上操作后值不为 \(0\) 的线段标成绿色,看看会发生什么!
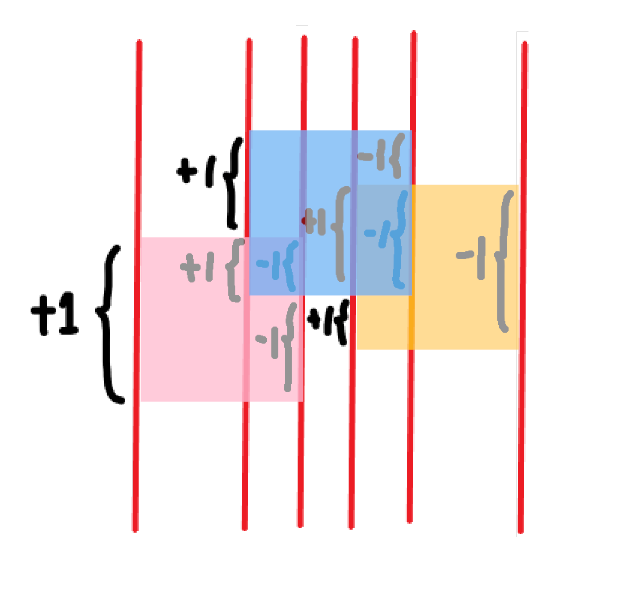
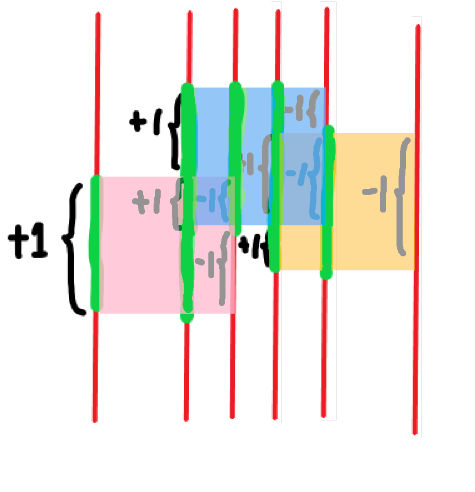
这,这不是切开后每一个小矩形的高嘛!
我都暗示得这么明显了。。。所以,用线段树记录每条线段的值,最后再在每一根红线的地方 Update 当前红线的信息就行了。
具体实现
离散化和存线段不想讲。(已经快1点了好伐!今天7点又要起来。。。)
每一个结点,定义一个 \(len\) 与 \(cnt\),\(cnt\) 表示当前线段的值,\(len\) 表示当前线段可求高的总长度(也就是不为 \(0\) 的线段总长)
因为我不想用结构体,所以我们在函数内传区间左右端点,用两个数组保存 \(len\) 和 \(cnt\)。
void Update(int p,int l,int r,int ql,int qr,int f){
int mid=l+r>>1;
int lt=p<<1;int rt=lt|1;
if(ql<=l&&r<=qr){
acnt[p]+=f;
if(acnt[p])alen[p]=Lsh[r]-Lsh[l];
//Lsh[x]是指离散化后的x原本的值。
//如果当前线段一整段都有值,当前线段的一整段都可以算上。
else alen[p]=alen[lt]+alen[rt];
//否则就是说明在某个儿子中断开了,直接将儿子所对应的值相加即可。
return;
}
if(l+1==r)return;
if(ql<=mid)Update(lt,l,mid,ql,qr,f);
if(qr>mid)Update(rt,mid,r,ql,qr,f);
if(acnt[p])alen[p]=Lsh[r]-Lsh[l];
else alen[p]=alen[lt]+alen[rt];
//同上
return;
}
其实难点在于对于 pushup(if(acnt[p])...) 的理解和离散化。
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
#define db double
const int maxn=1e5+5;
struct __ly_nb__{
db x,y1,y2;
int f;
__ly_nb__(db X=0,db Y1=0,db Y2=0,int F=0){
x=X,y1=Y1,y2=Y2,f=F;
}
bool operator<(const __ly_nb__ q)const{
return x<q.x;
}
}zszz[maxn];
db Lsh[maxn];
db alen[maxn<<2];
int acnt[maxn<<2];
db x1,y1,x2,y2,ans;
int n,cnt,upy,dny,id;
void init(void){//记得初始化
memset(Lsh,0,sizeof(Lsh));
memset(alen,0,sizeof(alen));
memset(acnt,0,sizeof(acnt));
x1=y1=x2=y2=ans=0.0;
cnt=upy=dny=0;
}
void Update(int p,int l,int r,int ql,int qr,int f){
int mid=l+r>>1;
int lt=p<<1;int rt=lt|1;
if(ql<=l&&r<=qr){
acnt[p]+=f;
if(acnt[p])alen[p]=Lsh[r]-Lsh[l];
else alen[p]=alen[lt]+alen[rt];
return;
}
if(l+1==r)return;
if(ql<=mid)Update(lt,l,mid,ql,qr,f);
if(qr>mid)Update(rt,mid,r,ql,qr,f);
if(acnt[p])alen[p]=Lsh[r]-Lsh[l];
else alen[p]=alen[lt]+alen[rt];
return;
}
signed main(){
while((~scanf("%lld",&n))&&n){
init();
for(int i=1;i<=n;++i){
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
zszz[++cnt]=__ly_nb__(x1,y1,y2,1);
Lsh[cnt]=y1;
zszz[++cnt]=__ly_nb__(x2,y1,y2,-1);
Lsh[cnt]=y2;
}
//正常离散化
sort(zszz+1,zszz+cnt+1);//STL大法好
sort(Lsh+1,Lsh+cnt+1);//STL大法好
int cnt1=unique(Lsh+1,Lsh+cnt+1)-Lsh-1;//STL大法好
for(int i=1;i<=cnt;++i){
ans+=alen[1]*(zszz[i].x-zszz[i-1].x);
upy=lower_bound(Lsh+1,Lsh+cnt1+1,zszz[i].y1)-Lsh;//STL大法好
dny=lower_bound(Lsh+1,Lsh+cnt1+1,zszz[i].y2)-Lsh;//STL大法好
Update(1,1,cnt1,upy,dny,zszz[i].f);
}
printf("Test case #%d\n",++id);
printf("Total explored area: %.2lf\n",ans);
}
return 0;
}
对不起我写不下去了。。。为什么我总是只有在 \(23\) 点~ \(1\) 点才有空写博客啊啊啊啊!
谢谢读者大人们,现在一定正有一个即将 \(\texttt{AK IOI}\) 的帅气的小哥哥/可爱的小姐姐正在看这段字,并且点了个赞。
不要脸地求赞赞
end.
—— · EOF · ——
真的什么也不剩啦 😖


