吴恩达机器学习课后作业--ex1

单变量的线性回归

问题：在ex1data1.txt中有两列数据，第一列是城市人口数量，第二列是该城市小吃店利润，目的是根据城市人口数量来预测小吃店的利润

需要用到的公式

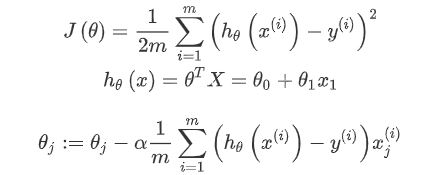
实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

numpy用来进行矩阵的运算，pandas常用来进行数据的操作，matplotlib主要用来可视化

读取数据集

path= "D:\\ML\\ML\\Linear Regression with One Variable\\ex1data1.txt"
data = pd.read_csv(path,header=None,names=['Population','Profit'])#文件读取
data.head()#显示数据
data.plot(kind='scatter',x='Population',y='Profit',figsize=(12,8))
plt.show()

计算损失函数J(Ѳ)

def computeCost(X,y,theta):
    inner = np.power(((X*theta.T)-y),2)
    return np.sum(inner)/(2*len(X))

对数据集进行处理

data.insert(0,'Ones',1)#在第0列插入1，列名为Ones
#初始化变量X和y
#data.shape输出(行数，列数)，所以shape[1]就为列数
cols = data.shape[1]#计算列数
#[起始行:终止行,起始列：终止列]
X = data.iloc[:,:-1]#除最后一列  iloc是前闭后开，从0开始，提取指定行和列
y = data.iloc[:,cols-1:cols]#最后一列

X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))#array转matrix,具体看array和matrix的区别

梯度下降算法

def gradientDescent(X,y,theta,alpha,iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])#ravel扁平化操作变成一维,计算参数的个数
    cost = np.zeros(iters)
    for i in range(iters):
        error = (X*theta.T)-y
        for j in range(parameters):
            term = np.multiply(error,X[:,j])
            temp[0,j] = theta[0,j]-((alpha/len(X))*np.sum(term))
        theta = temp
        cost[i] = computeCost(X,y,theta)
    return theta,cost

设置学习率和迭代次数并执行

alpha = 0.01
iters = 1500
g,cost = gradientDescent(X,y,theta,alpha,iters)

可视化

#可视化
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x)
fig, ax = plt.subplots(figsize=(12,8))#拟合曲线
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
plt.plot(range(0,1500),cost)
plt.show()

pandas:

pd.read_csv(filename)：从CSV文件导入数据

data.head(n)默认显示数据的前5行

data.plot(kind='scatter',x='Population',y='Profit',figsize=(12,8))画图

data.shape() 获取data的行数和列数，是一个元组

data.shape[1] 得到data的列数

data.iloc[:,:-1]  获取data的部分数据，里面的含义是[起始行:终止行,起始列：终止列]，包含的数据是前闭后开

data.insert(0,'Ones',1) 在第0列插入，值为1 

numpy:

np.power(data,2) 对矩阵中的元素求平方

np.sum(data)对矩阵中的元素求和

np.matrix(X.values)转化为矩阵

data.ravel()对数据进行扁平化

np.multiply对应位置相乘，*是矩阵乘法

x = np.linspace(data.Population.min(), data.Population.max(), 100)生成元素个数为100的等间隔数列。而前两个参数分别是数列的开头与结尾。