DP动态规划

动态规划和分治没有根本上的区别（关键看有无最优子结构）

共性：找到重复子结构

差异性：最优子结构，中途可以淘汰次优解

问题一：斐波那契数列

int fib(int n)
{
   if(n<=1) return n;
   else 
      return fib(n-1)+fib(n-2);
}

可以利用记忆数组进行优化

int fib(int n,int memo[])
{
   if(n<=1) return n;
   else if(memo[n]==0)
       return fib(n-1)+fib(n-2);
   return memo[n];
}

这样就把指数级的时间复杂度降到了O(n)

问题2 count the paths

计算从start到end共有多少条路径

方法一：自顶向下

采用分治的思想

path[start] = path[A]+paths[B]

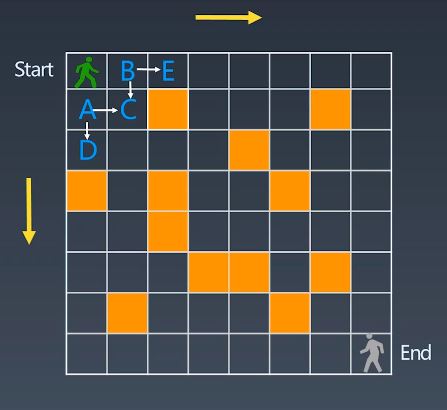
int countPaths(bool[][] grid,int row,int col)
{
    if(!isWall())  return 0;
    if(isEnd())  return 1;
    return countPaths(grid,row+1,col)+countPaths(grid,row,col+1);    
}

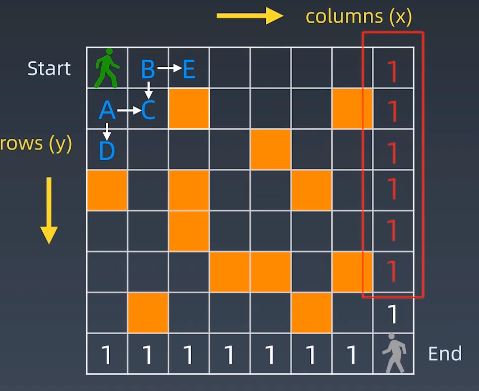
方法二 自底向上

只能向下或向右，那么到达最下方和最右方时只有1种走法。那么paths[i][j]=paths[i+1][j]+paths[i][j+1],以此类推可以得到开始先走A和开始先走B分别是10种和17种，所以一共有27种。

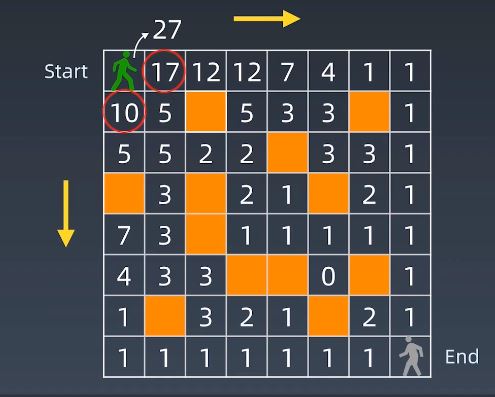
int countPaths(int m,int n)
{
   int grid[m][n];
   for(int i=0;i<n;i++) grid[i][0]=1;
   for(int j=0;j<;j++) grid[0][j]=1;
   for(int i=1;i<m;i++){
     for(int j=1;j<n;j++)
        grid[i][j]=grid[i-1][j]+grid[i][j-1];
   }
    return grid[m-1][n-1];
}