数据结构
数据结构
哈希表、树状数组、线段树......
由于这些知识点较为基础,相信各位神仙都会,因此不再赘述(斜眼笑)
可持久化数据结抅之主席树
就是可持久化权值线段树
利用前缀和思想,每个位置的那棵树比前一个位置的那棵树多一个值
那么每次查询在两棵线段树上二分即可
void add(int &p,int q,int l,int r,int x)
{
p = ++ cnt; tr[p] = tr[q]; tr[p].siz ++;
if(l == r) return;/**/
int mid = (l + r) >> 1;
if(x <= mid) add(tr[p].ls,tr[q].ls,l,mid,x);
else add(tr[p].rs,tr[q].rs,mid + 1,r,x);
}
int ask(int p,int q,int l,int r,int x)
{
if(l == r) return b[l];
int mid = (l + r) >> 1;
int L = tr[tr[q].ls].siz - tr[tr[p].ls].siz;
if(L >= x) return ask(tr[p].ls,tr[q].ls,l,mid,x);
else return ask(tr[p].rs,tr[q].rs,mid + 1,r,x - L);
}
int main()
{
n = read();m = read();
for(int i = 1;i <= n;i ++){a[i] = read();b[i] = a[i];}
sort(b + 1,b + n + 1);
for(int i = 1;i <= n;i ++)
{
int d = lower_bound(b + 1,b + n + 1,a[i]) - b;
add(rt[i],rt[i - 1],1,n,d);
}
for(int i = 1,k,l,r;i <= m;i ++)
{
l = read();r = read();k = read();
printf("%d\n",ask(rt[l - 1],rt[r],1,n,k));
}
}
例题
这道题怎么做呢?你把主席树给它推广一下不就行了嘛。
我们以前求一段区间是右端点减去左端点。
现在放到树上怎么办呢?
树上差分呗。
又考虑到点权,所以将u和v的主席树加起来再减去\(lca\)和\(fa[lca]\)的主席树。
在考虑往左边走还是往右边走。
2.P3066 [USACO12DEC]逃跑的BarnRunning Away From…
既然是讲主席树,我们显然也可以用主席树来维护,只要在\(dfn\)序上建主席树就行了。
那么\(dfn\)序在\(dfn[x]\)到\(dfn[x]+size[x]-1\)范围内的即为\(x\)的子树。
其实这道题还有一个方法,倍增加树上差分即可,有兴趣的同学自己尝试哈
我们先建立一下主席树,然后我们怎么找到这个数是谁呢?
考虑,这个数如果大于一半,那么他所在的那个区间也是一定大于一半的。
那么每次在主席树上二分查找即可。
这道题显然是区间修改,单点查询。
貌似很熟悉,像极了树状数组......
因此考虑差分,在\(s\)处加,在\(e + 1\)处减去即可。
除此之外,用主席树对\(n\)棵权值线段树做前缀和即可。
左偏树
为什么它叫做左偏树呢?
因为它的左子树比右子树节点多,也就是它左偏。
咳咳,进入正题——
我们引入一个概念:外结点。
一颗左偏树中的外结点为左子树或右子树为空的节点。
此外,我们定义一个节点\(i\)的距离为\(dis[i]\),表示从\(i\)到它的子树内最近的外结点经过的边数。
由于左偏树左偏,因此可得:任意节点的左子节点的距离不小于右子节点的距离。
详见图片:
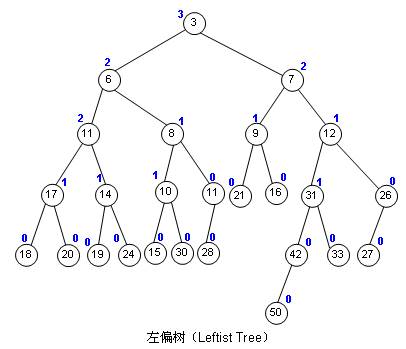
那么怎么合并呢,详再见图片:
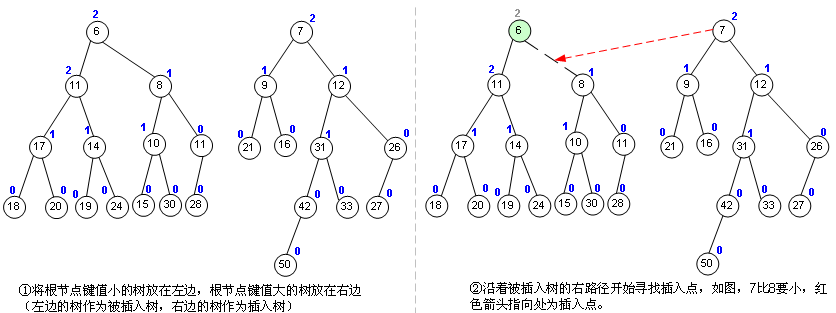
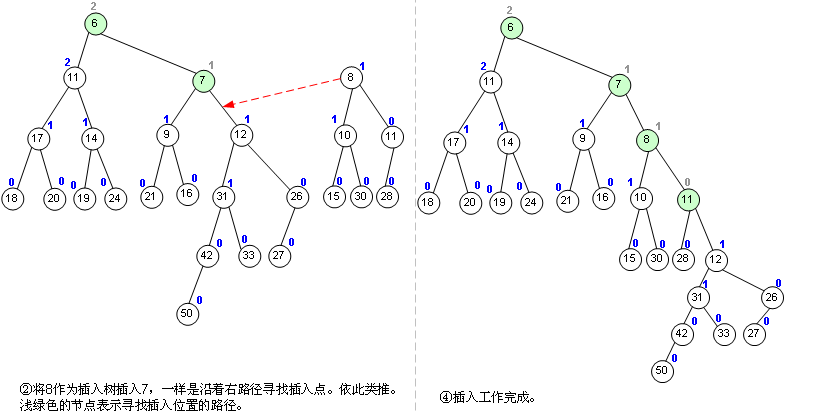
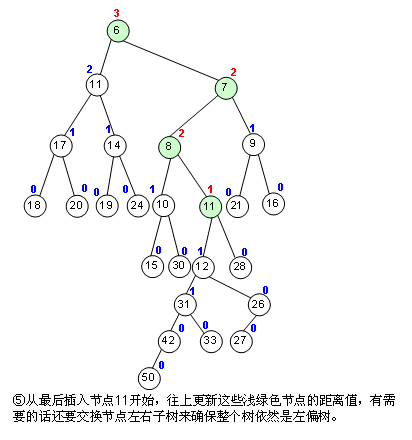
根据左偏性质,我们还可以得到左偏树定理:若一棵左偏树有\(n\)个节点,则该左偏树的距离不超过\(log_2(n + 1) - 1\),\(why\)?
当一棵左偏树的距离\(k\)一定时,当且仅当该左偏树是完全二叉树时,节点数目最少(证明显然)。
好吧还是证明一下:
当一棵树是完全二叉树时,我们随便去掉一个叶子结点,它的距离都会变小。
而在下面增加节点时,它的距离不变。
因此它的结点总数\(n\)至少是\(2 ^ {(k + 1)} - 1\),即\(n \ge 2 ^ {(k + 1)} - 1\)
所以\(k \le log_2(n + 1) - 1\)
这样我们就可以保证它合并的时间复杂度为\(O(log \space n)\)
int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}
int merge(int x,int y)
{
if(!x || !y) return x + y;
if(val[x] > val[y] || (val[x] == val[y] && x > y)) swap(x,y);
rs[x] = merge(rs[x],y);
fa[ls[x]] = fa[rs[x]] = fa[x] = x;
if(dis[ls[x]] < dis[rs[x]]) swap(ls[x],rs[x]);
dis[x] = dis[rs[x]] + 1;
return x;
}
void Union(int x,int y)
{
int xx = find(x),yy = find(y);
if(vis[x] || vis[y] || xx == yy) return;
fa[xx] = fa[yy] = merge(xx,yy);
}
void Delete(int x)
{
vis[x] = 1;
fa[ls[x]] = ls[x]; fa[rs[x]] = rs[x];
fa[x] = merge(ls[x],rs[x]);
}
int get_ans(int x)
{
if(vis[x]) return -1;
int xx = find(x);
Delete(xx);
return val[xx];
}
void work()
{
n = read();m = read();
for(int i = 1;i <= n;i ++) val[i] = read();
for(int i = 1;i <= n;i ++) fa[i] = i;
for(int i = 1,opt,x,y;i <= m;i ++)
{
opt = read();x = read();
if(opt == 1) {y = read(); Union(x,y);}
else printf("%d\n",get_ans(x));
}
}
int main() {return work(),0;}
例题
跟模板题一毛一样滴。。。
其实跟模板题也是一毛一样滴,拿出来一个数减半,然后放回去合并。。。
首先显然的是我们要从叶子结点\(dfs\)向上推,维护目前存活的骑士。
由于攻击力\(\leq h[i]\)的骑士会在该节点\(i\)死亡, 因此我们维护一个最小堆。
初始时将到达此节点的所有骑士放进去,每次一直\(pop\),更新在此死去的骑士\(and\)该骑士攻占的城池数量,直至堆顶骑士攻击力\(\geq h[i]\)。
那么考虑如何更新骑士的攻击力呢?(总不能\(O(n)\)扫一遍堆)
我们在根节点打上乘法\(tag \space and\)加法\(tag\)不就好了么...
首先我们对每个节点维护一个大根堆,\(why?\)
因为当费用超过总预算时,贪心思想,我们显然要将费用最高的忍者依次弹出,直至总费用不超过总预算(保证领导力相同时,忍者个数最多)
同时维护堆内忍者个数和费用和
接着我们\(dfs\)从下往上合并即可
别忘了\(long \space long\)
此外扔几个练习题:
1.P4331 [BalticOI 2004]Sequence 数字序列
平衡树
据某宋同学说,你们平衡树掌握的挺好的,因此我就不多讲了,基础你们来,习题我们一起上,冲鸭——
Splay
时间复杂度均摊\(O(n logn)\)(证明别问,问就是不会)
首先来一波旋转
rotate
(以右旋为例)
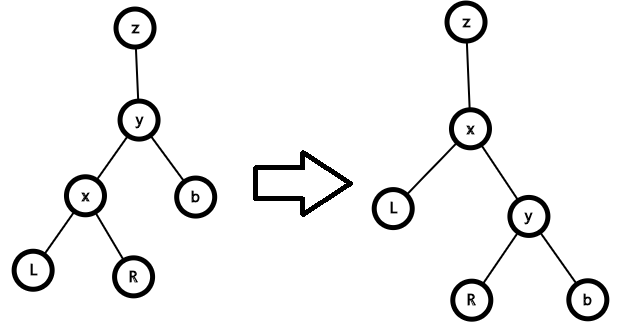
我们要将\(x\)转上去,那么为了维护\(BST\)的性质,\(y\)需要成为\(x\)的右儿子,那么原来\(x\)的右儿子怎么办呢?
此时\(y\)的左儿子其实已经空了,因此我们可以将原来\(x\)的右儿子放到\(y\)的左儿子上。
而且此时仍然满足\(BST\)性质。
左旋同理。
splay
伸展操作,我们需要将\(x\)这个节点转到指定节点(一般是根)
那么我们直接将它\(rotate\)到根吗?
答案当然是否定的(如果一直旋转的话,那么考虑一条链时它将一直都是一条链,可以自己手画尝试一下)
于是为了应付这种情况,我们采用双旋方式,先转它的父亲,再转它。
这样树的期望高度是\(log \space n\)的(具体证明,还是不会)
这样,基本操作就完了。
此外,普通平衡树的6种操作:插入,删除,求排名,求第k大,求前驱,求后继。
在每次操作之后都要把对应的节点转到根。
对此,百度百科是这样解释的。
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。splay tree应运而生。splay tree是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
一些人说这跟\(Splay\)的均摊时间复杂度有关,每次把节点转到根可以摊还一定的时间复杂度。记住就好
insert
如果插入时,书中没有任何节点,那么他就是根节点
否则不断跳节点将该点插入对应的位置即可
delete
参考\(Treap\)我们用一个简便的方法
将该节点转到根节点处,然后合并左右子树即可
rank
直接向下找即可,别忘了\(rank\)是关键词,考试千万别用
kth
和求排名差不多,不多说
pre
\(x\)对应的排名减一即为它的前驱
next
求后继,\(x + 1\)的排名对应的数就是它的后继
\(next\)也是关键词,千万别用
下面贴个代码(忘了的同学可以适当借鉴)
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 100005;
int n,root,sta[N * 30],tail,cnt,v[N * 30],tr[N * 30][2],fa[N * 30],size[N * 30];
inline int read()
{
int x = 0,f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}
return x * f;
}
void up(int x) {size[x] = size[tr[x][0]] + size[tr[x][1]] + 1;}//+1
bool isr(int x) {return tr[fa[x]][1] == x;}
int em(int x) {return size[tr[x][0]] + 1;}
void rot(int x)
{
int k = isr(x),y = fa[x],z = fa[y],w = tr[x][!k];
if(y == root) root = x;
else tr[z][isr(y)] = x;
fa[x] = z; fa[y] = x; tr[x][!k] = y; tr[y][k] = w;
if(w) fa[w] = y;//
up(y); up(x);
}
void splay(int x)
{
while(x != root)
{
if(fa[x] != root) rot((isr(x) == isr(fa[x])) ? fa[x] : x);
rot(x);
}
}
void Insert(int val)
{
if(!root)
{
root = tail ? sta[tail --] : ++ cnt;
v[root] = val; size[root] = 1;//size
return;
}
int x = root,last = 0;
while(x)
{
last = x;//
x = tr[x][val > v[x]];
}
x = tail ? sta[tail --] : ++ cnt;
tr[last][val > v[last]] = x; fa[x] = last;
v[x] = val; size[x] = 1;//size
splay(x);
}
int merge(int x,int y,int f)
{
if(x) fa[x] = f;
if(y) fa[y] = f;
if(!x || !y) return x + y;
tr[x][1] = merge(tr[x][1],y,x);
up(x); return x;
}
void Delete(int val)
{
int x = root;
while(x && v[x] != val) x = tr[x][val > v[x]];
if(!x) return;
splay(x); root = merge(tr[x][0],tr[x][1],0);
sta[++ tail] = x;
tr[x][0] = tr[x][1] = size[x] = fa[x] = v[x] = 0;
}
int rnk(int val)
{
int res = 0;
int x = root,last = root;
while(x)
{
last = x;
if(v[x] >= val) x = tr[x][0];
else res += em(x),x = tr[x][1];
}
splay(last); return res + 1;
}
int kth(int k)
{
int x = root;
while(x && em(x) != k)
{
if(em(x) > k) x = tr[x][0];
else k -= em(x),x = tr[x][1];
}
splay(x); return v[x];
}
int pre(int val)
{
int x = root,last = root;
while(x)
{
if(v[x] < val) last = x,x = tr[x][1];//
else x = tr[x][0];
}
return splay(last),v[last];
}
int nex(int val)
{
int x = root,last = root;
while(x)
{
if(v[x] > val) last = x,x = tr[x][0];
else x = tr[x][1];
}
return splay(last),v[last];
}
void work()
{
n = read();
for(int i = 1,opt,x;i <= n;i ++)
{
opt = read();x = read();
if(opt == 1) Insert(x);
if(opt == 2) Delete(x);
if(opt == 3) printf("%d\n",rnk(x));
if(opt == 4) printf("%d\n",kth(x));
if(opt == 5) printf("%d\n",pre(x));
if(opt == 6) printf("%d\n",nex(x));
}
}
int main() {return work(),0;}
例题
在此只讲述\(Splay\)做法(主要是我只用\(Splay\)写了这个题)
之前的\(Splay\)我们维护的是权值,现在我们要维护一下位置。
考虑区间翻转怎么办呢?借鉴一下线段树的思想:打标记。
那么这一段区间在树上可能不连续怎么办呢?
我们可以将区间旋转出来:对于一段区间\([l,r]\),我们将\(l-1\)转到根,将\(r +1\)转到根的右儿子,那么根的右儿子的左节点即为这段区间。
然后我们给该节点打上标记,代表将区间翻转了,之后用到的时候再翻转即可。
为了保证翻转$1 \(~\) n$这段区间的时候不出锅,我们插入一个极大值,一个极小值即可。
FHQ Treap
\(FHQ \space Treap\)是什么呢?它也叫无旋\(Treap\),是\(Treap\)的加强版,它不依靠旋转来平衡,但是常数也是较大的...(总比BST强)
但是不依靠旋转来平衡我们怎么办呢?
我们用\(rand\)——随机数据下,树的期望高度是\(logn\)的,那么我们构造的树就会很平衡。
也就是说,我们队每个节点维护一个键值,而这个键值就是\(rand\)得来的,我们依靠它来平衡。
同时我们也要保证整棵树的键值是个小根堆。
split
分裂操作,将一棵\(Treap\)分裂为两棵\(Treap\)
我们将以\(x\)为根的子树递归下去,分为\(l\)和\(r\)两部分(依据权值划分)
如果\(x\)的左子树的权值比\(val\)小,我们可以直接\(x\)的左子树给\(l\),然后递归建立右子树
否则将\(x\)的右子树给\(r\),然后递归建立左子树
最后别忘了\(up\)
merge
合并操作,将两棵子树合并到一起
别忘了保证左子树的权值都小于右子树的
因此我们按照键值维护小根堆来合并
若\(l\)的键值小,就将\(l\)的左子树给\(x\),递归建右子树
否则将\(r\)的右子树给\(x\),递归建左子树
kth
就是看这个点在子树内的排名是不是等于\(k\)
若大于\(k\)去左边找;反之将左边的贡献减掉,去右边找
insert
特判没有节点的情况,直接将\(root\)赋过去
然后按照\(val\)进行\(split\),最后将三棵子树按照上述规则两两合并
delete
通过\(split\)将权值为\(val\)的点分裂出来
然后只删除一个,将左右子树合并
rank
将小于\(val\)的子树\(split\)出来,看看该子树里面有多少节点,加一即为排名
kth
和上面一样直接求即可
pre
将小于\(val\)的子树分离出来
然后找子树中最大的那个,最后别忘了合并
next
将大于\(val\)的子树分离出来
然后找子树中最小的那个,最后别忘了合并
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
const int N = 100005;
int n, cnt, root;
struct node
{
int ch[2], siz, val , key;
inline void init() {ch[0] = ch[1] = val = 0; siz = 1; key = rand();}
}tr[N * 30];
inline int read()
{
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-')f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar(); }
return x * f;
}
void up(int x) {tr[x].siz = tr[tr[x].ch[0]].siz + tr[tr[x].ch[1]].siz + 1; }
int em(int x) {return tr[tr[x].ch[0]].siz + 1; }
void split(int o, int &l, int &r, int val)
{
if(!o) {l = r = 0; return; }
if(tr[o].val <= val) return l = o, split(tr[o].ch[1], tr[l].ch[1], r, val), up(l);
else return r = o, split(tr[o].ch[0], l, tr[r].ch[0], val), up(r);
}
void merge(int &o,int l,int r)
{
if(!l || !r) {o = l + r; return; }
if(tr[l].key <= tr[r].key) return o = l, merge(tr[o].ch[1], tr[l].ch[1], r), up(o);
else return o = r, merge(tr[o].ch[0], l, tr[r].ch[0]), up(o);
}
void Insert(int val)
{
if(!root) {root = ++ cnt; tr[root].init(); tr[root].val = val; return; }
int x = 0, y = 0, z = ++ cnt; tr[z].init(); tr[z].val = val;
split(root, x, y, val);
merge(x, x, z);
merge(root, x, y);
}
void Delete(int val)
{
int x = 0, y = 0, z = 0;
split(root, x, y, val);
split(x, x, z, val - 1);
merge(z, tr[z].ch[0], tr[z].ch[1]);
merge(x, x, z);
merge(root, x, y);
}
int rnk(int val)
{
int x = 0, y = 0;
split(root, x, y, val - 1);
int res = tr[x].siz + 1;
merge(root, x, y);
return res;
}
int kth(int x, int k)
{
int now = x;
while(em(now) != k)
{
if(em(now) > k) now = tr[now].ch[0];
else k -= em(now), now = tr[now].ch[1];
}
return now;
}
int kth(int k)
{
return tr[kth(root,k)].val;
}
int pre(int val)
{
int x = 0, y = 0;
split(root, x, y, val - 1);
int res = tr[kth(x, tr[x].siz)].val;
merge(root, x, y);
return res;
}
int nex(int val)
{
int x = 0, y = 0;
split(root, x, y, val);
int res = tr[kth(y, 1)].val;
merge(root, x, y);
return res;
}
void work()
{
n = read();
for(int i = 1, opt, x; i <= n; i ++)
{
opt = read(); x = read();
if(opt == 1) Insert(x);
if(opt == 2) Delete(x);
if(opt == 3) printf("%d\n",rnk(x));
if(opt == 4) printf("%d\n",kth(x));
if(opt == 5) printf("%d\n",pre(x));
if(opt == 6) printf("%d\n",nex(x));
}
}
int main() {return work(), 0; }
替罪羊树
替罪羊树是一种优雅的数据结构,想问\(why?\)
暴力即优雅...
而替罪羊树完美体现了这一点
\(Sunny\)_\(r\):当你的树不平衡了怎么
办?
\(splay\):我旋转
\(FHQ \space Treap\):我\(rand\)
替罪羊树:都让让,老子拍扁重建
\(splay \space and \space FHQ \space Treap\):...
红黑树
有兴趣的同学,请自学...(主要是我不会)
例题
我们考虑这一天的值是固定的,那么我们显然就是要去找一个最接近这个值的数。
那么我们考虑两种情况。
- 要找的数比这个值大,我们要求这个数尽可能地小
- 要找的数比这个值小,我们要求这个数尽可能地大
等等。。。这不就一个前驱,一个后继嘛。
套上平衡树,没了。
这个题有一个很好的性质。就是顾客和宠物不会同时存在,那就比较省事了,不然还需要维护两颗\(Splay\)。。。然后又是一堆东西。
考虑这道题怎么做,有了上一道题的经验。可以很快发现其实也就是前驱和后继。然后就是再加个插入和删除就行了。
只需要知道当前是顾客多还是宠物多
然后相应的建出宠物树或者顾客树,相应查询即可
整体加
难道我们需要一个一个加?那不\(TLE\)成\(dog\)了嘛...
其实吧,基本上所有整体加的题目,我们都是只需要维护一个整体标记就行了。
那么这道题显然也可以。
那么一个员工的实际工资,加加减减搞一搞就行了。
还有一个问题就是,新来的员工,人家并没有经历过工资的变化,其实就是标记对他是不对的。
那怎么办呢?我们得想办法让他也适用啊。(不然,你还能再维护标记?)
那你直接先给他减去加标记即可。
其实这种题就是平衡树的另一种用途的应用。就是用平衡树维护序列,而这种情况维护用Splay。
那么我们来考虑考虑怎么维护。
- 操作1,我们需要把x放到最高的地方,也就是让它在平衡树上处在最左节点,然后我们可以把它直接转到根,把左子树放到x的后继的左子树就行了。
- 操作2,我们需要把x放到最低的地方,也就是让它在平衡树上处在最右节点,然后我们也是把它转到根,把右子树放到x的前驱的右子树就行了。
- 操作3,-1的话,就是让我们和它的前驱换一下地,我们可以求出前驱,然后把两个节点的信息交换就行了,0的话,不用动,1的话,就是和后继交换信息。
- 操作4,其实就是求它的排名就行了。
- 操作5,其实就是第k大。
一些习题自己写吧:
4.SP1043 GSS1 - Can you answer these queries I
树套树
线段树套线段树
平衡树套线段树
树状数组套主席树
线段树套平衡树...
树状数组套权值线段树、线段树套平衡树、分块(暴力数据结构)、线段树套\(vector\)等等都可以过掉这道题(汗)
例题
根据二逼平衡树的经验
用树状数组套动态开点权值线段树即可
方法一:像上面那个题一样,树状数组套动态开点权值线段树,只不过把查询第\(k\)小改为查询比一个数大的数目即可
方法二:三维偏序\(CDQ\)即可
3.CF1093E Intersection of Permutations
一眼看上去仿佛并没有什么思路
按照这道题,我们不仅需要找集合,还需要求出并集(难~)
因此我们换一种方法
我们考虑一个元素是不是都在这两个范围之内
那么我们把每一个数抽象为二维平面上的一个点,设\(P_{a_i}\)作为\(i\)这个元素在\(a\)排列中的位置,\(p_{b_i}\)为\(i\)这个元素在\(b\)这个排列中的位置,那么这个点的坐标即为\((p_{a_i},p_{b_i})\)。
操作一也就变成了一个二维数点问题
操作二就是将两个点的纵坐标互换
而两个维度的话一个放在内层,另一个放在外层维护即可
所以可以树状数组套权值线段树
树状数组维护的是前缀和,那么对于树状数组的每一个位置,我们都维护一个动态开点权值线段树,用来维护前缀里面所有出现的数。
修改的时候,跳\(lowbit\),然后在对应的线段树上修改。
查询的时候,先让区间左端点跳\(lowbit\),跳的过程中不断减去在权值线段树上对应区间出现的数的个数。
区间右端点也是跳\(lowbit\),只不过是跳的过程中是加而不是减。
(和P3759差不多)
这道题目无非两个操作:
1.单点修改
2.查询树上两点路径第\(k\)大
三种方法,时间复杂度依次递减:
1.对于一条链,我们用树剖+\(dfn\)序将它转化为多个区间第\(k\)大,求区间第\(k\)大,我们可以采用线段树套平衡树,需要二分答案+区间排名
\(O(n \space log^4n)\)
2.我们考虑方法一的弊端,就是线段树套平衡树没办法将区间第\(k\)大直接合并,必须二分答案
所以我们想将这个过程去掉,像上面一样
因此我们可以树剖+带修主席树
\(O(n\space log^3n)\)
3.还能不能再优化了呢?\(Of \space course\),上面的方法时间复杂度瓶颈在于树链剖分,那能不能不树剖了呢?
当然了,我们考虑这样的一个问题,之前讲主席树的时候讲到了这样的一道题目,P2633 Count on a tree,我们也是求的链上第\(k\)大,这道题中,我们用的主席树+树上差分的思想,那这道题能不能也这样呢?
当然也是可以啦。我们可以用\(u\)的主席树+\(v\)的主席树-\(lca\)的主席树-\(fa[lca]\)的主席树得到这段区间出现的数的个数,也就是说我们要维护每个点的主席树。
考虑到修改的时候,我们对一个点修改,实际上是对整个以这个点为根的子树产生了影响,而一颗子树的\(dfs\)序是连续的,我们转化成\(dfs\)序上的区间修改和单点查询问题。
我们再联系之前的树状数组,我们把这类问题变成了差分,同样,我们把这道题变成了\(dfs\)序上的差分主席树,也就是在\(dfn[x]\)加,在\(dfn[x]+size[x]\)减。
然后查询时\(O(\log n)\)地跳主席树来统计一个点的答案,再加上不断二分区间是\(O(\log n)\)的,总共的时间复杂度是\(O(n\log^2n)\)
从题面发现很显然是一道树套树的题(这不是废话吗)
那么我们用哪种树套树呢?
线段树套平衡树?
我们还需要二分答案,时间复杂度\(O(nlog^3n)\),瞬间爆炸。。。
区间线段树套权值线段树?
这不是跟上面那个一模一样嘛。。。
我们考虑一下我们的时间复杂度为什么会这个高?
树套树的基本时间复杂度一般都是\(O(nlog^2n)\),这个一般是优化不了的,那么我们发现,好像多二分了一个答案。
那么我们怎么把二分答案这个环节去掉呢?考虑二分答案实际上是对权值进行二分。
那么二分权值是不是线段树也可以做到?
于是我们选择用权值线段树套区间线段树,就免去了二分答案这个环节。。
那么之前在权值线段树上作为二分依据的\(size\),我们现在用在区间线段树上查询来获得。
时间复杂度为\(O(nlog^2n)\),这里为了空间能够开下,我们里层的区间线段树选择动态开点。
动态树之Link Cut Tree
动态树问题:维护森林的连通性。
而LCT就是解决动态树问题的一种方法。
其实LCT就是我们平时说的实链剖分。
重链剖分你们肯定都透彻。实链剖分学起来也不是很困难的。
那实链剖分就是把重链剖分的重边变成实边,轻边变成虚边。
由于操作需求,实虚链之间是会不断变化的,所以我们需要一个灵活的数据结构来维护。
当然是灵活的Splay了啊!!!
我们需要用Splay来维护实路径。
也就是说,我们会把所有用实边相连的点都放在同一颗Splay里面,这样我们就会有若干颗Splay Tree。
由于一个节点所连出去的实边只有一条,那么一颗Splay里面不同节点的深度也是不同的。
所以深度就取代了我们在普通平衡树里面的val来作为平衡的标准。
这里,我们的LCT时间复杂度是均摊\(O(logn)\)的。主要是取决于Splay的时间复杂度。
那么LCT有以下三个比较重要的性质:
-
每一颗Splay里面维护的都是一条在原树中从上到下严格递增的路径上的节点,中序遍历的深度必须严格递增。
-
每个节点都只能被包括在一颗Splay里面,即不存在两颗Splay存在相同的节点。
-
边分为实边和虚边,实边是会被包括在一棵Splay里面的,虚边是从一棵Splay指向另一颗Splay(这条边是后者Splay树中根节点和它(指整棵Splay树)
在原树中的父亲相连的边)对于实边,父亲儿子都互相认。而对于虚边,父不认子而子认父。
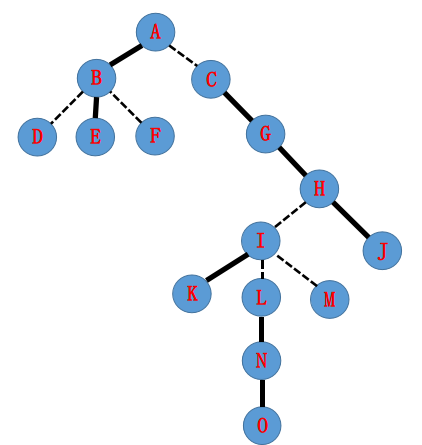
比如说一开始的实虚边是这样划分的。
那么对应到Splay上是怎么样的呢? 是这样的:
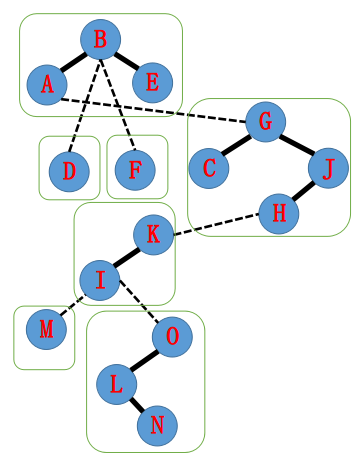
每一个绿框里面的节点在同一颗Splay里面。
Access
LCT最核心的操作,也是最让人难懂的操作了吧。
\(access(x)\),就是打通从x到原树的根节点的实路径,其实也就是把x到根上的所有节点都放到同一颗Splay里面,并且x节点必须是这颗Splay里面节点深度最大的,也就是x不能和它的任何一个儿子连实边。
那么现在举个例子来更好地理解一下:
我们现在要\(access(N)\),那么我们希望把实虚边划分成这样:
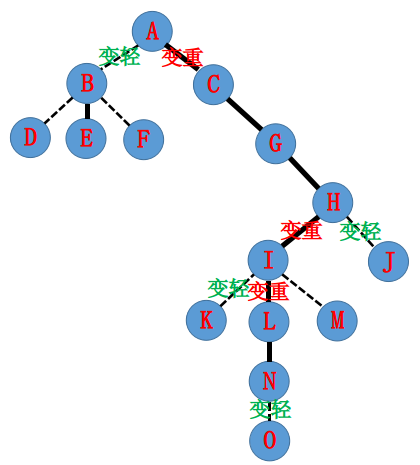
那么怎么实现呢?
我们需要一步步的往上拉。
首先,先\(splay(N)\),让它成为Splay的根,因为不能有深度比N更大的节点了,所以我们需要把节点深度比它大的右子树置为空,也就是\(N-O\)之间的边要变成虚边。
变成这样:
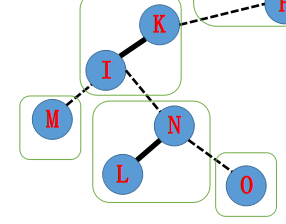
接着就类似于重链剖分的跳重链一样,我们不断的通过虚边来跳Splay。
对于现在来说的话,我们要跳到\(I\)这个节点,然后把它转到根,再把它的右子树置为N所在的Splay,就是\(I-N\)这条边变成实边。
然后变成这样:
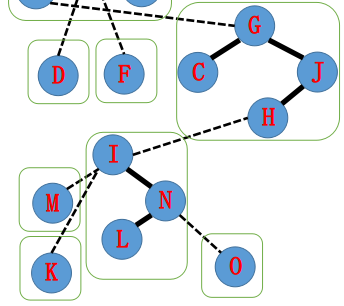
接着,我们跳到H这个节点,进行类似于上面的操作。
再变成这样:
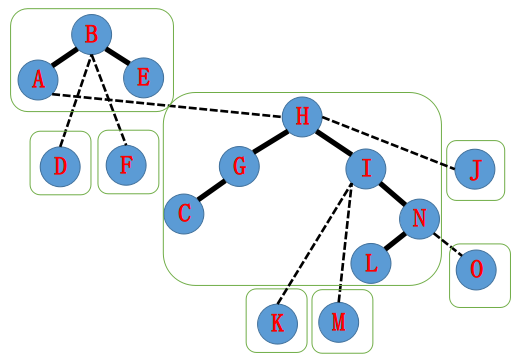
再跳到A,也是同样的操作,最后变成了这样:
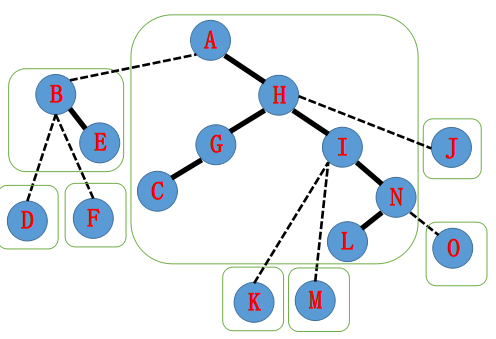
大功告成!!!
怎么样,是不是感觉很麻烦,但是代码只有一行。。。
其实就是splay,然后换右儿子,更新信息,跳虚边。。。
Makeroot
其实有的时候,我们需要拉出一条两个节点之间的路径,但是如果两个节点都不是根节点的话,就不满足性质1了。
所以我们有了makeroot这个操作,\(makeroot(x)\)就是把x变成原树的根了,那么就可以从另一个节点拉边了。
怎么实现呢?
我们考虑,如果把这个节点变成根节点的话,为了满足性质1,从x到根的路径上的深度需要全部反过来。
所以,我们先打通x到根的路径,再把x splay到根,再把整颗Splay翻转过来(翻转的话,可以参考文艺平衡树)。
Findroot
\(findroot(x)\)就是找到x所在的原树的根节点,一般是用来判断两个点是不是在同一颗原树中。
先打通路径,然后把x splay到根,然后找最左节点,就是原树的根节点(因为深度最小嘛)。
Split
\(split(x,y)\)拉出一条从x到y的路径,很简单吧。
把其中一个变成根,让另一个access就行了。再splay上去,就可以统计一些信息了。
Link
LCT怎么能没有link操作呢,就是连一条边。
我们需要先判断一下是否已经连边了。
如果没有的话,让一个节点成为所在原树的根节点,然后直接认爹就行了(因为不在同一颗Splay里面,不需要父亲认儿子)。
Cut
删掉一条边。
我们也需要判断一下是否本来就没有边。
如果有的话,可以先拉出来一条从x到y的路径,然后判断x和y是否直接相连,如果直接相连,直接断边,父子不相认。
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
int n, val[N], m, s[N], ch[N][2], fa[N], tag[N], sta[N];
inline int read()
{
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
void pushr(int x) {swap(ch[x][0], ch[x][1]); tag[x] ^= 1;}
void pushup(int x) {s[x] = (s[ch[x][0]] ^ s[ch[x][1]] ^ val[x]);}
int nrt(int x) {return ch[fa[x]][0] == x || ch[fa[x]][1] == x;}
void pushdown(int x) {if(!tag[x]) return; if(ch[x][0]) pushr(ch[x][0]); if(ch[x][1]) pushr(ch[x][1]); tag[x] = 0;}
int isr(int x) {return ch[fa[x]][1] == x;}
void rot(int x)
{
int y = fa[x], z = fa[y], k = isr(x), w = ch[x][!k];
if(nrt(y)) ch[z][isr(y)] = x;
fa[x] = z; fa[y] = x; ch[x][!k] = y; ch[y][k] = w;
if(w) fa[w] = y;
pushup(y); pushup(x);
}
void splay(int x)
{
int y = x, top = 0; sta[++ top] = y;
while(nrt(y)) sta[++ top] = y = fa[y];
while(top) pushdown(sta[top --]);
while(nrt(x))
{
if(nrt(fa[x])) rot((isr(x) == isr(fa[x])) ? fa[x] : x);
rot(x);
}
pushup(x);
}
void access(int x) {int y = 0; while(x) splay(x), ch[x][1] = y, pushup(x), x = fa[y = x];}
void makeroot(int x) {access(x); splay(x); pushr(x);}
void split(int x, int y) {makeroot(x); access(y); splay(y);}
int findroot(int x) {access(x); splay(x); while(ch[x][0]) pushdown(x), x = ch[x][0]; return splay(x), x;}
void link(int x, int y) {makeroot(x); if(findroot(y) != x) fa[x] = y;}
void cut(int x, int y) {makeroot(x); if(findroot(y) != x || ch[y][0] || fa[y] != x) return; fa[y] = ch[x][1] = 0; pushup(x);}
int main()
{
n = read(); m = read();
for(int i = 1; i <= n; i ++) val[i] = read();
int opt, x, y;
while(m -- > 0)
{
opt = read(); x = read(); y = read();
if(opt == 0) split(x, y), printf("%d\n", s[y]);
else if(opt == 1) link(x, y);
else if(opt == 2) cut(x, y);
else if(opt == 3) splay(x), val[x] = y;
}
fclose(stdin);
fclose(stdout);
return 0;
}
例题
甚至连板子都不如。。。(还是写写练练手感吧。)
这个题还有点意思。我们还需要区间加和区间乘。想到了什么呢?
想一下我们曾经在哪道题上维护过类似的操作。
没错,就是线段树2啊。
我们还是采用和线段树2相同的套路。对于乘法和加法,我们让乘法优先,这样可以让精度损失降到最小。
我们现在要维护的标记除了翻转标记,还有加法标记和乘法标记,可以一起下放,对于时间复杂度没有什么太大的影响。然后就是一些细节问题了。
这不LCT裸题嘛
我知道大家之前都是用分块写的,其实这题也可以用\(LCT\)写,LCT被分块撵爆了
大家好好观察一下就很容易发现怎么用\(LCT\)来维护。
我们考虑,添加一个虚拟节点,这个节点就表示绵羊被弹飞了,那么所有跳之后会超出边界的点都要向这个节点连边。剩下的该向谁连就向谁连就行了。
对于查询操作,我们怎么办?
我们发现我们查询的实质就是这个点到虚拟节点中一共经过了多少条边,所以我们拉出一条路径,然后统计一下这个路径上一共有多少个节点,然后再减一就行了。
那么修改操作呢?
其实就是断了一条边,然后又连了一条边。
然后就没了。
那我们先看看这些操作吧。看能不能发现些什么。
- 操作1,把\(x\)到根染上同一种颜色,怎么跟\(access\)那么像啊。
莫非?我们灵机一动,决定用\(Splay\)来维护同一个颜色的集合。 - 操作2,\(x\)到\(y\)的权值,莫非直接\(split\)?然而,你的\(Splay\)是维护同一个颜色,你的\(LCT\)现在根本就不支持除了\(access\)之外的任何东西了。那怎么办呢?
不慌,我们考虑他是树上一条路径,我们考虑之前求两点间距离是怎么求的,是不是树上差分?那这个操作我们也可以用树上差分来实现,具体就是:我们设\(f[x]\)表示x这个节点到根节点的权值,那么可以得到\(val[x][y] = f[x] + f[y] - 2 * f[lca(x,y)] + 1\),加一是因为lca这个点的颜色会被多减一次。
3. 操作3,众所周知,LCT擅长维护一条链,对于子树内的操作它几乎是无能为力的。我们考虑一颗子树内的\(dfs\)序是连续的,所以我们可以用\(dfs\)序上建线段树来维护。
那么我们怎么维护这个\(f\)值呢?
我们考虑\(f\)值只有在进行\(access\)时会发生变化,连边时\(f\)值会减一,断边时\(f\)值会加一。
留个有意思的小习题:
其他
融合树&划分树&支配树
有兴趣的同学请自学...
K-DTree&珂朵莉树(ODT)&Kruskal重构树&虚树&李超线段树
由于时间问题,我选择——甩锅,详见\(wljss\)博客园




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步