网络流
网络流
网络流简介(不一样的简介,一样的没用。。。)
网络
网络指一个有向图\(G = (V,E)\)
每条边\((u,v)\in E\) 都有一个权值\(c(u,v)\),称之为容量
其中有两个特殊的点:源点 \(s \in V\)和汇点\(t \in V\)
流
设\(f(u,v)\)定义在二元组\((u \in V,v \in V)\)上的实体函数且满足
1、容量限制: \(f[u,v]<=c[u,v]\)
2、反对称性:\(f[u,v] = - f[v,u]\)
3、流量平衡: 对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。
那么\(f\)称为网络\(G\)的流函数,对于\((u,v) \in E\),\(f(u,v)\)称为边的流量,\(c(u,v) - f(u,v)\)称为边的剩余流量。
整个网络的流量为\(\displaystyle\sum_{(s,v) \in E}f(u,v)\),即从源点发出的所有流量之和。
网络流的常见问题
最大流
我们有一张图,要求从源点流向汇点的最大流量(可以有很多条路到达汇点),就是我们的最大流问题。
最小费用最大流
最小费用最大流问题是这样的:每条边都有一个费用,代表单位流量流过这条边的开销。我们要在求出最大流的同时,要求花费的费用最小。
最小割
割其实就是删边的意思,当然最小割就是割掉\(X\)条边来让\(S\)跟\(T\)不互通。我们要求\(X\)条边加起来的流量总和最小。这就是最小割问题。
...
最大流
Ford-Fulkerson 增广路算法
该方法通过寻找增广路来更新最大流,有 \(EK,dinic,SAP(由于有ISAP,我们就不讲啦),ISAP\) 等算法。
残量网络
首先一条边的剩余流量为\(c_{f}(u,v)\),表示这条边的容量与流量之差,即\(c_{f}(u,v) = c(u,v) - f(u,v)\)。
残存网络\(G_{f}\)是网络\(G\)中所有结点和剩余流量大于0的边构成的子图。
\(G_{f} = (V_{f} = V,E_{f} = {(u,v) \in E,c_{f}(u,v) > 0})\)。
注意,剩余流量大于0的边包括剩余流量大于0的反向边。
对于每条边 \((u,v,w)\) ,建一条相应的反向边 \((v,u,0)\)
至于为啥,相信就不用我解释了吧。。。
增广路
若在原图中一条从\(s\)到\(t\)的路径上的所有边的剩余流量都大于0,这条路被称为增广路。(在残存网络中存在一条从\(s\)到\(t\)的路径)。
Edmond-Karp 算法(EK 算法)
算法执行时,从\(s\)开始\(bfs\),看看到\(t\)最多能流多少,对于每个节点记录它的前驱节点,如果到\(t\)的流量不为0,那么从\(t\)回溯回\(s\),将每条边的容量减去流量,其反向边的容量加上流量,然后把答案加上所有回溯到的边的流量;否则停止执行,返回结果。最坏复杂度 \(O(n*m^2)\) 。
inline bool bfs(int s, int t)
{
while(q.size()) q.pop();
for(int i = 1; i <= n; ++i) fa[i] = 0;
fa[s] = 1; low[s] = inf;
q.push(s);
while(q.size())
{
int a = q.front();
if(a == t) return true;
q.pop();
for(int i = head[a]; i; i = e[i].nxt)
{
int to = e[i].to;
if(e[i].cap > 0 && fa[to] == 0)
{
fa[to] = i;
low[to] = min(e[i].cap, low[a]);
q.push(e[i].to);
}
}
}
return false;
}
inline int EK(int t, int s)
{
int ans = 0;
while(bfs(s, t))
{
for(int i = t; i; i = e[fa[i]].from)
{
if(i == s) break;
int j = fa[i];
e[j].cap -= low[t];
e[j ^ 1].cap += low[t];
}
ans += low[t];
}
return ans;
}
Dinic 算法
1.\(bfs\)构建分层图网络
2.\(dfs\)进行多路增广
3.重复以上过程直至汇点\(t\)无法与源点\(s\)联通
最坏复杂度\(O(n ^ {2} *m)\)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int inf = 2147483647;
queue<int> q;
int flow;
int n,m,s,t,tot = 1,dis[10005],head[10005],ans;
struct node{
int to,nex,val;
}a[200005];
void add(int x,int y,int z)
{
a[++ tot].to = y;
a[tot].nex = head[x];
a[tot].val = z;
head[x] = tot;
}
bool bfs()
{
while(!q.empty()) q.pop();
memset(dis,0,sizeof(dis));
q.push(s); dis[s] = 1;
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(!dis[y] && a[i].val)
{
dis[y] = dis[x] + 1;
q.push(y);
if(y == t) return 1;
}
}
}
return 0;
}
int dfs(int x,int want)
{
if(x == t || ! want) return want;
int f = 0,get = 0;
for(int i = head[x];i && want;i = a[i].nex)
{
int y = a[i].to;
if(dis[y] == dis[x] + 1 && a[i].val)
{
f = dfs(y,min(want,a[i].val));
if(f == 0)
{
dis[y] = 0;
continue;
}
a[i].val -= f; a[i ^ 1].val += f;
want -= f; get += f;
}
}
return get;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i = 1;i <= m;i ++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z); add(y,x,0);
}
while(bfs()) while(flow = dfs(s,inf)) ans += flow;
printf("%d\n",ans);
return 0;
}
当前弧优化
我们定义一个数组\(cur\)记录当前边(弧)(功能类比邻接表中的\(head\)数组,只是会随着\(dfs\)的进行而修改),每次我们找过某条边(弧)时,修改\(cur\)数组,改成该边(弧)的编号,那么下次到达该点时,会直接从\(cur\)对应的边开始(也就是说从\(head\)到\(cur\)中间的那一些边(弧)我们就不走了)。
但是每次\(dfs\)前要
for(int i = 1;i <= n;i ++) cur[i] = head[i];
核心:
for(int &i = cur[x];i && want;i = a[i].nex)
ISAP算法
跟\(Dinic\)算法像的一批。。。用\(d[i]\)数组表示点\(i\)到汇点\(t\)的最短距离,初始化\(d[t] = 0,d[i \in E\mbox{&}i != t] = n + 1\),那么优化在哪里捏?主要是:
1.如果源点\(s\)距离汇点\(t\)的最短路径长度大于等于\(n\),说明\(s\)与\(t\)肯定不互相联通,所以结束算法。
2.记录一下每一层节点的个数,如果某一层结点个数为0,则说明该层出现了断层,则直接停止增广即可,可以直接将\(d[s]\)更改为\(n + 1\)。
3.那么在\(dfs\)过程中如何修改\(deepth\)捏?将这个节点的\(deepth\)更新成与它相邻的高度最小的节点的高度\(+1\)。
最坏复杂度\(O(n ^2 *m)\)
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int N = 100005;
const int inf = 0x3f3f3f3f;
queue<int> q;
int n,m,s,t,tot = 1,head[N],mxflow,d[N],c[N];
struct node{int to,nex,val;}a[N << 1];
inline int read()
{
int x = 0,f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}
return x * f;
}
void add(int x,int y,int z)
{
a[++ tot].to = y;
a[tot].val = z;
a[tot].nex = head[x];
head[x] = tot;
}
void bfs()
{
for(int i = 1;i <= n;i ++) d[i] = n + 1;
d[t] = 1; q.push(t);
while(!q.empty())
{
int x = q.front(); q.pop();
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(d[y] == n + 1 && a[i].val == 0)
{
d[y] = d[x] + 1;
q.push(y);
}
}
}
}
int dfs(int x,int want)
{
if(x == t || !want) return want;
int f = 0,get = 0,mn = n + 1;
for(int i = head[x];i && want;i = a[i].nex)
{
int y = a[i].to;
if(d[y] == d[x] - 1 && a[i].val)
{
f = dfs(y,min(want,a[i].val));
want -= f; get += f;
a[i].val -= f; a[i ^ 1].val += f;
if(!want) return get;
}
if(a[i].val) mn = min(mn,d[y] + 1);
}
c[d[x]] --;
if(!c[d[x]] && mn != d[x]) d[s] = n + 1;
c[d[x] = mn] ++;
return get;
}
int main()
{
n = read();m = read();s = read();t = read();
for(int i = 1,x,y,z;i <= m;i ++)
{
x = read();y = read();z = read();
add(x,y,z); add(y,x,0);
}
bfs();
for(int i = 1;i <= n;i ++) c[d[i]] ++;
while(d[s] < n + 1) mxflow += dfs(s,inf);
printf("%d\n",mxflow);
return 0;
}
预流推进
最高标号预流推进(HLPP)
算法步骤:
1.先从\(t\)到\(s\)反向\(bfs\),使每一个点都有一个初始高度。
2.从\(s\)开始向外推流,将有余流的点放入优先队列。
3.不断从优先队列里取出高度最高的点进行推流。
4.若推完还有余流,更新高度标号并重新将其压入队列。
5.当优先队列为空时结束算法,最大流即为\(t\)的余流。
优化:
1.利用优先队列使得每次推流都是高度最高的点,以此减少推流以及重新标号的次数。
2.和\(ISAP\)一样的优化,如果某个高度不存在,将所有比该高度高的节点标记为不可达(使它的高度为\(n + 1\),这样就会直接向\(s\)推流,而不会向\(t\)推流)。
时间复杂度\(O(n ^2 * \sqrt m)\),但是\(HLPP\)常数较大,在纯随机数据(模板题)下跑的还没有\(ISAP\)快。
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int N = 1505;
const int inf = 0x3f3f3f3f;
queue<int> Q;
int n,m,s,t,head[N],tot = 1,d[N],c[N],v[N],e[N];
//e:每个点的总流入-总流出
struct data{int to,nex,val;}a[3000005];
struct cmp
{
bool operator () (int a,int b)const
{
return d[a] < d[b];
}
};
priority_queue<int,vector<int>,cmp> q;
inline int read()
{
int x = 0,f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}
return x * f;
}
void add(int x,int y,int z)
{
a[++ tot].to = y;
a[tot].val = z;
a[tot].nex = head[x];
head[x] = tot;
}
void bfs()
{
for(int i = 1;i <= n;i ++) d[i] = n + 1;
d[t] = 0; Q.push(t); v[t] = 1;
while(!Q.empty())
{
int x = Q.front(); Q.pop(); v[x] = 0;
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(a[i].val == 0 && d[y] > d[x] + 1)
{
d[y] = d[x] + 1;
if(!v[y]){Q.push(y);v[y] = 1;}
}
}
}
}
void push(int x)
{
for(int i = head[x],y,mn;i;i = a[i].nex)
{
y = a[i].to;
if(a[i].val && d[x] == d[y] + 1)
{
mn = min(e[x],a[i].val);
e[x] -= mn; e[y] += mn;
a[i].val -= mn; a[i ^ 1].val += mn;
if(!v[y] && y != s && y != t)
{
q.push(y);
v[y] = 1;
}
if(e[x] == 0) break;
}
}
}
void change(int x)
{
d[x] = inf;////!!!!
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(a[i].val && d[x] > d[y] + 1) d[x] = d[y] + 1;
}
}
int HLPP()
{
bfs();
if(d[s] == n + 1) return 0; d[s] = n;
for(int i = 1;i <= n;i ++) c[d[i]] ++;
for(int i = head[s],y;i;i = a[i].nex)
{
y = a[i].to;
if(a[i].val)
{
e[s] -= a[i].val;
e[y] += a[i].val;
a[i ^ 1].val += a[i].val;
a[i].val = 0;
if(y != s && y != t && !v[y])
{
q.push(y);
v[y] = 1;
}
}
}
while(!q.empty())
{
int x = q.top(); q.pop(); v[x] = 0; push(x);
if(e[x])
{
c[d[x]] --;
if(!c[d[x]])
{
for(int i = 1;i <= n;i ++)
if(i != s && i != t && d[i] > d[x] && d[i] < n + 1)//d[i]<n+1快的一批!(不知道为啥。。反正不写会卡着边界过。。)
d[i] = n + 1;
}
change(x);
c[d[x]] ++;
q.push(x); v[x] = 1;
}
}
return e[t];
}
int main()
{
n = read();m = read();s = read();t = read();
for(int i = 1,x,y,z;i <= m;i ++)
{
x = read();y = read();z = read();
add(x,y,z); add(y,x,0);
}
printf("%d\n",HLPP());
return 0;
}
注意:
以上我们所说的时间复杂度大多都是最高时间复杂度,一般情况下是远远跑不满这个时间复杂度的。
例题:
。。最大流模板题,由于板子已给出,这里只给出主函数(以下代码同样不再给出板子)
int main()
{
scanf("%d%d",&m,&n);
s = 0,t = n + 1;
int x,y;
while(scanf("%d%d",&x,&y))
{
if(x == -1 && y == -1) break;
add(x,y,1);add(y,x,0);
}
for(int i = 1;i <= m;i ++){add(s,i,1);add(i,s,0);}
for(int i = m + 1;i <= n;i ++){add(i,t,1);add(t,i,0);}
dinic();
if(tot == 0)
{
printf("No Solution!\n");
return 0;
}
printf("%d\n",ans);
for(int i = 2;i <= tot;i += 2)
{
if(a[i].to != s && a[i ^ 1].to != s)
if(a[i].to != t && a[i ^ 1].to != t)
if(a[i ^ 1].flow > 0)
printf("%d %d\n",a[i ^ 1].to,a[i].to);
}
}
考虑如何连边呢?
我们对每个点进行拆点,若\(b\)可以接在\(a\)之后,我们就由\(a\)向\(b'\)连一条容量为1的边表示\(b\)可以接在\(a\)的后面,那么对于一个点拆成的两个点\(i\)和\(i'\),我们由\(s\)向\(i\)连一条容量为1的边,由\(i'\)向\(t\)连一条容量为1的边表示每个点只能选择与被选择至多各一次。
接下来观察本题,对于一个新进来的编号的球,他有两种情况:
1.与某个球相连 2.独立门户
首先与\(s\)和\(t\)连边是必不可少的啦,由于新加进来的点一定是当前编号最大的,所以它只有可能会待在已有的点的后面,所以我们考虑枚举平方数并由相应的点向新点连边。连完边之后,我们就去增广,若能增广出一条新路径,那么说明这个点可以合法的接在一个点的后面,否则说明不可以,需要新开一个柱子。重复以上过程直至柱子数大于\(n\)为止。
统计方案只需要在跑最大流的过程中记录一下即可。
注意,以上会循环到不合法为止,所以合法的球数为到结束时的球数\(-1\)。
最后输出方案即可。
int dfs(int x,int want)
{
if(x == t || !want) return want;
int f = 0,get = 0;
for(int i = head[x];i && want;i = a[i].nex)
{
int y = a[i].to;
if(d[y] == d[x] + 1 && a[i].val)
{
f = dfs(y,min(want,a[i].val));
if(!f)
{
d[y] = 0;
continue;
}
a[i].val -= f; a[i ^ 1].val += f;
want -= f; get += f;
if(y != t) nx[x >> 1] = y >> 1;//
if(!want) return get;
}
}
return get;
}
int dinic()
{
int k = 0,flow;
while(bfs()) while(flow = dfs(s,inf)) k += flow;
return k;
}
int main()
{
n = read();
s = 0;t = 5000;
while(now <= n)
{
num ++;
add(s,(num << 1),1); add((num << 1),s,0);
add((num << 1 | 1),t,1); add(t,(num << 1 | 1),0);
for(int i = sqrt(num) + 1;i * i < 2 * num;i ++)
add(((i * i - num) << 1),(num << 1 | 1),1),add((num << 1 | 1),((i * i - num) << 1),0);
int k = dinic();
if(!k) em[++ now] = num;
}
printf("%d\n",-- num);
for(int i = 1;i <= n;i ++)
{
int x = em[i];
while(x != 0)
{
printf("%d ",x);
x = nx[x];
}
printf("\n");
}
return 0;
}
和二分图最大匹配像的一批。。。
建边:
我们从源点向各个单位连一条容量为该单位人数的边,表示每个单位最多匹配与该单位的人数相等的次数,从每个圆桌向汇点连一条容量为该圆桌可容纳人数的边,意义同上,那么对于单位与圆桌之间我们如何连边呢?我们从每个单位分别向每个圆桌连一条容量为1的边,表示每个单位与每个圆桌最多匹配一次。最后跑最大流就好啦。
判断是否合法:
若最后最大流等于每个单位的总人数和,则合法,否则不合法。
输出方案:暴力判断就好。。
int main()
{
m = read();n = read();
s = 0;t = m + n + 1;
for(int i = 1,x;i <= m;i ++)
{
x = read(); sum += x;
add(s,i,x); add(i,s,0);
}
for(int i = 1,x;i <= n;i ++)
{
x = read();
add(i + m,t,x); add(t,i + m,0);
}
for(int i = 1;i <= m;i ++)
for(int j = 1;j <= n;j ++)
{
add(i,j + m,1); add(j + m,i,0);
e[i][j] = tot;
}
if(dinic() == sum) printf("1\n");
else{printf("0\n");return 0;}
for(int i = 1;i <= m;i ++,printf("\n"))
for(int j = 1;j <= n;j ++)
if(a[e[i][j]].val != 0) printf("%d ",j);
return 0;
}
显然,我们由源点向试题类型连一条容量为该试题类型所需试题数量的边代表要选出多少套该类型的试题,由试题向汇点连一条容量为1的边代表每套试题只能使用一次,然后在可以匹配的试题类型与试题之间连一条容量为1的边。然后跑一遍最大流,若最大流结果等于每种试题类型所需试题数的总和则可行,否则不可行。输出方案时暴力判断即可。。
int main()
{
k = read();n = read();
s = 0;t = k + n + 1;
for(int i = 1,x;i <= k;i ++)
{
x = read(); sum += x;
add(s,i,x); add(i,s,0);
}
for(int i = 1,x;i <= n;i ++)
{
x = read();
add(i + k,t,1); add(t,i + k,0);
for(int j = 1,y;j <= x;j ++)
{
y = read();
add(y,i + k,1); add(i + k,y,0);
e[y][i] = tot;
}
}
if(Dinic() != sum){printf("No Solution!\n");return 0;}
for(int i = 1;i <= k;i ++,printf("\n"))
{
printf("%d: ",i);
for(int j = 1;j <= n;j ++) if(a[e[i][j]].val) printf("%d ",j);
}
return 0;
}
对于这道题的第一问,显然\(dp\)就好了。设\(f[i]\)表示以\(i\)结尾的最长不下降子序列的长度,\(O(n ^ 2)\)转移即可。。令\(mx = max_{i=1}^{n}f[i]\)。
对于第二问,我们用网络流解决,首先由于题目中限制了每个数字只能使用一次,我们想到了拆点,将每个点\(i\)拆成两个点\(i\)和\(i + n\),并从\(i\)向\(i + n\)连一条容量为1的边表示该数字只能使用一次,那么为了保证我们选出的数字组成的不下降子序列的长度为\(mx\),我们从源点向\(f[i] == 1\)的点\(i\)连一条容量为1的边,从\(f[i] == mx\)的点\(i\)向汇点连一条容量为1的边,对于中间部分我们从满足\(i>=j\mbox{&&}x[i]>=x[j]\mbox{&&}f[i]==f[j]+1\)的点\(j\)向点\(i\)连一条容量为1的边,最后跑最大流就好了。
对于第三问,我们仿照第二问就好,但是需要将从源点到\(1\)、从\(1\)到\(1+n\)、从\(n\)到\(2*n\)、从\(2*n\)到汇点的边的容量改为\(inf\)表示\(x[1]\)和\(x[n]\)可以使用多次,然后跑最大流就好了。
int main()
{
n = read(); s = 0;t = 2 * n + 1;
for(int i = 1;i <= n;i ++) x[i] = read();
for(int i = 1;i <= n;i ++)
{
for(int j = 1;j < i;j ++) if(x[i] >= x[j]) f[i] = max(f[i],f[j] + 1),mx = max(mx,f[i]);
if(!f[i]) f[i] = 1;
}
printf("%d\n",mx);
for(int i = 1;i <= n;i ++)
{
if(i == 1 || i == n) {add1(i,i + n,1);add2(i,i + n,inf);}
else {add1(i,i + n,1);add2(i,i + n,1);}
}
for(int i = 1;i <= n;i ++)
{
if(f[i] == 1)
{
if(i == 1) {add1(s,i,1);add2(s,i,inf);}
else {add1(s,i,1);add2(s,i,1);}
}
if(f[i] == mx)
{
if(i == n) {add1(i + n,t,1);add2(i + n,t,inf);}
else {add1(i + n,t,1);add2(i + n,t,1);}
}
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j < i;j ++)
if(x[i] >= x[j] && (f[i] == f[j] + 1))
add1(j + n,i,1),add2(j + n,i,1);
printf("%d\n",Dinic1());
if(n != 1) printf("%d\n",Dinic2());
else printf("1\n");
return 0;
}
题目中已经给了解法了,但是我认为这太草率了。。。(主要是我看了第一篇题解不能白看呀),所以我再说两句。
首先题意应该没有问题吧,就是让求出能包含所有点的最少路径条数,由于规定顶点不相交,也就是说每个点只能出现在一条路径中,因此我们考虑拆点,将每个点\(i\)拆成\(i\)和\(i+n\)两个点,从源点向\(i\)连一条容量为1的边表示它只能指向一个点,从\(i+n\)向汇点连一条容量为1的边只能有一个点指向它。
我们先假设所有的点都是零散的,那么就有\(n\)条路径,但是由于一些点之间是连有边的,所以我们可以合并这些点,那么我们每合并两个点就会减少一条路径,所以我们现在只需要求出有多少个“两个点”是可以合并的就好了。
那么我们对于\((u,v)\in E\)从 \(u\) 向 \(v + n\) 连一条容量为1的边表示这两个点可以合并,那么我们跑一遍最大流后就可以求出有多少个“两个点”是可以合并的,所以最终的路径条数就是\(n-mxflow\)。
输出路径:我们可以记录一下任意有边相连的两点之间的边在网络中的编号,判断一下这条边的反向边是否有流量,若有则说明这两点合并了,设这条边是\((u,v)\),那么我们就令\(u\)的下一个点是\(v\),最后判断一下入度为0的点就好了。
void get_ans(int x)
{
while(x != 0)
{
printf("%d ",x);
x = nxt[x];
}
}
int main()
{
n = read();m = read();
s = 0;t = 2 * n + 1;
for(int i = 1;i <= n;i ++)
{
add(s,i,1); add(i,s,0);
add(i + n,t,1); add(t,i + n,0);
}
for(int i = 1,x,y;i <= m;i ++)
{
x = read();y = read();
add(x,y + n,1); add(y + n,x,0);
e[x][y] = tot;
}
Dinic();
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= n;j ++)
if(a[e[i][j]].val)
{
nxt[i] = j;
in[j] ++;
}
for(int i = 1;i <= n;i ++) if(!in[i]) get_ans(i),puts("");
printf("%d\n",n - mxflow);
return 0;
}
首先对于无解的情况,我们可以用并查集维护一下,对于每个飞船能到的所有太空站分别进行合并,若最后地球和月球不在一个联通块中,则无解,输出0就\(OK\)啦。
那么对于一般情况,我们如何建边呢?我们可以以时间分层,以地球为源点,以月球为汇点,从每个飞船\(i\)在\(t\)时刻所在的太空站向它\(t+1\)时刻所在的太空站连一条容量为\(p[i]\)的边,表示可以传送这些人过去。但是题目中也说了,人在太空船停靠站是可以上下的,而且太空站可以容纳无限多的人,所以我们再从\(t\)时刻的每一个太空站向\(t+1\)时刻的该太空站连一条容量为\(inf\)的边。
每增加单位时间就尝试增广,当\(mxflow>=k\)时结束算法,输出当前时刻。
int find(int x){return f[x] == x ? x : f[x] = find(f[x]);}
void merge(int x,int y)
{
int xx = find(x),yy = find(y);
if(xx == yy) return;
f[xx] = yy;
}
int main()
{
n = read();m = read();k = read();
s = 0;t = N - 5;
for(int i = 1;i <= n + 1;i ++) f[i] = i;
for(int i = 1;i <= m;i ++)
{
p[i] = read();num[i] = read();
for(int j = 0;j < num[i];j ++)
{
g[i][j] = read();
if(g[i][j] == -1) g[i][j] = n + 1;
if(j) merge(g[i][j],g[i][j - 1]);
}
}
if(find(0) != find(n + 1)){printf("0\n");return 0;}
for(int ans = 1; ;ans ++)
{
for(int i = 1;i <= m;i ++)
{
int x = g[i][(ans - 1) % num[i]],y = g[i][ans % num[i]];
if(x == n + 1) x = t;
else if(x == 0) x = s;
else x = (ans - 1) * n + x;
if(y == n + 1) y = t;
else if(y == 0) y = s;
else y = ans * n + y;
add(x,y,p[i]); add(y,x,0);
}
for(int i = 1;i <= n;i ++) {add((ans - 1) * n + i,ans * n + i,inf);add(ans * n + i,(ans - 1) * n + i,0);}
if(Dinic() >= k){printf("%d\n",ans);return 0;}
}
return 0;
}
费用流
给定一个网络\(G = (V,E)\),每条边除了有容量限制\(c(u,v)\),还有一个费用\(w(u,v)\)
当\((u,v)\)的流量为\(f(u,v)\)时,需要花费\(f(u,v) * w(u,v)\)
\(w\)也满足斜对称性,即\(w(u,v) = -w(v,u)\)
则该网络中总花费最小的最大流成为最小费用最大流
普通算法
没什么好说的。。。
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
queue<int> q;
const int inf = 1528474639;
int n,m,s,t,tot = 1,head[5005],dis[5005],flow[5005];
int Cost,Flow,pre[5005],last[5005];
bool vis[5005];
struct node{
int to,nex,val,cost;
}a[100005];
#define RI register int
void add(RI x,RI y,RI z,RI w)
{
a[++ tot].to = y;
a[tot].nex = head[x];
a[tot].val = z;
a[tot].cost = w;
head[x] = tot;
}
bool spfa()
{
RI i,x,y;
for(i = 1;i <= n;++ i) dis[i] = flow[i] = inf;
q.push(s); vis[s] = 1; pre[t] = -1; dis[s] = 0;
while(!q.empty())
{
x = q.front(); q.pop(); vis[x] = 0;
for(i = head[x];i;i = a[i].nex)
{
y = a[i].to;
if(a[i].val && dis[y] > dis[x] + a[i].cost)
{
dis[y] = dis[x] + a[i].cost;
pre[y] = x; last[y] = i;
flow[y] = min(flow[x],a[i].val);
if(!vis[y]) q.push(y),vis[y] = 1;
}
}
}
return pre[t] != -1;
}
void mcmf()
{
RI now;
while(spfa())
{
now = t;
Cost += dis[t] * flow[t];
Flow += flow[t];
while(now != s)
{
a[last[now]].val -= flow[t];
a[last[now] ^ 1].val += flow[t];
now = pre[now];
}
}
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(RI i = 1,x,y,z,w;i <= m;++ i)
{
scanf("%d%d%d%d",&x,&y,&z,&w);
add(x,y,z,w); add(y,x,0,-w);
}
mcmf();
printf("%d %d\n",Flow,Cost);
return 0;
}
ZKW费用流
最短路算法保证在算法结束时,对于任意边\((i,j)\)满足①\(d_j<=d_i+c_{ij}\),且②对于每个\(j\)至少存在一个\(i\)使得等号成立,算法结束后,恰好在最短路上使得等号成立。而在最小费用最大流中我们就沿最短路进行增广,增广使得部分边不再有剩余流量,不会破坏①,但是可能会破坏②,在一般的费用流中,我们每次重新使用\(spfa\)来重新计算\(d\),但这无疑是一种浪费,所以我们通过\(dfs\)来修改\(d\)使得②成立。
我们令\(d_i\)表示点\(i\)到\(t\)的最短距离,\(v_i\)表示是否能从\(s\)扩展到\(i\)(每次只扩展剩余流量大于0且满足距离约束的边)。
一次增广之后,\(d_i\)理应扩大,扩大多少呢?令\(\delta=min(d_j+c_{ij}-d_i),v_i = 1 \mbox{&&} v_j = 0\mbox{&&}a[i].val>0\),则\(d_i\)应该增大\(\delta\),而且与\(s\)联通的部分应整体抬高\(\delta\),所以我们就这样修改就好啦。
一般情况下是不会卡普通费用流的,但是,谁说的准呢。。。
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 5005;
const int inf = 0x3f3f3f3f;
int n,m,s,t,v[N],head[N],mncost,mxflow,d[N],tot = 1;
struct node{int to,nex,val,cost;}a[5000005];
inline int read()
{
int x = 0,f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}
return x * f;
}
void add(int x,int y,int z,int w)
{
a[++ tot].to = y;
a[tot].nex = head[x];
a[tot].val = z;
a[tot].cost = w;
head[x] = tot;
}
int aug(int x,int flow)//增广
{
v[x] = 1;
if(x == t) return flow;
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(!v[y] && a[i].val && d[x] == d[y] + a[i].cost)
{
int f = aug(y,min(a[i].val,flow));
if(!f) continue;
a[i].val -= f; a[i ^ 1].val += f;
return f;
}
}
return 0;
}
bool modlabel()//修改高度
{
int tmp = inf;
for(int i = 1;i <= n;i ++)
{
if(!v[i]) continue;
for(int j = head[i];j;j = a[j].nex)
{
int y = a[j].to;
if(v[y] || !a[j].val) continue;
tmp = min(tmp,d[y] + a[j].cost - d[i]);
}
}
if(tmp == inf) return 1;
for(int i = 1;i <= n;i ++) if(v[i]) v[i] = 0,d[i] += tmp;
return 0;
}
void ZKW()
{
int flow;
while(1)
{
while(flow = aug(s,inf))
{
mxflow += flow;
mncost += flow * d[s];
for(int i = 1;i <= n;i ++) v[i] = 0;
}
if(modlabel()) break;
}
}
int main()
{
n = read();m = read();s = read();t = read();
for(int i = 1,x,y,z,w;i <= m;i ++)
{
x = read();y = read();z = read();w = read();
add(x,y,z,w); add(y,x,0,-w);
}
ZKW();
printf("%d %d\n",mxflow,mncost);
return 0;
}
例题:
首先计算出所有仓库货物总量的平均值即每个仓库的目标状态。对于每个仓库,若它目前的储量大于该值,则由\(s\)向它连一条边,否则就由它向\(t\)连一条边,容量即为|该仓库目前的流量 - 平均值|,费用为0 ; 对于每个仓库,由它向它相邻的两个仓库连边,容量为\(inf\),费用为1;跑最小费用最大流即可。
int main()
{
n = read(); s = 0;t = n + 1;
for(int i = 1;i <= n;i ++)
{
b[i] = read();
sum += b[i];
}
sum /= n;
for(int i = 1;i <= n;i ++) b[i] -= sum;
for(int i = 1;i <= n;i ++)
{
if(b[i] > 0){add(s,i,b[i],0);add(i,s,0,0);}//
if(b[i] < 0){add(i,t,-b[i],0);add(t,i,0,0);}//
}
for(int i = 1;i <= n;i ++)
{
if(i != 1){add(i,i - 1,inf,1);add(i - 1,i,0,-1);}
if(i != n){add(i,i + 1,inf,1);add(i + 1,i,0,-1);}
}
add(1,n,inf,1);add(n,1,0,-1);
add(n,1,inf,1);add(1,n,0,-1);
mcmf();
printf("%d\n",mncost);
return 0;
}
对于这道题,我们惊奇的发现油箱里还有多少油很重要,因为当油量为0时我们必须加油,而且还必须保证油量递减,所以考虑拆点分层。我们将每个点拆成\(k + 1\)个点,第一个点表示油量为\(k\),第二个点表示油量为\(k - 1\)······第\(k + 1\)个点表示没有油啦。
考虑如何建边呢?
1、对于有加油站的点,观察题目中性质3,我们必须加满油,所以我们可以从该点的第\(2 - k + 1\)层均向第一层连边,表示无论如何的都要加满油,费用为\(A\),容量为1,当然也只有第一层才会向下一个点连边,容量为1,费用依据\(x、y\)是否减小来判断即可。
2.对于没有加油站的点,我们从该点的第\(i\)层\((i \in [1,k])\)向下一个点的第\(i + 1\)层连边,表示油量减少了一,容量均为1,费用分开考虑即可,但是对于第\(k + 1\)层的点,已经没有油了,所以我们必须给汽车加油,所以我们应该向下一个点的第二层(走过去的过程中回消耗一单位流量)连一条容量为1,费用为\(A + C\)的边,当然还要考虑\(B\)的贡献啦。
建完边之后,跑最小费用最大流即可。
int main()
{
n = read();k = read();A = read();b = read();c = read();
s = 0;t = n * n * (k + 1) + 1;
add(s,id(1,1,1),1,0); add(id(1,1,1),s,0,0);
for(int i = 1;i <= k + 1;i ++)
{
add(id(n,n,i),t,1,0);
add(t,id(n,n,i),0,0);
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= n;j ++)
{
int xx,yy,x = read();
if(x == 1)
{
for(int w = 2;w <= k + 1;w ++)
{
add(id(i,j,w),id(i,j,1),1,A);
add(id(i,j,1),id(i,j,w),0,-A);
}
for(int w = 1;w <= 4;w ++)
{
xx = i + dx[w];yy = j + dy[w];
if(xx < 1 || xx > n || yy < 1 || yy > n) continue;
if(dx[w] == -1 || dy[w] == -1)
{
add(id(i,j,1),id(xx,yy,2),1,b);
add(id(xx,yy,2),id(i,j,1),0,-b);
}
else
{
add(id(i,j,1),id(xx,yy,2),1,0);
add(id(xx,yy,2),id(i,j,1),0,0);
}
}
}
else
{
for(int w = 1;w <= k;w ++)
{
for(int l = 1;l <= 4;l ++)
{
xx = i + dx[l];yy = j + dy[l];
if(xx < 1 || xx > n || yy < 1 || yy > n) continue;
if(dx[l] == -1 || dy[l] == -1)
{
add(id(i,j,w),id(xx,yy,w + 1),1,b);
add(id(xx,yy,w + 1),id(i,j,w),0,-b);
}
else
{
add(id(i,j,w),id(xx,yy,w + 1),1,0);
add(id(xx,yy,w + 1),id(i,j,w),0,0);
}
}
}
for(int w = 1;w <= 4;w ++)
{
xx = i + dx[w],yy = j + dy[w];
if(xx < 1 || xx > n || yy < 1 || yy > n) continue;
if(dx[w] == -1 || dy[w] == -1)
{
add(id(i,j,k + 1),id(xx,yy,2),1,A + c + b);
add(id(xx,yy,2),id(i,j,k + 1),0,-(A + b + c));
}
else
{
add(id(i,j,k + 1),id(xx,yy,2),1,A + c);
add(id(xx,yy,2),id(i,j,k + 1),0,-(A + c));
}
}
}
}
printf("%d\n",MCMF());
return 0;
}
我们从每一个点\(i\)向它的下一个点\(i + 1\)连一条容量为\(inf\)的边,然后从源点向第一个点连一条容量为\(k\)的边,代表每个点最多被覆盖\(k\)次,从最后一个点向汇点也连一条容量为\(k\)的边。对于每一个区间,我们从区间的左端点\(l\)向其右端点\(r\)连边肯定是少不了的啦,那么考虑,如何把我们最终的目标即统计所有合法区间的长度与它联系起来呢?我们可以想到除了容量再来一个费用来统计答案,那么费用大小是什么呢?当然是区间长度啦。接下来再考虑,我们想让线段长度总和最大,所以我们可以对所有费用取反,然后跑一次最小费用最大流,最后再对跑出来的最小费用取反就是答案啦。至于我们刚开始连的那些边,费用显然为0,因为他们并没有贡献。
由于并没有给出坐标范围,所以我们可以稍稍离散化一下。
int main()
{
n = read();k = read();
for(int i = 1;i <= n;i ++)
{
l[i] = read();r[i] = read();
if(l[i] > r[i]) swap(l[i],r[i]);
b[(i << 1) - 1] = l[i];
b[i << 1] = r[i];
}
sort(b + 1,b + 2 * n + 1);
int len = unique(b + 1,b + 2 * n + 1) - b - 1;
s = 0;t = len + 1;
for(int i = 1;i <= n;i ++)
{
int L = lower_bound(b,b + len + 1,l[i]) - b;
int R = lower_bound(b,b + len + 1,r[i]) - b;
add(L,R,1,l[i] - r[i]); add(R,L,0,r[i] - l[i]);
}
add(s,1,k,0); add(1,s,0,0);
add(len,t,k,0); add(t,len,0,0);
for(int i = 1;i < len;i ++){add(i,i + 1,inf,0);add(i + 1,i,0,0);}
MCMF();
printf("%d\n",-mncost);
return 0;
}
这道题和上一道题谜之相似有木有。。但观察这两道题的区别,上一道题是区间,而这道题是线段,那么想一想区间和线段有什么区别呢?显然区间一定不会垂直于x轴,而线段会。。但是对于垂直于x轴的情况,若我们仍然直接向上一道题一样连边,我们会发现出现了负边权的自环,那么对于\(spfa\),它死循环了。。。
所以我们想到了拆点,将每个点\(x\)拆成点\(2 * x\)和\(2 * x + 1\),并将这两个点之间的那条边看做是原先的点\(x\),那么对于左右端点(我们将线段上较小的横坐标看做左端点,将线段上较大的横坐标看做右端点)相同的情况,我们令左端点是\(2 * x\),右端点是\(2 * x + 1\),表示会覆盖\(x\)这个点,对于左右端点不同的情况,我们令左端点为\(2 * l + 1\),右端点为\(2 * r\),表示会覆盖\([l + 1,r - 1]\)(开线段),然后我们发现这样建边极其的有道理,而且\(the\) \(most\) \(important\)它过了。。。
int main()
{
n = read();k = read();
for(int i = 1;i <= n;i ++)
{
l[i] = read();x[i] = read();r[i] = read();y[i] = read();
length[i] = sqrt((long long)(l[i] - r[i]) * (l[i] - r[i]) + (long long)(x[i] - y[i]) * (x[i] - y[i]));
if(l[i] > r[i]) swap(l[i],r[i]);
l[i] <<= 1;r[i] <<= 1;
if(l[i] == r[i]) r[i] ++; else l[i] ++;
b[(i << 1) - 1] = l[i];
b[i << 1] = r[i];
}
sort(b + 1,b + 2 * n + 1);
int len = unique(b + 1,b + 2 * n + 1) - b - 1;
s = 0;t = len + 1;
for(int i = 1;i <= n;i ++)
{
int L = lower_bound(b,b + len + 1,l[i]) - b;
int R = lower_bound(b,b + len + 1,r[i]) - b;
add(L,R,1,-length[i]); add(R,L,0,length[i]);
}
add(s,1,k,0); add(1,s,0,0);
add(len,t,k,0); add(t,len,0,0);
for(int i = 1;i < len;i ++){add(i,i + 1,inf,0);add(i + 1,i,0,0);}
MCMF();
printf("%d\n",-mncost);
return 0;
}
当然,你也可以这样:
int main()
{
n = read();k = read();
for(int i = 1;i <= n;i ++)
{
l[i] = read();x[i] = read();r[i] = read();y[i] = read();
if(l[i] > r[i]) swap(l[i],r[i]);
b[(i << 1) - 1] = l[i];
b[i << 1] = r[i];
length[i] = sqrt((long long)(l[i] - r[i]) * (l[i] - r[i]) + (long long)(x[i] - y[i]) * (x[i] - y[i]));
}
sort(b + 1,b + 2 * n + 1);
int len = unique(b + 1,b + 2 * n + 1) - b - 1;
s = 0;t = len * 2 + 1;
for(int i = 1;i <= n;i ++)
{
int L = lower_bound(b,b + len + 1,l[i]) - b;
int R = lower_bound(b,b + len + 1,r[i]) - b;
if(L == R)
{
add(L << 1,L << 1 | 1,1,-length[i]);
add(L << 1 | 1,L << 1,0,length[i]);
continue;
}
add(L << 1 | 1,R << 1,1,-length[i]); add(R << 1,L << 1 | 1,0,length[i]);
}
add(s,1,k,0); add(1,s,0,0);
add(len * 2,t,k,0); add(t,len * 2,0,0);
for(int i = 1;i < 2 * len;i ++){add(i,i + 1,inf,0);add(i + 1,i,0,0);}
MCMF();
printf("%d\n",-mncost);
return 0;
}
由于每天开始的时候只有干净的毛巾可用,每天结束的时候只有脏毛巾需要操作,因此我们考虑拆点,将每个点\(i\)拆成早上\(i\)和晚上\(i+N\)两个点。接下来考虑建边。
设该天需要\(x\)条干净毛巾,那么为了限制我们使用的是\(x\)条干净毛巾,我们从\(i\)向汇点连一条容量为\(x\),费用为0的边。而对于这\(x\)条干净毛巾的来源:(1)可以是直接购买,因此从源点向\(i\)连一条容量为\(inf\),费用为\(p\)的边;(2)也可以是之前快洗或慢洗到期了(我们一会考虑该天脏毛巾的去处时再讨论该情况)。
那么对于脏毛巾呢?首先,为了限制我们产生了\(x\)条脏毛巾,我们从源点向\(i+N\)连一条容量为\(x\),费用为0的边。那么脏毛巾的去处呢?(1)可以继承到下一天的脏毛巾中,因为到最后有的毛巾完全可以不洗,所以不一定要送到快洗店或慢洗店,我们从\(i+N\)向\(i+1+N\)连一条容量为\(inf\),费用为0的边;(2)送到快洗店,所以我们从\(i+N\) 向\(i+m\)连一条容量为\(inf\),费用为\(f\)的边;(3)送到慢洗店,所以我们从\(i+N\) 向\(i+n\)连一条容量为\(inf\),费用为\(s\)的边。
然后跑费用流。
友情提示:
1.希望你不要见祖宗。。。
2.想在\(loj\)上双倍经验的小盆友请务必仔细观察\(loj\)的输入格式。。。
int main()
{
n = read();
s = 0;t = 2 * n + 1;
for(int i = 1,x;i <= n;i ++)
{
x = read();
add(s,i + n,x,0); add(i + n,s,0,0);
add(i,t,x,0); add(t,i,0,0);
}
nc = read(); fd = read(); fc = read(); sd = read(); sc = read();
for(int i = 1;i <= n;i ++)
{
if(i + 1 <= n) {add(i + n,i + 1 + n,inf,0);add(i + 1 + n,i + n,0,0);}
if(i + sd <= n) {add(i + n,i + sd,inf,sc);add(i + sd,i + n,0,-sc);}
if(i + fd <= n) {add(i + n,i + fd,inf,fc);add(i + fd,i + n,0,-fc);}
add(s,i,inf,nc);add(i,s,0,-nc);
}
printf("%lld\n",MCMF());
return 0;
}
这道题嘛。。。首先是个最大费用(满足要求的最佳航空路线)最大流(两条航线的限制),最大费用可以用每条边的费用取反后求得的最小费用取反得到。
首先每个点都限制只能经过一次,所以我们很自然地想到拆点,于是我们将每个点\(i\)拆成\(i\)和\(i+n\),并从\(i\)向\(i+n\)连一条容量为1,费用为-1的边(若经过这个点,那么它会产生贡献),特殊的,城市\(1\)和城市\(n\)的容量为2。
若\(x\)和\(y\)之间有一条边(强制令\(x<y\)),那么我们从\(x+n\)向\(y\)连一条容量为\(inf\)(反正点上有限流),费用为0的边(城市之间不会产生贡献)。
从源点向城市1连一条容量为2,费用为0的边,从城市\(n\)向汇点连一条容量为2,费用为0的边。
输出方案时\(dfs\)求解即可,但是判断细节还是有的,详见代码:
void get_ans(int x)
{
v[x] = 1;
ans[++ cnt] = x;
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(v[y]) continue;
if(a[i].val != a[i].begin) get_ans(y);
}
}
int main()
{
n = read();m = read();
s = 0; t = 2 * n + 1;
add(s,1,2,0); add(1,s,0,0);
add(2 * n,t,2,0); add(t,2 * n,0,0);
add(1,1 + n,2,-1); add(1 + n,1,0,1);
add(n,2 * n,2,-1); add(n,2 * n,0,1);
for(int i = 2;i < n;i ++) {add(i,i + n,1,-1);add(i + n,i,0,1);}
for(int i = 1;i <= n;i ++)
{
cin >> em[i];
dy[em[i]] = i;
}
for(int i = 1;i <= m;i ++)
{
cin >> s1 >> s2;
int x = dy[s1],y = dy[s2];
if(x == 1 && y == n) is = 1;
if(x > y) swap(x,y);
add(x + n,y,inf,0); add(y,x + n,0,0);
//注意这里其实容量必须是inf而不能是1,否则对于只有城市1和城市n的情况,本来是有解的,会误判成无解
}
MCMF();
if(mxflow < 2) {printf("No Solution!\n");return 0;}
printf("%d\n",- mncost - 2);
get_ans(1);
for(int i = 1;i <= cnt;i ++) if(ans[i] <= n && ans[i] >= 1) cout << em[ans[i]] << endl;
cout << em[1] << endl;
return 0;
}
首先声明,这道题动态规划是错的,所以,乖乖写网络流吧(づ。◕ᴗᴗ◕。)づ
对于这道题,显然是最大费用(岩石标本数量最多)最大流(探测车的数量最多)。
考虑怎么建边,首先有的地方有价值,有的地方没有价值,所以可以想到拆点,并用拆出的两点之间的边的费用来表示是否有价值,拆出的两点之间的容量为\(inf\)代表一个点可以经过多次。那么对于点与点之间呢?我们枚举每个点\((x,y)\)(不能是障碍)下面和右面的那两个点,如果既未出界而且还不是障碍,那就由\(id(x,y)+p*q\)向那个点(\(id(x+1,y)\)或\(id(x,y+1)\))连一条容量为\(inf\),费用为0的边就好啦。最后,不要忘记源点向点\((1,1)\)连一条容量为\(n\),费用为0的边,以及从\(id(p,q)+p*q\)向汇点连一条容量为\(n\),费用为0的边来限流哦。
void dfs(int x,int y,int pos,int now)
{
for(int i = head[pos];i;i = a[i].nex)
{
int v = a[i].to,em;
if(v == s || v == t || v == pos - p * q || !a[i ^ 1].val) continue;
a[i ^ 1].val --;
//千万不要忘了
if(v == pos + p * q){dfs(x,y,v,now);return;}
//只会在pos==1的时候出现该情况,但是不判断是不对滴!
if(v == id(x,y) + 1) {em = 1;y ++;}
else {em = 0;x ++;}
printf("%d %d\n",now,em);
dfs(x,y,v + p * q,now);
return;
}
}
int main()
{
n = read();p = read();q = read();
swap(p,q);
s = 0;t = 2 * p * q + 1;
for(int i = 1;i <= p;i ++)
for(int j = 1;j <= q;j ++)
{
is[i][j] = read();
if(is[i][j] == 1) continue;
int now = id(i,j);
add(now,now + p * q,inf,0); add(now + p * q,now,0,0);
if(is[i][j] == 2) {add(now,now + p * q,1,1);add(now + p * q,now,0,-1);}
}
if(is[1][1] != 1) {add(s,id(1,1),n,0);add(id(1,1),s,0,0);}
if(is[p][q] != 1) {add(id(p,q) + p * q,t,n,0);add(t,id(p,q) + p * q,0,0);}
for(int i = 1;i <= p;i ++)
for(int j = 1;j <= q;j ++)
{
if(is[i][j] == 1) continue;
if(is[i][j + 1] != 1 && j + 1 <= q) {add(id(i,j) + p * q,id(i,j + 1),inf,0);add(id(i,j + 1),id(i,j) + p * q,0,0);}
if(is[i + 1][j] != 1 && i + 1 <= p) {add(id(i,j) + p * q,id(i + 1,j),inf,0);add(id(i + 1,j),id(i,j) + p * q,0,0);}
}
MCMF();
for(int i = 1;i <= mxflow;i ++) dfs(1,1,1,i);
return 0;
}
建两列点,左边一列与源点相连表示人,右边一列与汇点相连表示工作,从源点向人连一条容量为1,费用为0的边,从工作向汇点连一条容量为1,费用为0的边。
从人向工作连一条容量为1,费用为该人做该工作的效益的边。
然后,显然,跑一遍最小费用最大流,再跑一遍最大费用最大流就好啦。
int main()
{
n = read();
s = 0;t = 2 * n + 1;
for(int i = 1;i <= n;i ++)
{
add1(s,i,1,0); add1(n + i,t,1,0);
add2(s,i,1,0); add2(n + i,t,1,0);
}
int x;
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= n;j ++)
{
x = read();
add1(i,j + n,1,x);
add2(i,j + n,1,x);
}
printf("%d\n",MNCMF());
printf("%d\n",MXCMF());
return 0;
}
和上一道题一毛一样系不系?
只需要把从源点到仓库的容量改为\(a_{i}\),把从零售商店到汇点的容量改为\(b_{i}\)就好啦。
int main()
{
m = read();n = read();
s = 0;t = m + n + 1;
for(int i = 1,x;i <= m;i ++)
{
x = read();
add1(s,i,x,0); add2(s,i,x,0);
}
for(int i = 1,x;i <= n;i ++)
{
x = read();
add1(i + m,t,x,0); add2(i + m,t,x,0);
}
int x;
for(int i = 1;i <= m;i ++)
for(int j = 1;j <= n;j ++)
{
x = read();
add1(i,j + m,inf,x);
add2(i,j + m,inf,x);
}
printf("%d\n",MNCMF());
printf("%d\n",MXCMF());
return 0;
}
这道题,显然最大费用最大流。。
我们从源点向每个起点连一条容量为\(k\),费用为0的边来限制机器人数目;同理,从每个终点向汇点连一条容量为\(r\),费用为0的边。至于点与点之间的连边,首先为了保证图的连通性,从每个点向它的上面和右面连一条容量为\(inf\),费用为0的边,然后考虑到有的移动是有价值的,所以我们对于有价值的移动再在两点之间连一条容量为1,费用为\(x\)的边。
int main()
{
A = read();B = read();n = read();m = read();
n ++; m ++;
s = 0;t = n * m + 1;
for(int i = 1,x;i <= n;i ++)
for(int j = 1;j < m;j ++)
{
x = read();
add(id(i,j),id(i,j + 1),1,x); add(id(i,j + 1),id(i,j),0,-x);
add(id(i,j),id(i,j + 1),inf,0); add(id(i,j + 1),id(i,j),0,0);
}
for(int j = 1,x;j <= m;j ++)
for(int i = 1;i < n;i ++)
{
x = read();
add(id(i,j),id(i + 1,j),1,x); add(id(i + 1,j),id(i,j),0,-x);
add(id(i,j),id(i + 1,j),inf,0); add(id(i + 1,j),id(i,j),0,0);
}
for(int i = 1,k,x,y;i <= A;i ++)
{
k = read();x = read();y = read();
add(s,id(x + 1,y + 1),k,0); add(id(x + 1,y + 1),s,0,0);
}
for(int i = 1,k,x,y;i <= B;i ++)
{
k = read();x = read();y = read();
add(id(x + 1,y + 1),t,k,0); add(t,id(x + 1,y + 1),0,0);
}
printf("%d\n",MCMF());
return 0;
}
不知道为啥,这年头网络流24题,费用流那么多。。。(自打费用流入库以来,就独得24题恩宠,费用流呀,告诉24题,要雨露均沾,可它,偏偏是不听呢╮(─▽─)╭)
这道题,首先由问题一考虑拆点,我们将每个点\(i\)拆成\(i\)和\(i+(2*m+n-1)*n/2\),然后搞一搞就好了。
1.每个点拆成的两个点之间容量为1,费用为该点数字;每个点向它左下和右下的点连边,容量为1,费用为0;由源点向第一行的\(m\)个点连边,容量为1,费用为0(必须从\(m\)个点各出发一次);由第\(n\)行的每个点向汇点连边,容量为1,费用为0;
2.在第一问的基础上,将每个点拆成的两个点之间的容量改成\(inf\),将第\(n\)行的点向汇点连的边的容量改成\(inf\)(可以在同一个点结束);
3.在第二问的基础上,将每个点向它左下和右下连的边的容量改成\(inf\);
int main()
{
m = read();n = read();
s = 0;t = (2 * m + n - 1) * n + 1;
for(int i = 1,x,now = m;i <= n;i ++,now ++)
for(int j = 1;j <= now;j ++)
{
x = read();
num[i][j] = ++ cnt;
add1(num[i][j],num[i][j] + (2 * m + n - 1) * n / 2,1,x);
add2(num[i][j],num[i][j] + (2 * m + n - 1) * n / 2,inf,x);
add3(num[i][j],num[i][j] + (2 * m + n - 1) * n / 2,inf,x);
}
for(int i = 1;i <= m;i ++)
{
add1(s,num[1][i],1,0);
add2(s,num[1][i],1,0);
add3(s,num[1][i],1,0);
}
for(int i = 1,now = m;i < n;i ++,now ++)
for(int j = 1;j <= now;j ++)
{
add1(num[i][j] + (2 * m + n - 1) * n / 2,num[i + 1][j],1,0);
add1(num[i][j] + (2 * m + n - 1) * n / 2,num[i + 1][j + 1],1,0);
add2(num[i][j] + (2 * m + n - 1) * n / 2,num[i + 1][j],1,0);
add2(num[i][j] + (2 * m + n - 1) * n / 2,num[i + 1][j + 1],1,0);
add3(num[i][j] + (2 * m + n - 1) * n / 2,num[i + 1][j],inf,0);
add3(num[i][j] + (2 * m + n - 1) * n / 2,num[i + 1][j + 1],inf,0);
}
for(int j = 1;j <= m + n - 1;j ++)
{
add1(num[n][j] + (2 * m + n - 1) * n / 2,t,1,0);
add2(num[n][j] + (2 * m + n - 1) * n / 2,t,inf,0);
add3(num[n][j] + (2 * m + n - 1) * n / 2,t,inf,0);
//注意这里是inf,因为可以在同一点结束,但是s连边时不可以在同一点开始
}
printf("%d\n",MCMF1());
printf("%d\n",MCMF2());
printf("%d\n",MCMF3());
return 0;
}
最小割
割
对于一个网络流图\(G = (V,E)\),其割的定义为一种点的划分方式:将所有的点划分为\(S\)和\(T = V - S\)两个集合,其中源点\(s \in S\),汇点\(t \in T\)。
割的容量
我们的定义割\((S,T)\)的容量\(c(S,T)\)表示所有从\(S\)到\(T\)的边的容量之和,即\(c(S,T) = \sum_{u\in S,v\in T}c(u,v)\),当然我们也可以用\(c(s,t)\)表示\(c(S,T)\)。
最小割
最小割就是求得一个割\((S,T)\)使得割的容量\(c(S,T)\)最小。
最大流最小割定理
\(f(s,t)_{max} = c(s,t)_{min}\)(最大流\(=\)最小割)
证明
我们来想一个问题,我们求得最大流时一条路径的最大流受限于什么呢?当然是这条路径上的最小流量对不对,那么我们现在要求最小割,即花费最小的代价使得从源点到汇点 没有一条路径联通,那么我们割去哪条边呢?当然也是这条路径上的边权最小的边啦,所以,是不是一样呢?~~
例题:
emm,对于这道题,首先它不可能是最大流。其次也不会是费用流,然后我们想,它是不是最小割呢?我们发现实验的收益和仪器的费用总要花出去一个的,也就是说他们不共存,然后我们惊奇的最小割发现好像很对的样子。。
根据最大流最小割定理,我们想要求除最小割,求出最大流就好啦。(来一遍\(Dinic\),解决你的烦恼。)。
那么考虑怎么建边,从源点向实验连一条容量为该实验费用的边,从每个实验向它对应的仪器连一条容量为\(inf\)的边(为了使这条边不会被割去),最后从每个仪器向汇点连一条容量为该仪器费用的边。而我们最终的最大收益就是所有实验的收益之和 - 最小割(最大流)。
最后输出方案时,我们发现若一条边被割掉(也就是说没有选择它)的话,那么这条边在跑完最大流后一定流满了,那么它的剩余流量就会变成0,所以它一定不会出现在残量网络中,也就是说\(d[\)该点\(] = 0\),所以小力判断一下就好了。
int main()
{
m = read();n = read();
s = 0;t = m + n + 1;
for(int i = 1,x;i <= m;i ++)
{
scanf("%d",&x); sum += x;
add(s,i,x); add(i,s,0);
memset(tools,0,sizeof(tools));
cin.getline(tools,10000);
int ulen = 0,tool;
while (sscanf(tools + ulen,"%d",&tool) == 1)
{
add(i,m + tool,inf); add(m + tool,i,0);
if(tool == 0) ulen ++;
else while(tool){tool /= 10;ulen ++;}
ulen ++;
}
}
for(int i = 1,x;i <= n;i ++)
{
x = read();
add(m + i,t,x); add(t,m + i,0);
}
int em = Dinic();
for(int i = 1;i <= m;i ++)
if(d[i]) ans[++ cnt] = i;
for(int i = 1;i <= cnt;i ++)
if(i != cnt) printf("%d ",ans[i]);
else printf("%d",ans[i]);
printf("\n");
cnt = 0;
for(int i = 1;i <= n;i ++)
if(d[i + m]) ans[++ cnt] = i;
for(int i = 1;i <= cnt;i ++)
if(i != cnt) printf("%d ",ans[i]);
else printf("%d",ans[i]);
printf("\n");
printf("%d\n",sum - em);
return 0;
}
由于这道题说任意两个数没有公共边,显然这是一个黑白点(根据横纵坐标和的奇偶性来分)不能共存的问题,不能共存,于是我们想一想最小割,那么对于这道题怎么建边呢?
由于是黑白点(暂且规定黑点的横纵坐标和为奇数,白点的为偶数)不能共存,我们可以令源点向黑点连一条容量为该点权值的边,令白点向汇点连一条容量为该点权值的边,并令每个黑点向它四周的白点(注意判断不要出界)连一条容量为\(inf\)的边表示不能共存,那么跑一边最小割后就会把不能共存的点对中权值较小的点“割去”,所以最后我们想要求的最大权值和就是总的权值和 - 最大流。
int main()
{
n = read();m = read();
s = 0;t = n * m + 1;
int x;
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
x = read(); sum += x;
if((i + j) & 1)
{
add(s,id(i,j),x); add(id(i,j),s,0);
for(int k = 1;k <= 4;k ++)
{
int xx = i + dx[k],yy = j + dy[k];
if(xx < 1 || xx > n || yy < 1 || yy > m) continue;
add(id(i,j),id(xx,yy),inf); add(id(xx,yy),id(i,j),0);
}
}
else{add(id(i,j),t,x); add(t,id(i,j),0);}
}
printf("%d\n",sum - Dinic());
return 0;
}
对于这道题,我们观察到部分黑白点是不能共存的,所以我们仿照上一道题的思路,从源点向黑点连一条容量为1的边,从白点向汇点连一条容量为1的边,那么中间部分怎么连边呢?显然,我们只需要让不能共存的点之间连边就好啦,我们可以枚举每个黑点可以攻击到的8个格子,若出界或者有障碍则跳过,否则在他们之间连一条容量为\(inf\)的边,然后求最小割(也就是跑一遍最大流啦)得到的结果就是我们必须舍弃的点,所以最后答案就是合法点 - 最大流,即 \(n*n-m-mxflow\)。
int main()
{
n = read();m = read();
s = 0; t = n * n + 1;
for(int i = 1,x,y;i <= m;i ++)
{
x = read();y = read();
is[x][y] = 1;
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= n;j ++)
{
if(is[i][j]) continue;
if((i + j) & 1)
{
add(s,id(i,j),1); add(id(i,j),s,0);
for(int k = 1;k <= 8;k ++)
{
int x = i + dx[k],y = j + dy[k];
if(x < 1 || x > n || y < 1 || y > n || is[x][y]) continue;
add(id(i,j),id(x,y),inf); add(id(x,y),id(i,j),0);
}
}
else{add(id(i,j),t,1);add(t,id(i,j),0);}
}
printf("%d\n",n * n - m - Dinic());
return 0;
}
有那么两道题
它们明明是状压+\(bfs\) 、状压+最短路
可是它们却混进了网络流24题(起码以我的能力以及我搜罗到的题解并没有发现网络流解法。。)
它们的名字叫“孤岛营救问题”(p4011)和“软件补丁”(p2761)
咱们就不讲了哈。。
更多方法期待你们去开拓哦。所以要不也留成习题好了啦٩(๑❛ᴗ❛๑)۶哈哈~
上下界
无源汇有上下界可行流
问题描述:
给你一张\(n\)个点\(m\)条边的有向图,没有源点和汇点,每条边有一个最低流量和最高流量,问在满足流量平衡(各个节点不储水,流入等于流出)的前提下,能否满足所有的流量限制?
由于强制要求流量下界,因此可以先把下界减去,将每条边的容量改为流量上界减去流量下界,即默认已经流了与下界相等的流,但问题是,在此情况下,可能导致流量不平衡,也就是说,可能存在点的总流入大于总流出,也可能存在点的总流出大于总流入,肿么办捏?
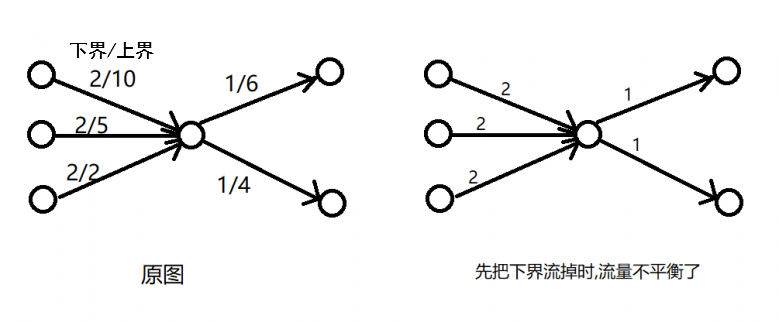
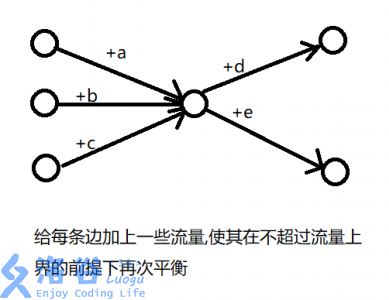
那么考虑肿么实现捏,我们可以新建一个超级源点和一个超级汇点,对于总流入大于总流出的边,我们从源点向他连一条流量为总流入\(-\)总流出的边;对于总流出大于总流入的边,我们从他向汇点连一条流量为总流出\(-\)总流入的边,然后在新图上跑一遍最大流,若跑出来达到了满流,则可行,否则不可行,考虑为啥捏,大家应该都知道吧。。。
那么新问题来了,我们如何快速得知是否满流呢,一个直观朴素的方法便是扫描每一条与源点相连的边,判断是否均没有剩余流量,若是,则满流,反则反之。不过我们在这里使用一种更简便的方法,用数组\(du[i]\)表示点\(i\)的总流入\(-\)总流出,记\(sum = \displaystyle\sum_{i}^{du[i] > 0}du[i]\),若最大流\(=sum\),说明满流,否则不满。
板子:loj115
int main()
{
n = read();m = read();
s = 0;t = n + 1;
for(int i = 1,x,y,r;i <= m;i ++)
{
x = read();y = read();l[i] = read();r = read();
add(x,y,r - l[i]); add(y,x,0);
du[x] -= l[i]; du[y] += l[i];
c[i] = tot;
}
for(int i = 1;i <= n;i ++)
{
if(du[i] > 0)
{
add(s,i,du[i]); add(i,s,0);
sum += du[i];
}
else if(du[i] != 0){add(i,t,-du[i]);add(t,i,0);}
}
int flow;
while(bfs()) while(flow = dfs(s,inf)) mxflow += flow;
if(mxflow != sum){printf("NO\n");return 0;}
printf("YES\n");
for(int i = 1;i <= m;i ++) printf("%d\n",l[i] + a[c[i]].val);
return 0;
}
这里其实有一道题,但是那道题和板子一毛毛一样,就是多组数据而已,有兴趣的同学请拜访ZOJ2314 Reactor Cooling
良心讲课者在此提醒您,切题千万法,细心第一法,多组不清空,爆零两行泪/(ㄒoㄒ)/
有源汇有上下界可行流
其实和无源汇时一样,但是无源汇时,所有点的流入流量都等于其流出流量,但对于本题,有两个例外:源点和汇点,因此可以连一条\(t\)到\(s\),下界为\(0\),上界为\(inf\)的边,这样有源汇的问题就解决啦。
由于并没有找到板子,直接上题吧。
1.把每一行看做一个点, 把每一列看做一个点。
2.建立一个源点s,连接s与每一行,容量上限下限设为该行和。(因为是强制限定的)
3.建立一个汇点t,连接每一列与t,容量上限下限设为该列和。
4.我们用从行向列的边表示一个点,那么我们从每个点的对应的行向它对应的列连一条流量范围为\([down[i][j],up[i][j]]\)的边。
5.建边\((t,s,inf)\)。
6.跑无源汇有上下界可行流判断是否可行。
void init()
{
memset(head,0,sizeof(head));
memset(up,0x3f,sizeof(up));
memset(down,0,sizeof(down));
memset(du,0,sizeof(du));
tot = 1; t = n + m + 1;
sum = mxflow = s = flag = 0;
ss = n + m + 2; tt = n + m + 3;
}
int main()
{
T = read();
while(T -- > 0)
{
n = read();m = read(); init();
for(int i = 1,x;i <= n;i ++)
{
x = read();
add(s,i,0); add(i,s,0);
du[s] -= x; du[i] += x;
}
for(int i = 1,x;i <= m;i ++)
{
x = read();
add(n + i,t,0); add(t,n + i,0);
du[n + i] -= x; du[t] += x;
}
c = read(); int x,y,z;
while(c -- > 0)
{
x = read(); y = read(); scanf("%s",em); z = read();
if(x == 0 && y)
{
for(int i = 1;i <= n;i ++)
{
if(em[0] == '=')
{
if(up[i][y] < z || down[i][y] > z) flag = 1;
up[i][y] = down[i][y] = z;
}
else if(em[0] == '<') up[i][y] = min(up[i][y],z - 1);
else if(em[0] == '>') down[i][y] = max(down[i][y],z + 1);
}
}
else if(x && y == 0)
{
for(int i = 1;i <= m;i ++)
{
if(em[0] == '=')
{
if(up[x][i] < z || down[x][i] > z) flag = 1;
up[x][i] = down[x][i] = z;
}
else if(em[0] == '<') up[x][i] = min(up[x][i],z - 1);
else if(em[0] == '>') down[x][i] = max(down[x][i],z + 1);
}
}
else if(x == 0 && y == 0)
{
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
if(em[0] == '=')
{
if(up[i][j] < z || down[i][j] > z) flag = 1;
up[i][j] = down[i][j] = z;
}
else if(em[0] == '<') up[i][j] = min(up[i][j],z - 1);
else if(em[0] == '>') down[i][j] = max(down[i][j],z + 1);
}
}
else
{
if(em[0] == '=')
{
if(up[x][y] < z || down[x][y] > z) flag = 1;
up[x][y] = down[x][y] = z;
}
else if(em[0] == '<') up[x][y] = min(up[x][y],z - 1);
else if(em[0] == '>') down[x][y] = max(down[x][y],z + 1);
}
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
if(up[i][j] < down[i][j]) flag = 1;
add(i,n + j,up[i][j] - down[i][j]);
add(n + j,i,0); e[i][j] = tot;
du[i] -= down[i][j];
du[j + n] += down[i][j];
}
if(flag){printf("IMPOSSIBLE\n");continue;}
add(t,s,inf); add(s,t,0);
for(int i = 0;i <= t;i ++)
{
if(du[i] > 0)
{
add(ss,i,du[i]); add(i,ss,0);
sum += du[i];
}
else if(du[i] != 0){add(i,tt,- du[i]);add(tt,i,0);}
}
int flow;
while(bfs()) while(flow = dfs(ss,inf)) mxflow += flow;
if(mxflow != sum){printf("IMPOSSIBLE\n");continue;}
for(int i = 1;i <= n;i ++,printf("\n"))
for(int j = 1;j <= m;j ++,printf(" "))
printf("%d",a[e[i][j]].val + down[i][j]);
}
return 0;
}
有源汇有上下界最大流
我们考虑,按照有源汇有上下界可行流跑一遍出来的最大流,是否是我们想要的答案?
答案显然是否定的。。。
为啥么捏?因为刚开始将下界流完的时候,有的点本身就是平衡的,因此你并未令他们在新图中连边,然而可能有的点虽然已经平衡,但是他们所连的边上是有残量的,因此我们会错误的忽视这些点,导致少算一部分流量。
那么怎么解决这个问题呢?我们可以从\(ss\)到\(tt\)跑完一遍最大流并取\(s\)到\(t\)路径上的流量后,在残量网络中从\(s\)到\(t\)再跑一遍最大流,意思也就是,在已经满足流量平衡的条件下,尽可能的再多流些流量。
第一次跑最大流后,从\(s\)到\(t\)的流量即为从\(t\)到\(s\)那条边上流过的的流量(第一次跑完最大流即意味着此时图上的所有点已满足流量平衡(由无源汇有上下界可行流那套理论可知),那么从\(s\)到\(t\)的流量肯定等于从\(t\)到\(s\)连的那条边上流过的流量),那也就等于从\(t\)到\(s\)那条边的反向边上的流量即一条从\(s\)到的\(t\)的边上的流量,那么第二次在残量网络上跑出的从\(s\)到\(t\)的最大流是肯定会加上这一部分流量,然而这一部分流量是并不存在于原图中的,那么如果再加一次就会多加,因此只需要加一次就好啦,那么我们最终的答案其实就是在刚开始”改建“的图上从\(ss\)到\(tt\)跑一遍最大流后,再在残量网络上从\(s\)到\(t\)跑出的最大流。
板子:loj116
int main()
{
n = read();m = read();s = read();t = read();
ss = 0;tt = n + 1;
for(int i = 1,x,y,l,r;i <= m;i ++)
{
x = read();y = read();l = read();r = read();
add(x,y,r - l); add(y,x,0);
du[x] -= l; du[y] += l;
}
for(int i = 1;i <= n;i ++)
{
if(du[i] > 0)
{
add(ss,i,du[i]); add(i,ss,0);
sum += du[i];
}
else if(du[i] != 0){add(i,tt,-du[i]);add(tt,i,0);}
}
add(t,s,inf); add(s,t,0);
int flow;
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
if(mxflow != sum){printf("please go home to sleep\n");return 0;}
mxflow = 0;
while(bfs(s,t)) while(flow = dfs(s,inf,t)) mxflow += flow;
printf("%d\n",mxflow);
return 0;
}
这道题很显然的样子有木有捏?我们只需要从源点向每一天连一条容量为\(d_i\)的边,从每一个女孩向汇点连一条流量范围为\([g_i,inf]\)的边,由每一天向该天对应的女孩连一条流量范围为\([l_i,r_i]\)的边就好了。。然后就是套模板了。。。
void init()
{
tot = 1; sum = mxflow = 0;
for(int i = 0;i <= n + m + 5;i ++) head[i] = du[i] = 0;
vec.clear();
}
int main()
{
while(scanf("%d%d",&n,&m) != EOF)
{
init();
s = 0;t = n + m + 1;
ss = n + m + 2;tt = n + m + 3;
for(int i = 1,x;i <= m;i ++)
{
x = read();
add(n + i,t,inf - x); add(t,n + i,0);
du[n + i] -= x; du[t] += x;
}
for(int i = 1,c,d;i <= n;i ++)
{
c = read();d = read();
add(s,i,d); add(i,s,0);
while(c -- > 0)
{
int T,l,r;
T = read();l = read();r = read();
T ++;
add(i,n + T,r - l); add(n + T,i,0);
du[i] -= l; du[n + T] += l;
vec.push_back(make_pair(tot,l));
}
}
for(int i = 0;i <= n + m + 1;i ++)
{
if(du[i] > 0)
{
add(ss,i,du[i]); add(i,ss,0);
sum += du[i];
}
else if(du[i] != 0){add(i,tt,-du[i]);add(tt,i,0);}
}
add(t,s,inf); add(s,t,0);
int flow;
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
if(mxflow != sum){printf("-1\n");puts("");continue;}
mxflow = 0;
while(bfs(s,t)) while(flow = dfs(s,inf,t)) mxflow += flow;
printf("%d\n",mxflow);
for(int i = 0;i < (int)vec.size();i ++) printf("%d\n",a[vec[i].first].val + vec[i].second);
puts("");
}
return 0;
}
有源汇有上下界最小流
这个问题有两种解法。
解一:
仿照上面的思路,先从\(t\)到\(s\)连一条容量为\(inf\)的边,然后从\(ss\)到\(tt\)跑最大流。然而这样可能会多算一部分流,那么怎么减去呢?我们可以在残量网络上再从\(t\)到\(s\)跑一边最大流,并将其减去(显然这样仍满足流量平衡),注意,第二次求从\(t\)到\(s\)的最大流时,一定要把从\(t\)到\(s\)的那条容量为\(inf\)的边去掉。
int main()
{
n = read();m = read();s = read();t = read();
ss = 0;tt = n + 1;
for(int i = 1,x,y,l,r;i <= m;i ++)
{
x = read();y = read();l = read();r = read();
add(x,y,r - l); add(y,x,0);
du[x] -= l; du[y] += l;
}
for(int i = 1;i <= n;i ++)
{
if(du[i] > 0)
{
add(ss,i,du[i]); add(i,ss,0);
sum += du[i];
}
else if(du[i] != 0){add(i,tt,-du[i]);add(tt,i,0);}
}
add(t,s,inf); add(s,t,0);
int flow;
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
if(mxflow != sum){printf("please go home to sleep\n");return 0;}
mxflow = a[tot].val;
head[t] = a[head[t]].nex; head[s] = a[head[s]].nex;
while(bfs(t,s)) while(flow = dfs(t,inf,s)) mxflow -= flow;
printf("%d\n",mxflow);
return 0;
}
解二:
我们先不建\((t - > s,inf)\)这条边,直接从\(ss\)到\(tt\)跑一遍最大流。然后从\(t\)向\(s\)连一条容量为\(inf\)的边,再跑一次最大流,最后答案就是\(inf\)这条边上流过的流量。
我们考虑为什么直接连上这条边跑出来的可行流不是最小流呢?
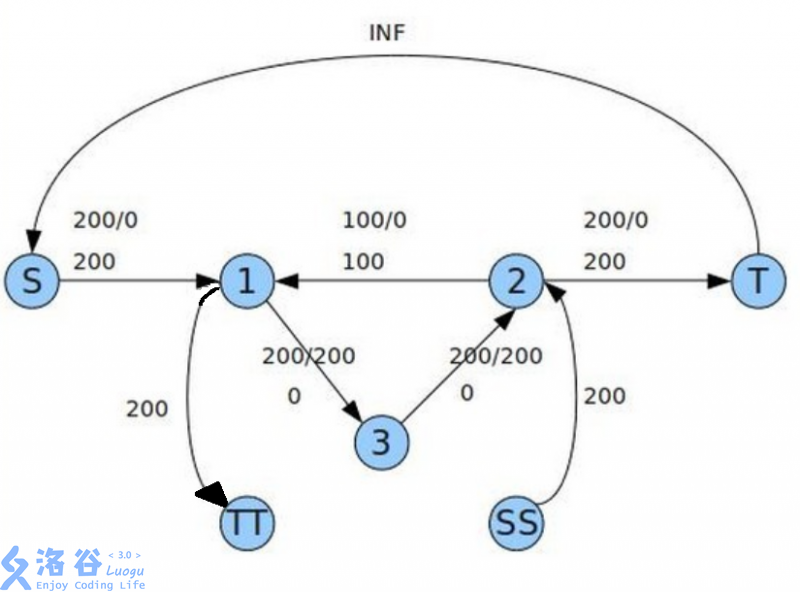
对于上图,若直接跑,求得的最小流是200,而实际上可行最小流是100.
为啥么捏?原因是图中存在环(循环流),而我们并没有利用,导致流增大。
那我们现在开始先不连\(t\)到\(s\)的边,直接跑一遍,就先把这些不影响源汇点的循环流尽可能地流掉了,这样第二次连上\(t\)到\(s\)时流的流就一定是最小可行流了。
int main()
{
n = read();m = read();s = read();t = read();
ss = 0;tt = n + 1;
for(int i = 1,x,y,l,r;i <= m;i ++)
{
x = read();y = read();l = read();r = read();
add(x,y,r - l); add(y,x,0);
du[x] -= l; du[y] += l;
}
for(int i = 1;i <= n;i ++)
{
if(du[i] > 0)
{
add(ss,i,du[i]); add(i,ss,0);
sum += du[i];
}
else if(du[i] != 0){add(i,tt,-du[i]);add(tt,i,0);}
}
int flow;
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
add(t,s,inf); add(s,t,0);
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
if(mxflow != sum){printf("please go home to sleep\n");return 0;}
printf("%d\n",a[tot].val);
return 0;
}
板子:loj117
由于本人快菜成一团了,因此这道题只拿了95分,死活TLE一个点。。但是方法保证正确,希望各位做过之后来援助我一下。。。
从\(s\)向每个点连一条容量为\(inf\)的边,表示可以从总部传送人到该点\(inf\)次;
从每个点向比它低的点连一条边,流量下界为\(1\),表示该雪道最少清理\(1\)次,流量上界为\(inf\),表示该雪道最多清理\(inf\)次;
从每个点向汇点连一条容量为\(inf\)的边,表示可以在任意一个点向总部传回人\(inf\)次。
然后你惊奇的发现这好像是有源汇有上下界最小流。所以,套板子就好啦~~
int main()
{
n = read();
s = 0;t = n + 1;
ss = n + 2;tt = n + 3;
for(int i = 1,x,y;i <= n;i ++)
{
x = read();
for(int j = 1;j <= x;j ++)
{
y = read();
add(i,y,inf - 1); add(y,i,0);
du[i] --; du[y] ++;
}
}
for(int i = 1;i <= n;i ++)
{
add(s,i,inf); add(i,s,0);
add(i,t,inf); add(t,i,0);
}
for(int i = 0;i <= n + 1;i ++)
{
if(du[i] > 0)
{
sum += du[i];
add(ss,i,du[i]); add(i,ss,0);
}
else if(du[i] != 0){add(i,tt,-du[i]);add(tt,i,0);}
}
int flow;
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
add(t,s,inf); add(s,t,0);
while(bfs(ss,tt)) while(flow = dfs(ss,inf,tt)) mxflow += flow;
if(mxflow != sum){printf("please go home to sleep\n");return 0;}
printf("%d\n",a[tot].val);
return 0;
}
最小割树
最小割树的定义:
定义一棵树T为最小割树,需要满足对于树上的所有边\((s,t)\),树上去掉\((s,t)\)后产生的两个集合恰好是原图上\((s,t)\)的最小割把原图分成的两个集合,且边\((s,t)\)的权值等于原图上\((s,t)\)的最小割 。
最小割树的构造:
定义中说:树上去掉\((s,t)\)后产生的两个集合恰好是原图上\((s,t)\)的最小割把原图分成的两个集合。
所以我们递归构造最小割树。
在当前的点集中随意选取两个点\(s,t\),在原图中跑出它们之间的最小割,然后在树上连一条\((s,t,\lambda(s,t))\)的无向边,然后找出\(s,t\)所属的两个点集,并对其进行递归操作,当点集中只剩一个点的时候停止。
最小割树的查询:
最小割树满足一个很重要的性质:原图上\(u,v\)两点的最小割就是最小割树上\(u\)到\(v\)路径上权值最小的边。
因此我们可以直接倍增就好了。
证明:
我们设\(\lambda(a,b)\)表示\(a,b\)的最小割的权值。
引理1.对于任意\(p\in V_x,q\in V_y\),有\(\lambda(x,y)>=\lambda(p,q)\)。
假设\(\lambda(x,y)<\lambda(p,q)\),那么用割断\((x,y)\)的代价割不断\((p,q)\),但是\(p\)与\(x\)联通,\(q\)与\(y\)联通,那么\((x,y)\)也不会被割断,与最小割定义矛盾,所以1.得证。
定理1.对于任意不同的三点\(a,b,c\),\(\lambda(a,b)>=min(\lambda(a,c),\lambda(b,c))\)。
设\(\lambda(a,b),\lambda(a,c),\lambda(b,c)\)中最小的是\(\lambda(a,b)\),删掉\((a,b)\)之后\(c\)与\(b\)联通。
由引理1.可得\(\lambda(a,c)<=\lambda(a,b)\),又因为之前的假设,因此\(\lambda(a,b)=\lambda(a,c)\)
因此这三者中一定有两个较小值,一个较大值
若 \(\lambda(a,b)\) 是小的,则\(\lambda(a,c),\lambda(b,c)\)中一个较大的,一个较小的,取min之后还是较小值,定理显然成立
若\(\lambda(a,b)\)是大的,则\(\lambda(a,c),\lambda(b,c)\)都是较小值,定理显然成立
3.定理1的推论:
对于任意不同的两点\(u,v\), \(\lambda(u,v)>=min(\lambda(u,w_1),\lambda(w_1,w_2),\lambda(w_2,w_3)...,\lambda(w_k,v))\)。
4.定理2: 对于任意不同的两点\(x,y\),令\(p,q\)为最小割树\(x\)到\(y\)路径上的两点,且\(\lambda(p,q)\)最小,那么\(\lambda(x,y)=\lambda(p,q)\),也就是说,\(u,v\)两点最小割就是最小割树上\(u\)到\(v\)的路径上权值最小的边。
由定理1的推论可知$\lambda(x,y)>=\lambda(p,q) $
又根据最小割树的定义,\(x,y\)在\(p,q\)最小割的两侧,则\(\lambda(p,q)>=\lambda(x,y)\)
因此\(\lambda(x,y)=\lambda(p,q)\)
#include<iostream>
#include<cstdio>
#include<queue>
#include<cmath>
#include<cstring>
#define R register
using namespace std;
const int N = 505;
const int inf = 0x3f3f3f3f;
queue<int> q;
int n,m,tot = 1,head[N],Q,cnt,head1[N],f[N][10],em[N],d[N],tmp1[N],tmp2[N],mn[N][10];
struct node{int to,nex,val;}a[6005],b[3005];
inline int read()
{
R int x = 0,f = 1; R char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 3) + (x << 1) + (ch ^ 48);ch = getchar();}
return x * f;
}
void add(int x,int y,int z)
{
a[++ tot].to = y;
a[tot].val = z;
a[tot].nex = head[x];
head[x] = tot;
}
void add_tree(int x,int y,int z)
{
b[++ cnt].to = y;
b[cnt].val = z;
b[cnt].nex = head1[x];
head1[x] = cnt;
}
void init()
{
for(R int i = 2;i <= tot;i += 2)
{
a[i].val = a[i].val + a[i ^ 1].val;
a[i ^ 1].val = 0;
}
}
bool bfs(int s,int t)
{
while(!q.empty()) q.pop();
for(R int i = 0;i <= n;i ++) d[i] = 0;
d[s] = 1; q.push(s);
while(!q.empty())
{
R int x = q.front(); q.pop();
for(R int i = head[x];i;i = a[i].nex)
{
R int y = a[i].to;
if(!d[y] && a[i].val)
{
d[y] = d[x] + 1;
if(y == t) return 1;
q.push(y);
}
}
}
return 0;
}
int dfs(int x,int want,int t)
{
if(x == t || !want) return want;
R int f = 0,get = 0;
for(R int i = head[x];i && want;i = a[i].nex)
{
R int y = a[i].to;
if(d[y] == d[x] + 1 && a[i].val)
{
f = dfs(y,min(a[i].val,want),t);
if(!y)
{
d[y] = 0;
continue;
}
a[i].val -= f; a[i ^ 1].val += f;
want -= f; get += f;
}
}
return get;
}
int dinic(int s,int t)
{
init();
R int mxflow = 0,flow;
while(bfs(s,t)) while(flow = dfs(s,inf,t)) mxflow += flow;
return mxflow;
}
void build(int l,int r)
{
if(l == r) return;
R int s = em[l],t = em[r];
R int value = dinic(s,t);
add_tree(s,t,value); add_tree(t,s,value);
R int cnt1 = 0,cnt2 = 0;
for(R int i = l;i <= r;i ++)
{
if(d[em[i]]) tmp1[++ cnt1] = em[i];
else tmp2[++ cnt2] = em[i];
}
for(R int i = 1;i <= cnt1;i ++) em[l + i - 1] = tmp1[i];
for(R int i = 1;i <= cnt2;i ++) em[l + cnt1 + i - 1] = tmp2[i];
build(l,l + cnt1 - 1);
build(l + cnt1,r);
}
void get(int x,int fa)
{
d[x] = d[fa] + 1;
for(R int i = 1;i <= 9;i ++)
{
f[x][i] = f[f[x][i - 1]][i - 1];
mn[x][i] = min(mn[f[x][i - 1]][i - 1],mn[x][i - 1]);
}
for(R int i = head1[x];i;i = b[i].nex)
{
R int y = b[i].to;
if(y == fa) continue;
f[y][0] = x; mn[y][0] = b[i].val;
get(y,x);
}
}
void work()
{
for(R int i = 1;i <= n;i ++) em[i] = i;
build(1,n);
memset(mn,0x3f,sizeof(mn));
get(1,0);
}
int query(int x,int y)
{
R int res = inf;
if(d[x] < d[y]) swap(x,y);
for(R int i = 9;i >= 0;i --)
if((d[x] - d[y]) & (1 << i))
{
res = min(res,mn[x][i]);
x = f[x][i];
}
if(x == y) return res;
for(R int i = 9;i >= 0;i --)
if(f[x][i] != f[y][i])
{
res = min(res,mn[x][i]); res = min(res,mn[y][i]);
x = f[x][i]; y = f[y][i];
}
res = min(res,mn[x][0]); res = min(res,mn[y][0]);
return res;
}
int main()
{
n = read();m = read();
for(R int i = 1,x,y,z;i <= m;i ++)
{
x = read();y = read();z = read();
add(x,y,z); add(y,x,0);
add(y,x,z); add(x,y,0);
}
work();
Q = read();
for(R int i = 1,x,y;i <= Q;i ++)
{
x = read();y = read();
R int ans = query(x,y);
printf("%d\n",ans == inf ? -1 : ans);
}
return 0;
}
(⊙o⊙)…,和模板一样的有没有。。
就是统计一下就好了,可以用一下\(set\)什么之类的。。
int main()
{
n = read();m = read();
for(R int i = 1,x,y,z;i <= m;i ++)
{
x = read();y = read();z = read();
add(x,y,z); add(y,x,0);
add(y,x,z); add(x,y,0);
}
work();
for(int i = 1;i <= n;i ++)
for(int j = i + 1;j <= n;j ++)
s.insert(query(i,j));
printf("%d\n",s.size());
return 0;
}
surprise
既然讲完了板子和网络流24题,接下来,我们告别标签,来一轮紧张刺激的例题怎么样?
对于这道题嘛,首先它是一个最小割。

因为我们发现如果一个同学他选了文科,那么不管是他自己选理科的贡献,还是他和周围同学一起选理科的贡献都是得不到的,也就是说,他们不共存。所以我们可以往最小割方面想一想。
接下来我们考虑怎么建边呢?
我们首先从源点向每一个点连一条容量为该点选文科所得贡献的边,同理,我们从每个点向汇点连一条容量为该点选理科所得贡献的边。然后考虑每个同学和他周围的同学一块选文科或理科的贡献,以文科为例,我们新建一个节点,并从源点向新节点连一条容量为他们一起选文科所得贡献的边,然后再从这个点向这两个同学连一条容量为\(inf\)的边就好啦,这样的话他们一起选文科所得贡献就一定不会和他们有人选理科所得贡献冲突了。选理科同理。。
int main()
{
n = read();m = read();
s = 0;t = n * m * 5 + 1;
int x,now;
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
x = read(); sum += x;
add(s,id(i,j),x); add(id(i,j),s,0);
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
x = read(); sum += x;
add(id(i,j),t,x); add(t,id(i,j),0);
}
for(int i = 1;i <= n - 1;i ++)
for(int j = 1;j <= m;j ++)
{
x = read(); cnt ++;
now = n * m + cnt; sum += x;
add(s,now,x); add(now,s,0);
add(now,id(i,j),inf); add(id(i,j),now,0);
add(now,id(i + 1,j),inf); add(id(i + 1,j),now,0);
}
for(int i = 1;i <= n - 1;i ++)
for(int j = 1;j <= m;j ++)
{
x = read(); cnt ++;
now = n * m + cnt; sum += x;
add(now,t,x); add(t,now,0);
add(id(i,j),now,inf); add(now,id(i,j),0);
add(id(i + 1,j),now,inf); add(now,id(i + 1,j),0);
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m - 1;j ++)
{
x = read(); cnt ++;
now = n * m + cnt; sum += x;
add(s,now,x); add(now,s,0);
add(now,id(i,j),inf); add(id(i,j),now,0);
add(now,id(i,j + 1),inf); add(id(i,j + 1),now,0);
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m - 1;j ++)
{
x = read(); cnt ++;
now = n * m + cnt; sum += x;
add(now,t,x); add(t,now,0);
add(id(i,j),now,inf); add(now,id(i,j),0);
add(id(i,j + 1),now,inf); add(now,id(i,j + 1),0);
}
printf("%d\n",sum - Dinic());
return 0;
}
不知道大家有没有想到一个双倍经验的题,它叫文理分科,在这里就不讲啦,但是可以以后练题的时候做了哦p4313文理分科
仔细读一遍题意,你发现这是一个最小割问题,可是对于这道题我们好像需要割点,怎么办呢?
将割点转化成割边不就好了吗。。。
所以我们就开始拆点啦,将每个点\(i\)拆成\(i\)和\(i+n\),并连一条容量为该点控制费用的边。
对于高速公路呢?假设这条边是\((x,y)\),我们就从\(x+n\)向\(y\)以及从\(y+n\)向\(x\)连一条容量为\(inf\)的边就行了啦(反正不能割),注意是双向边哦。
然后跑一遍最大流就好啦。
那么输出方案呢?
我们从\(s\)开始\(dfs\)并给递归到的点打上标记,若该边剩余流量大于0,则递归下去,最后枚举每一条边\((x,y)\),如果你发现\(x\)被打了标记而\(y\)没有,那你就输出\(x\)就好啦(因为这条边一定是从某个\(i\)指向\(i+n\)的,所以输出\(x\))。
void dfs(int x)
{
v[x] = 1;
for(int i = head[x];i;i = a[i].nex)
{
int y = a[i].to;
if(a[i].val && !v[y]) dfs(y);
}
}
int main()
{
n = read();m = read();s = read();t = read();
for(int i = 1,x;i <= n;i ++)
{
x = read();
add(i,i + n,x); add(i + n,i,0);
}
for(int i = 1,x,y;i <= m;i ++)
{
x = read();y = read();
add(x + n,y,inf); add(y,x + n,0);
add(y + n,x,inf); add(x,y + n,0);
}
Dinic(s,n + t); dfs(s);
for(int i = 2;i <= tot;i += 2) if(v[a[i].from] && !v[a[i].to]) printf("%d ",a[i].from);
return 0;
}
首先介绍一个概念,闭合子图:对于每个点,从它出发,能够走到的点都属于闭合子图中。
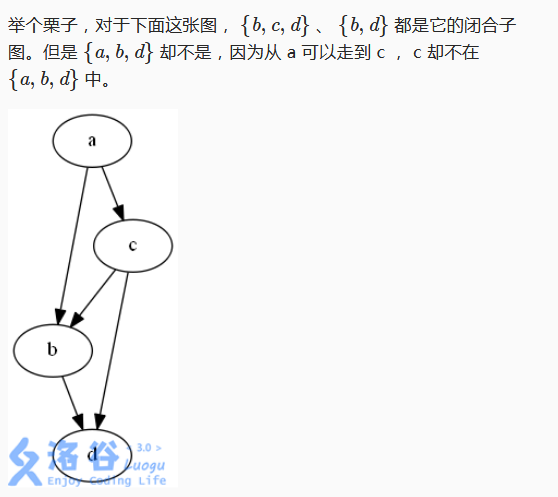
另一个概念,最大权闭合子图:原图中点权和最大的闭合子图。
最大权闭合子图问题可以用最小割解决~~
连边方式:
1.对于所有原图中的边\((u,v)\),连边\(u->v\),容量为\(inf\)。
2.对于每个原图中的点\(i\),设它的权值为\(val[i]\):若\(val[i]>0\),则从\(s\)向\(i\)连边,容量为\(val[i]\);若\(val[i]<0\),则从\(i\)向\(t\)连边,容量为\(-val[i]\);若\(val[i]=0\),无论与\(s\)还是\(t\)连边均可。
再次来自某谷的一个例图:(右图是原图,左图是用来求解网络流的建好的图)
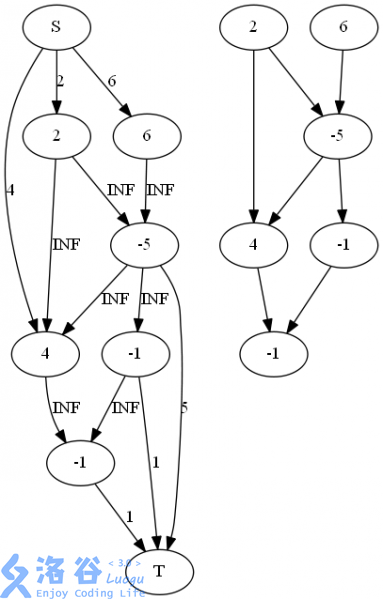
直接跑最小割即可,那么最大权 = 正点权和 - 最小割,最大权闭合子图的节点就是最后与\(s\)联通的部分。
为什么这样是正确的呢?
首先,我们从\(s\)到\(t\)的路径上一定会经过一些正边权的边,同样也会经过一些负边权的边,考虑我们会割去哪些边呢?当然是绝对值小的边啦,所以我们小力讨论一下:若负边权和的绝对值小,那么我们会减去这些负边权,而我们刚开始统计的是正点权和,所以我们直接减就好啦,所以合法;若正边权和的绝对值小,那么我们会舍弃这些正边权但也不会减去负边权,所以也是直接减就好啦,再次合法。。(完美؏؏☝ᖗ乛◡乛ᖘ☝؏؏)
前置知识暂且到此为止~~
我们观察这道题,本题有一个隐含条件:如果你要攻击植物\(i\),那么你就必须把\(i\)的右边的植物以及保护它的植物都吃掉
所以我们的建图方式:
1.植物\(i\)的点权为\(val[i]\),如何与源点和汇点连边见上文;
2.所有植物\(i\)向它的右边连边;
3.如果一个植物\(j\)保护\(i\),则由\(i\)向\(j\)连边;
这样的话若想得到\(i\)的收益,那么它之前的植物的收益即使是负的也一定会被减去,否则若得到\(i\)的收益不优的话,就不会攻击\(i\)以及它前面的植物。
but(由英语老师的教导可知,下面是重点)
如果成环了呢?
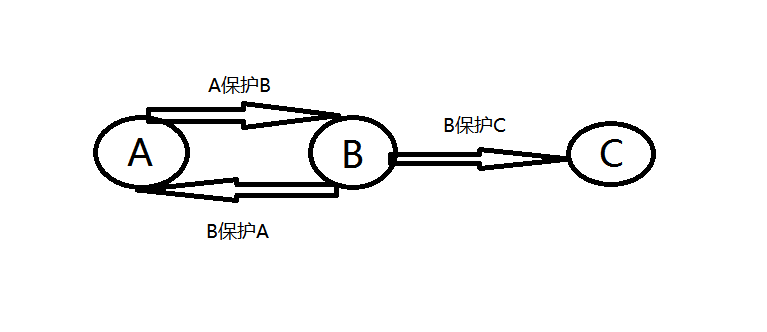
你发现如果两个植物相互保护,僵尸无论如何都攻击不到他们,而被环保护的植物也不会被攻击到。
所以我们应该将环中的点以及被环保护的点去掉,所以我们可以建关于网络流的图的反向图(若\(i\)保护\(j\),则由\(i\)向\(j\)连一条边)并进行拓扑,能够被拓扑排序遍历到的节点才能被用来建图。
void topsort()
{
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
if(!in[id(i,j)]) q.push(id(i,j));
while(!q.empty())
{
int x = q.front(); q.pop(); v[x] = 1;
for(int i = 1;i <= out[x][0];i ++)
{
int y = out[x][i];
in[y] --;
if(in[y] == 0) q.push(y);
}
}
}
int main()
{
n = read();m = read();
for(int i = 1;i <= n;i ++)
{
for(int j = 1;j <= m;j ++)
{
int cnt,x,y,now = id(i,j);
val[now] = read();cnt = read();
for(int k = 1;k <= cnt;k ++)
{
x = read();y = read();
x ++; y ++;
out[now][++ out[now][0]] = id(x,y);
in[id(x,y)] ++;
}
if(j != m)
{
out[id(i,j + 1)][++ out[id(i,j + 1)][0]] = now;
in[now] ++;
}
}
}
topsort();
s = 0;t = n * m + 1;
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
{
int now = id(i,j);
if(!v[now]) continue;
if(val[now] > 0)
{
add(s,now,val[now]); add(now,s,0);
sum += val[now];
}
else{add(now,t,-val[now]);add(t,now,0);}
for(int k = 1;k <= out[now][0];k ++)
{
int y = out[now][k];
if(v[y]) {add(y,now,inf);add(now,y,0);}
}
}
printf("%d\n",sum - Dinic());
return 0;
}
说个实话,有没有发现这三道题都是最小割?其实这是我看最小割的题少得可怜所以用来补补坑的。。。
✿✿ヽ(゚▽゚)ノ✿完结撒花!





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 解答了困扰我五年的技术问题
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· DeepSeek 解答了困扰我五年的技术问题。时代确实变了!
· PPT革命!DeepSeek+Kimi=N小时工作5分钟完成?
· What?废柴, 还在本地部署DeepSeek吗?Are you kidding?
· DeepSeek企业级部署实战指南:从服务器选型到Dify私有化落地
· 程序员转型AI:行业分析