CF1630A And Matching 题解

题目描述

有 \(n\) 个数 \(0,1,2,\cdots,n-1\)。你需要把他们两两分组，使得每组两个数按位与的结果之和 \(=k\)。如果可能，请构造出一组可能的 \(\frac n2\) 个数对，否则输出 -1。

保证 \(n\) 是 \(2\) 的幂，\(k\le n-1\)

思路

首先我们发现，\(n\) 是二的幂，所以按照二进制的角度看，这些数字从 \(\texttt{000...000}\) 到 \(\texttt{111...111}\) 全部都有。

我们分三种情况讨论：

• \(k=0\)：对于这种情况，我们把每一个数字和它取反后的结果与起来：

  以二进制的角度看，就是：\((000\&111)=0,(001\&110)=0,(010\&101)=0,(011\&100)=0\)

• \(1\le k \le n-2\)：这种情况比较复杂，我们考虑使得其中一组答案为 \(k\)，其他均为 \(0\)，不难发现我们可以把 \(k\) 和 \(n-1\) 分为一组，由于 \(n=2^x\)，因此 \(n-1\) 二进制位全部为 \(1\)，所以这一组答案 \(=k\)，然后剩下的按照取反分组（\(k\) 取反的结果和 \(0\)（\(n-1\) 取反的结果）分组）。

• \(k=n-1\)：

  • \(n=2 或4\)：暴力证明无解

  • \(n>4\)：我们来模拟一下 \(n=8\) 的情况：

    

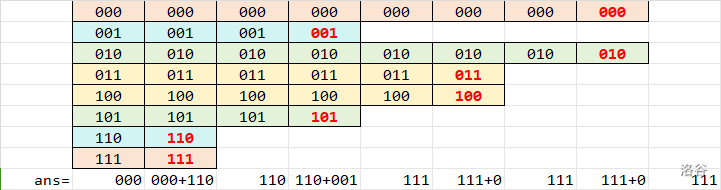
    概括就是：

    我们称一个数为另一个数的“反数”，当且仅当这两个数每个二进制位上的数都相反。

    我们称一个数为“孤立的数”，当且仅当这个数的反数已经和别的数组成一对。

    • 首先配对 \((n-2,n-1)\)，结果为 \(\texttt{111...110}\)，孤立的数：\(0(n-1的反数),1(n-2的反数)\)
    • 然后配对 \((n-3,1)\)，结果为 \(\texttt{000...001}\)，孤立的数：\(0,2(n-3的反数)\)​
    • 此时 \(ans=n-1\)。
    • 最后把所有数和其反数配对，结果均为 \(0\)，再把两个孤立的数 \(0,2\) 配对，结果也为 \(0\)。

代码

#include <bits/stdc++.h>
using namespace std;

int n,k;
void Main()
{
    scanf("%d%d",&n,&k);
    if(k==0){
        for(int i=0;i<n/2;i++){
            printf("%d %d\n",i,(n-1)-i);
        }
    }else if(k<n-1){
        printf("%d %d\n",0,(n-1)-k);
        printf("%d %d\n",k,n-1);
        for(int i=1;i<n/2;i++){
            if(i!=k and (n-1)-i!=k) printf("%d %d\n",i,(n-1)-i);
        }
    }else{
        if(n<=4){
            puts("-1");
        }else{
            printf("%d %d\n",0,2);
            printf("%d %d\n",1,n-3);
            printf("%d %d\n",n-2,n-1);
            for(int i=3;i<n/2;i++){
                if(i!=k and (n-1)-i!=k) printf("%d %d\n",i,(n-1)-i);
            }
        }
    }
}

int T;
int main()
{
    scanf("%d",&T);
    while(T--){
        Main();
    }
    return 0;
}