谢老师2024春 - Day1:组合数学
Day1:组合数学
A - P5520 [yLOI2019] 青原樱
隔板法:
- 已选择的位置:\(m\) 棵樱花树。
- 未选择的位置:\(n-m\) 个空位置
- 板的数量(一棵樱花树就是一个板):\(m\) 个板子
- 板子可以放在两边,得:\(\tbinom{n-m+1}{m}m!\)
\(\tbinom{n-m+1}{m}m!=\frac{A_{n-m+1}^{m}}{m!}m!=A_{n-m+1}^{m}\)
完事。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int T,n,m,p;
int A(int n,int m,int p){
int res=1,x=n;
for(int i=1;i<=m;i++){
res=(res*x)%p,x--;
}return res;
}
signed main()
{
scanf("%lld%lld%lld%lld",&T,&n,&m,&p);
printf("%lld",A(n-m+1,m,p));
return 0;
}
B - P1313 [NOIP2011 提高组] 计算系数
板子,直接杨辉三角即可,注意需要先把 \(a,b\) 取模一下。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod=10007;
int C[1005][1005];
int a,b,k,n,m;
int Fast_power(int base,int power){
int res=1%mod;
while(power){
if(power&1) res=(res*base)%mod;
base=(base*base)%mod;
power>>=1;
}
return res;
}
void Calc_C(int k){
for(int i=0;i<=k;i++){
for(int j=0;j<=i;j++){
if(j==0 or j==i) C[i][j]=1;
else C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
}
}
signed main()
{
scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);a%=mod;b%=mod;
int ans=(Fast_power(a,n)*Fast_power(b,m))%mod;
Calc_C(k);ans=(ans*C[k][n])%mod;
printf("%lld",ans);
return 0;
}
C - P3197 [HNOI2008] 越狱
越狱的情况 \(=\) 所有情况 \(-\) 不越狱的情况。
- 所有情况直接幂
- 不越狱的情况,\(A\) 随便选 \(m\) 种,\(B\) 只能选择与 \(A\) 不同的 \(m-1\) 种,\(C\) 只能选与 \(B\) 不同的 \(m-1\) 种 \(\cdots\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=100003;
int m,n;
int Fast_power(int base,int power){
int res=1;
while(power){
if(power&1) res=(res*base)%mod;
base=(base*base)%mod;
power>>=1;
}return res;
}
signed main()
{
scanf("%lld%lld",&m,&n);
int All=Fast_power(m,n);
int Cant=(m*Fast_power(m-1,n-1))%mod;
printf("%lld",(mod+All-Cant)%mod);
return 0;
}
D - P2822 [NOIP2016 提高组] 组合数问题
因为每组数据 \(k\) 一定,所以杨辉三角 \(+\) 二维前缀和。
#include <bits/stdc++.h>
using namespace std;
int C[2005][2005],sum[2005][2005];
int T,k,n,m;
void Calc_C(){
for(int i=0;i<=2000;i++){
for(int j=0;j<=i;j++){
if(j==0 or j==i) C[i][j]=1;
else C[i][j]=(C[i-1][j-1]+C[i-1][j])%k;
}
}
for(int i=1;i<=2000;i++){
for(int j=1;j<=i;j++){
sum[i][j]=(C[i][j]==0)+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}sum[i][i+1]=sum[i][i];
}
}
int main()
{
scanf("%d%d",&T,&k);Calc_C();
while(T--){
scanf("%d%d",&n,&m);
printf("%d\n",sum[n][min(n,m)]);
}
return 0;
}
E - P2532 [AHOI2012] 树屋阶梯
考虑递推:\(dp_i\) 表示高度为 \(i\) 的阶梯用 \(i\) 个钢材的搭建方案数。
比如我们以 \(dp_4\) 为例。

注意需要高精度,此处不放高精度模板了,想要完整的板子戳这里
#include <bits/stdc++.h>
using namespace std;
//Some BigInt Code
Bint dp[505];
int N;
int main()
{
scanf("%d",&N);dp[0]=dp[1]=1;
for(int i=2;i<=N;i++){
for(int l1=0,l2=i-1;l1<=i-1;l1++,l2--){
dp[i]+=dp[l1]*dp[l2];
}
}
cout<<dp[N];
return 0;
}
F - P2290 [HNOI2004] 树的计数
不会。
G - P3807 【模板】卢卡斯定理/Lucas 定理
板子。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int Inverse[100005];
int frac[100005];
int T,n,m,p;
int FastPower(int base,int power,int mod){
int res=1%mod;
while(power){
if(power&1) res=1ll*res*base%mod;
power>>=1;
base=1ll*(base*base)%mod;
}return res;
}
void Init(int p){
memset(frac,0,sizeof(frac));frac[0]=1;
for(int i=1;i<=p;i++) frac[i]=(1ll*frac[i-1]*i)%p;
for(int i=1;i<=p;i++) Inverse[i]=FastPower(i,p-2,p);
}
int MiniC(int n,int m){
if(n<m) return 0;
else return (1ll*frac[n]*Inverse[frac[m]]*Inverse[frac[n-m]])%p;
}
int C(int n,int m,int p){
if(n<p and m<p) return MiniC(n,m)%p;
else return (1ll*C(n/p,m/p,p)*MiniC(n%p,m%p))%p;
}
signed main()
{
scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&m,&p);Init(p);
printf("%d\n",C(m+n,n,p));
}
return 0;
}
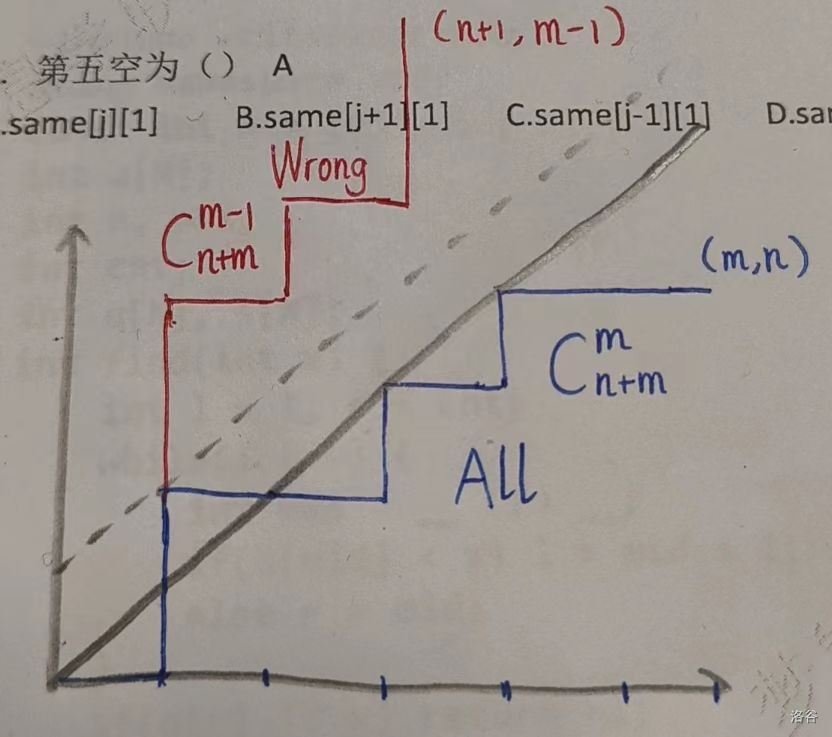
H - P1641 [SCOI2010] 生成字符串
魔改卡特兰数,Lucas 套一套就好了:
#include <bits/stdc++.h>
using namespace std;
int fact[20100405];
int n,m,p;
int FastPower(int base,int power,int mod){
int res=1;
while(power){
if(power&1) res=1ll*res*base%mod;
base=(1ll*base*base)%mod;
power>>=1;
}return res;
}
void Init(){
memset(fact,0,sizeof(fact));fact[0]=1;
for(int i=1;i<=n+m;i++) fact[i]=(1ll*fact[i-1]*i)%p;
}
int C(int n,int m){
int res=1;
res=(1ll*res*fact[n])%p;
res=(1ll*res*FastPower(fact[n-m],p-2,p))%p;
res=(1ll*res*FastPower(fact[m],p-2,p))%p;
return res;
}
signed main()
{
scanf("%d%d",&n,&m);p=20100403;Init();
printf("%d\n",(p+C(n+m,m)-C(m+n,m-1))%p);
return 0;
}
P2480 [SDOI2010] 古代猪文
不会。
P3726 [AH2017/HNOI2017] 抛硬币
不会。


