CF1857G Counting Graphs 题解

题目描述#

给定一棵最小生成树，求有多少张图的最小生成树是给定的树，并且这张图的所有边边权不超过 \(S\)。

思路#

考虑在最小生成树中加边。

我们回顾一下 Kruskal 的过程：

1. 找到没被用过的，最小的边
2. 判断这条边的两端是否在一个联通块中
3. 加入这条边，将两端的联通块连在一起

根据第三条，我们可以得出一个结论：只要在加边时，保证加入的边是给定的边，这张图的最小生成树就一定是给定的树。

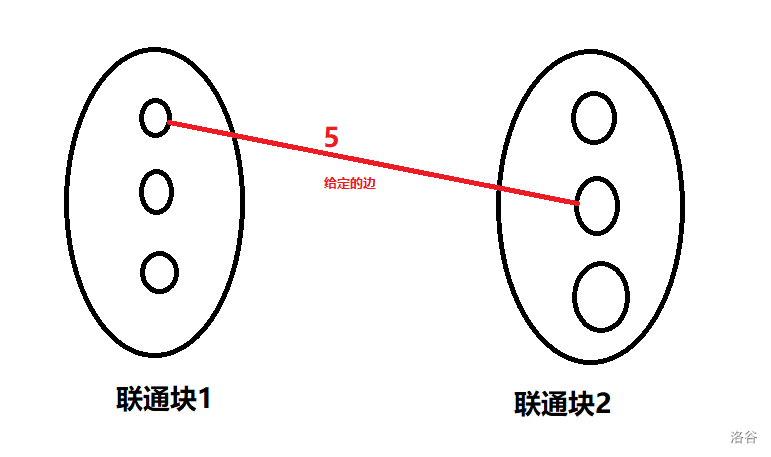
因此，在这两个联通块之间加任意一条大于给定边的边，最小生成树肯定不变。

设联通块 \(1\) 有 \(a\) 个元素，联通块 \(2\) 有 \(b\) 个元素，给定边长度为 \(w\)，那么两个联通块中的点对就有 \(a\times b -1\) 对（最小生成树里的那对不算），每对点对有不连边、连一条权值为 \(w+1\) 的边、连一条权值为 \(w+1\) 的边 . . . 连一条权值为 \(S\) 的边，一共 \(S-w+1\) 种连法，\(ans=ans\times (S-w+1)^{a+b-1}\)。

跑一遍最小生成树，维护每个联通块的 \(size\) ，再统计答案即可。

没注释的 Code#

#include <bits/stdc++.h>
#define int long long
using namespace std;

struct Edge{
	int u,v,w;
}E[200005];
int T,N,S,X,Y,Z;
int ans;

int Power(int base,int power){
	int res=1;
	while(power){
		if(power&1) res=(res*base)%998244353;
		base=(base*base)%998244353;
		power>>=1;
	}return res;
}

int fa[200005],sz[200005];
int Find(int x){return x==fa[x]?x:fa[x]=Find(fa[x]);}

int Kruskal(){
	ans=1;
	for(int i=1;i<=N;i++) fa[i]=i,sz[i]=1;
	for(int i=1;i<N;i++){
		int u=E[i].u;
		int v=E[i].v;
		int w=E[i].w;
		int a=Find(u);
		int b=Find(v);
		if(a!=b){
			if((w+1)<=S) ans=ans*Power(S-w+1,sz[a]*sz[b]-1)%998244353;
			sz[b]+=sz[a];
			fa[a]=b;
		}
	}return ans;
}

signed main()
{
	scanf("%lld",&T);
	while(T--){
		scanf("%lld%lld",&N,&S);
		for(int i=1;i<N;i++){
			scanf("%lld%lld%lld",&E[i].u,&E[i].v,&E[i].w);
		}sort(E+1,E+N,[](Edge a,Edge b){return a.w<b.w;});
		printf("%lld\n",Kruskal());
	}
	return 0;
}