8.方差分析

单因素方差分析

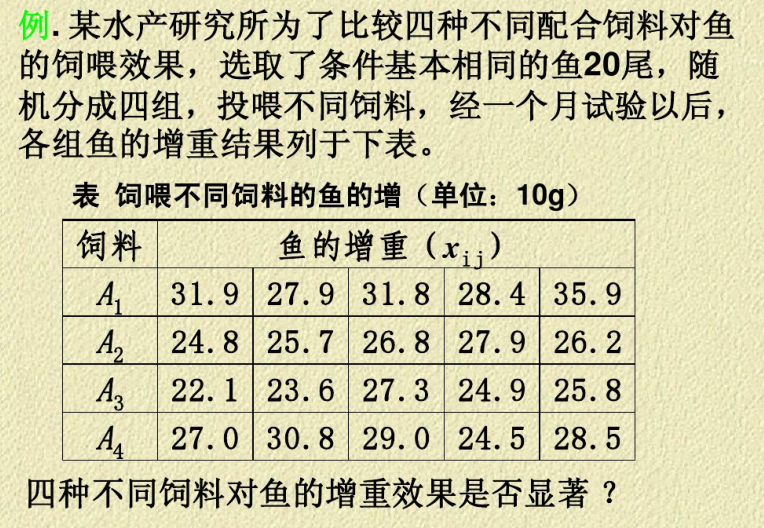
解:这是单因素均衡数据的方差分析，Matlab程序
如下:

A=[31.9 27.9 31.8 28.4 35.9
24.8 25.7 26.8 27.9 26.2 
22.1 23.6 27.3 24.9 25.8
27.0 30.8 29.0 24.5 28.5];
B = A';  %将矩阵转置,Matlab中要求各列为不同水平
p=anova1(B);  

运行结果一表一图。

误差分析表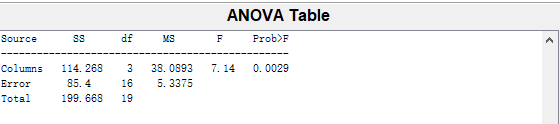

 

 

 含义

 

 

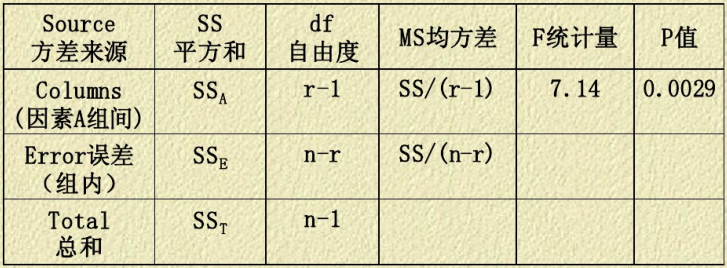
 当p<0.05称差异是显著的，当p<0.01称差异是高度显著的.，因为p=0.0029<0.01, 故不同饲料对鱼的增重效果极为显著. 

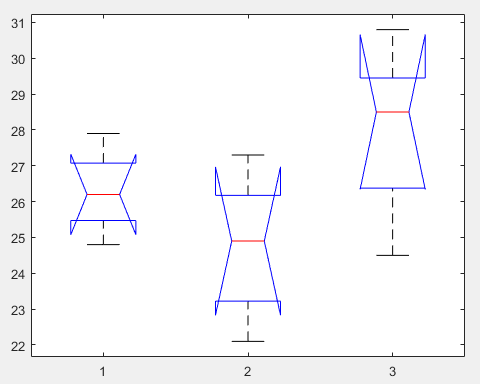
均值盒子图

四种不同饲料对鱼的增重效果极为显著，
那么哪一种最好呢?请看下图 

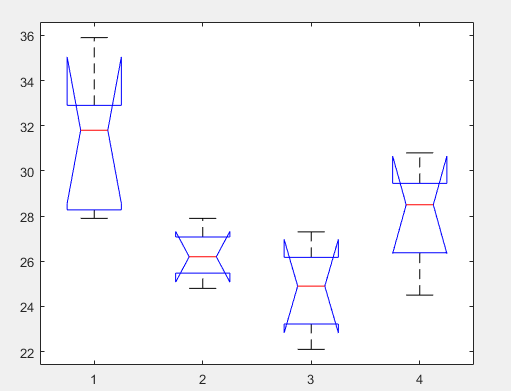
此时，第一个图对应第一种饲料且离盒子图中心线较远，效果最突出。

试验：

如果从原始数据中去掉第一种饲料的试验数据。

p=anova1(B(:,2:4));

 

 

 得到的结果为各种饲料之间对鱼的增重效果不显著.

 单因素非均衡方差分析。

 

 代码

A=[ 164 190 203 205 206 214 228 257 185 197 201 231 187 212 215 220 248 265 281];
group=[1*ones(1,8),2*ones(1 ,4),3*ones(1,7)];
p=anova1(A, group)

 

 

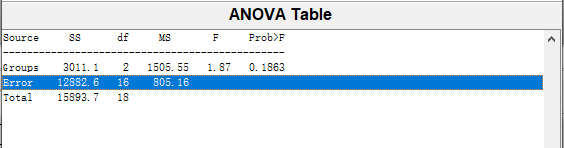
由于概率p=0.1863比较大，故认为三种食料没有显著差异.

多重比较

 

 

 

 从下图 0.0027<0.05 看到

 

 

 

从方差分析表可知:四个实验室生产有差异，那么如何比较?软件输出c如下所示:

 

 

 

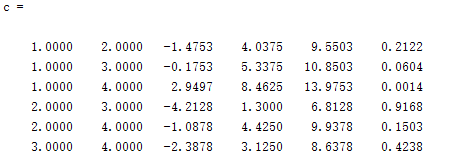
1,2列表示比较的实验室号码，3,5列分别为置信区间左右端点，第4列是均值差的统计量观测值.

若置信区间包含原点则无显著差异，可见只有1,4实验室有显著差异.另外，软件输出一幅图形，告知1, 4有显著差异.

 

 

 

 

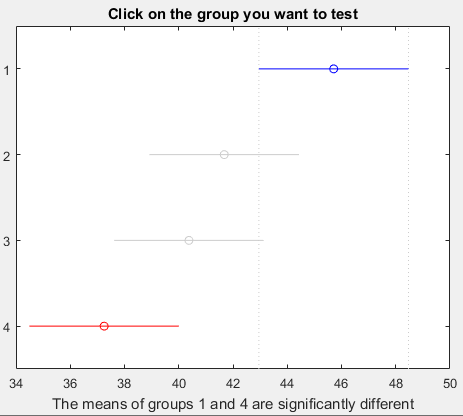
一般，当F>F0.99时，称因子的影响高度显著，记为 ** 
当F0.99>F≥F0.95时，称因子的影响显著，记为 *
当F<F0.95时，称因子无显著影响，即认为因子各水平间无差异.

有交互作用方差分析

 

 

 代码

clc,clear
x0=[58.2,52.6 56.2,41.2 65.3,60.8
49.1,42.8,54.1,50.5 51.6,48.4
60.1,58.3 70.9,73.2 39.2,40.7
75.8, 71.5 58.2,51.0 48.7,41.4] ;
x1=x0(: ,1:2:5) ;x2=x0(: ,2:2:6) ;
for i=1 :4
x(2*i-1,:)=x1(i,:) ;
x(2*i, :)=x2(i, :) ;
end
p=anova2 (x,2)

 

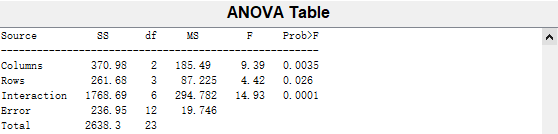
运行结果：

 

 

 

求得p=0.00350.0260 0.001,表明各试验均值相等的概率都为小概率，故可拒绝均值相等假设。即认为不同燃料(因素A)、不同推进器(因素B)下的射程有显著差异，交互作用也是显著的。

 

 

 

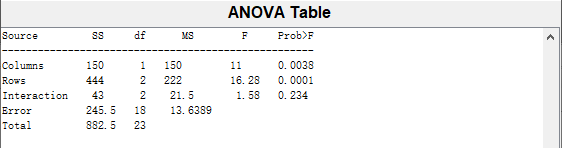
 代码

A=[81,78,79,78 75,80,78,73 82,80,85,88
89,82,77,90 79,80,75,78 93,93,86,95];
[p1,t1,s1]=anova2(A',4);
%为何转置?软件设计重复实验数据按行排列
 

运行结果

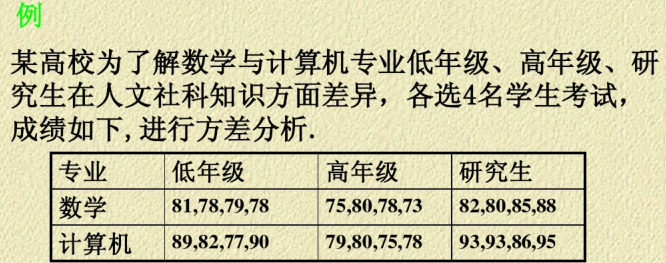
专业与年级的交互效应没有显著差异p=0.234>0.05
两个专业的人文社科水平有显著差异p=0.0038
不同年级之间有显著差异p=0.0001.

 

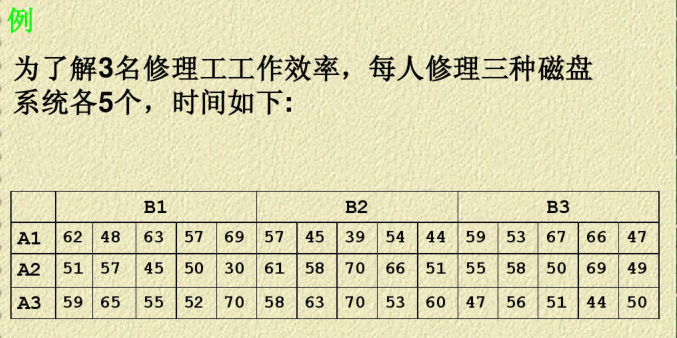
 代码

x=[62 48 63 57 69 57 45 39 54 44 59 53 67 66 47
51 57 45 50 30 61 58 70 66 51 55 58 50 69 49
59 65 55 52 70 58 63 70 53 60 47 56 51 44 50];
p=anova2(x',5);  

运行结果

 

 

结论:只有交互效应有显著差异p=0.001 <0.01.