4.MATLAB 插值法+曲线拟合+逐步分析(习题)
1.插值法

上代码!!!(我抄百度文档上的 https://wenku.baidu.com/view/52e6ad5602768e9950e73814.html)
x=1200:400:4000; y=1200:400:3600; z=[1130 1250 1280 1230 1040 900 500 700; 1320 1450 1420 1400 1300 700 900 850; 1390 1500 1500 1400 900 1100 1060 950; 1500 1200 1100 1350 1450 1200 1150 1010; 1500 1200 1100 1550 1600 1550 1380 1070; 1500 1550 1600 1550 1600 1600 1600 1550; 1480 1500 1550 1510 1430 1300 1200 980]; figure(1); meshz(x,y,z) xlabel('X'),ylabel('Y'),zlabel('Z') title('网格面') xi=1200:40:4000; yi=1200:40:3600; figure(2) z1i=interp2(x,y,z,xi,yi','nearest');%最邻近插值 surfc(xi,yi,z1i) xlabel('X'),ylabel('Y'),zlabel('Z') title('最邻近插值') figure(3) z2i=interp2(x,y,z,xi,yi'); surfc(xi,yi,z2i) xlabel('X'),ylabel('Y'),zlabel('Z')%分段线性插值 title('分段线性插值') figure(4) z3i=interp2(x,y,z,xi,yi','cubic'); surfc(xi,yi,z3i) xlabel('X'),ylabel('Y'),zlabel('Z')%立方插值 title('立方插值') figure(5) z4i=interp2(x,y,z,xi,yi','spline'); surfc(xi,yi,z4i) xlabel('X'),ylabel('Y'),zlabel('Z')%三次样条插值% title('三次样条插值') figure(6) z5i=interp2(x,y,z,xi,yi','linear'); surfc(xi,yi,z4i) xlabel('X'),ylabel('Y'),zlabel('Z')%线性插值 title('线性插值') figure(7) subplot(3,2,1),contour(xi,yi,z1i,10,'r'); subplot(3,2,2),contour(xi,yi,z2i,10,'r'); subplot(3,2,3),contour(xi,yi,z3i,10,'r'); subplot(3,2,4),contour(xi,yi,z4i,10,'r'); subplot(3,2,5),contour(xi,yi,z5i,10,'r');%compare figure(8) contour(xi,yi,z1i,10,'r') title('最邻近插值') figure(9) contour(xi,yi,z2i,10,'r') title('分段线性插值') figure(10) contour(xi,yi,z3i,10,'r') title('立方插值') figure(11) contour(xi,yi,z4i,10,'r') title('三次样条插值') figure(12) contour(xi,yi,z5i,10,'r') title('线性插值')
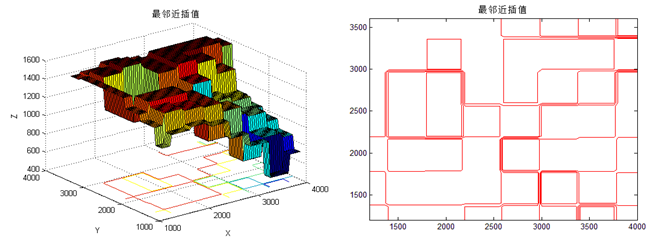




2.曲线拟合
假定某地某天的气温变化记录数据见下表,误差不超过0.5℃,试找出其这一天的气温变化规律。
|
时刻/h |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
温度/℃ |
15 |
14 |
14 |
14 |
14 |
15 |
16 |
18 |
20 |
22 |
23 |
25 |
28 |
31 |
|
时刻/h |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
|
|
温度/℃ |
32 |
31 |
29 |
27 |
25 |
24 |
22 |
20 |
18 |
07 |
16 |
|
|
|
对的温度进行分析,采用多项式拟合的数学方法,建立温度和时刻的模型
x=0:1:24; y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 07 16]; plot(x,y,'r*') hold on a=polyfit(x,y,5); z=a(1)*x.^5+a(2)*x.^4+a(3)*x.^3+a(4)*x.^2+a(5)*x+a(6); plot(x,z) grid; hold off
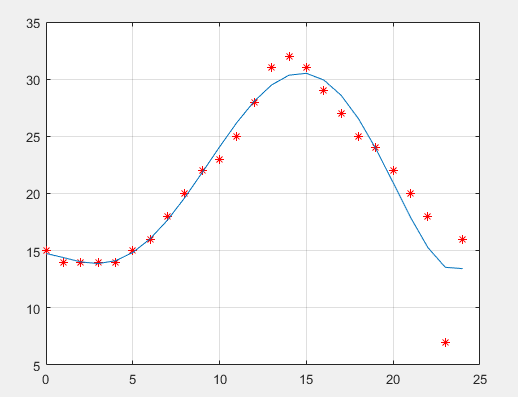
3.逐步回归
财政收入预测问题:财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。下表列出了1952-1981年的原始数据,试构造回归预测模型,并利用1982-1990的数据验证模型。
|
年份 |
国民收入(亿元) |
工业总产值(亿元) |
农业总产值(亿元) |
总人口(万人) |
就业人口(万人) |
固定资产投资(亿元) |
财政收入(亿元) |
|
1952 |
598 |
349 |
461 |
57482 |
20729 |
44 |
184 |
|
1953 |
586 |
455 |
475 |
58796 |
21364 |
89 |
216 |
|
1954 |
707 |
520 |
491 |
60266 |
21832 |
97 |
248 |
|
1955 |
737 |
558 |
529 |
61465 |
22328 |
98 |
254 |
|
1956 |
825 |
715 |
556 |
62828 |
23018 |
150 |
268 |
|
1957 |
837 |
798 |
575 |
64653 |
23711 |
139 |
286 |
|
1958 |
1028 |
1235 |
598 |
65994 |
26600 |
256 |
357 |
|
1959 |
1114 |
1681 |
509 |
67207 |
26173 |
338 |
444 |
|
1960 |
1079 |
1870 |
444 |
66207 |
25880 |
380 |
506 |
|
1961 |
757 |
1156 |
434 |
65859 |
25590 |
138 |
271 |
|
1962 |
677 |
964 |
461 |
67295 |
25110 |
66 |
230 |
|
1963 |
779 |
1046 |
514 |
69172 |
26640 |
85 |
266 |
|
1964 |
943 |
1250 |
584 |
70499 |
27736 |
129 |
323 |
|
1965 |
1152 |
1581 |
632 |
72538 |
28670 |
175 |
393 |
|
1966 |
1322 |
1911 |
687 |
74542 |
29805 |
212 |
466 |
|
1967 |
1249 |
1647 |
697 |
76368 |
30814 |
156 |
352 |
|
1968 |
1187 |
1565 |
680 |
78534 |
31915 |
127 |
303 |
|
1969 |
1372 |
2101 |
688 |
80671 |
33225 |
207 |
447 |
|
1970 |
1638 |
2747 |
767 |
82992 |
34432 |
312 |
564 |
|
1971 |
1780 |
3156 |
790 |
85229 |
35620 |
355 |
638 |
|
1972 |
1833 |
3365 |
789 |
87177 |
35854 |
354 |
658 |
|
1973 |
1978 |
3684 |
855 |
89211 |
36652 |
374 |
691 |
|
1974 |
1993 |
3696 |
891 |
90859 |
37369 |
393 |
655 |
|
1975 |
2121 |
4254 |
932 |
92421 |
38168 |
462 |
692 |
|
1976 |
2052 |
4309 |
955 |
93717 |
38834 |
443 |
657 |
|
1977 |
2189 |
4925 |
971 |
94974 |
39377 |
454 |
723 |
|
1978 |
2475 |
5590 |
1058 |
96259 |
39856 |
550 |
922 |
|
1979 |
2702 |
6065 |
1150 |
97542 |
40581 |
564 |
890 |
|
1980 |
2791 |
6592 |
1194 |
98705 |
41896 |
568 |
826 |
|
1981 |
2927 |
6862 |
1273 |
100072 |
73280 |
496 |
810 |
首先,以国民收入 、工业总产值 、农业总产值 、总人口 、就业人口 、固定资产投资 的数据为全部自变量,采用最小二乘法拟合一个多元回归模型,有
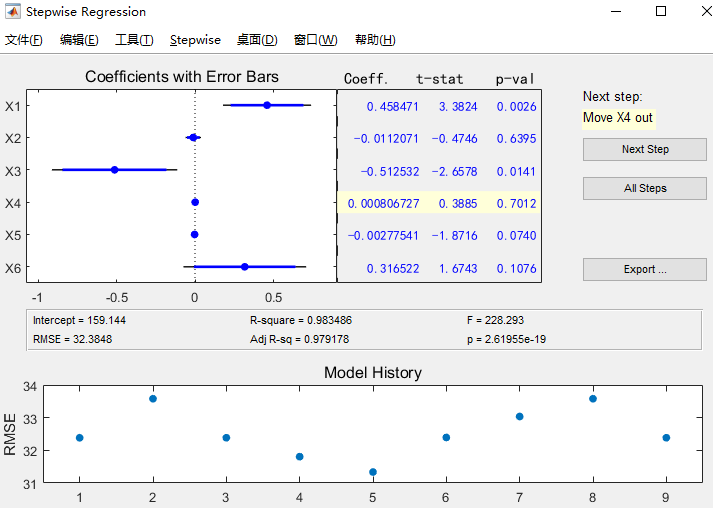

由上述结果得到: 检验通过,复判定系数与调整复判定系数的差距不大;但在t 检验中有若干自变量对y 的解释作用不明显,在此采用逐步回归的方法对自变量集合进行调整。
利用Matlab统计工具箱中用作逐步回归的命令stepwise(一直点Next Step),进行统计分析,得到如图所示的结果:
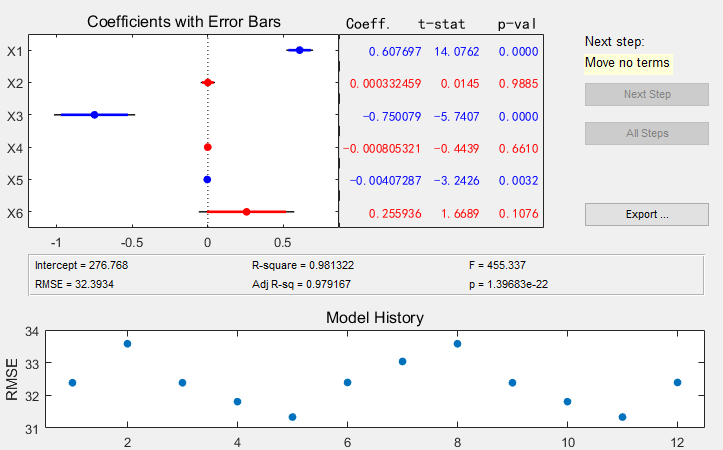
由上图可以看出:红色表明从模型中移去的变量为x2,4,8,移除这三个变量后,再利用最小二乘法拟合一个多元回归模型,有
![]()
两个回归模型相比较,得到:后者的复判定系数与调整复判定系数的差距更小,与实际更加符合,因此所做的调整是有意义的,对于预测更加有利。
代码
多元回归模型建立的程序(没看懂这个是干嘛的,而且运行报错警告: 矩阵接近奇异值,或者缩放错误。结果可能不准确。RCOND = 5.420589e-17。 ):
clc,clear load data.txt %表中的数据按照原来的排列存放在纯文本文件data.txt中 [n,m]=size(data);m=m-1; x=[ones(30,1),data(:,1:6)]; y=data(:,7); [b,bint,r,rint,stats]=regress(y,x) %stats(4)返回的是残差的样本方差 r2=stats(1) %提出复判定系数 ad_r2=1-(1-r2)*(n- 1)/(n-m-1) %计算调整复判断系数 f=stats(2) %提出F统计量 tm=inv(x'*x); %计算X'*X的逆矩阵 tm=diag(tm); %提出逆矩阵的对角线元素 rmse=sqrt(stats(4)) %计算剩余标准差(残差的样本标准差) t=b./sqrt(tm)/ rmse %求t统计量的值
逐步回归代码
clc,clear x0=[1952 598 349 461 57482 20729 44 184 1953 586 455 475 58796 21364 89 216 1954 707 520 491 60266 21832 97 248 1955 737 558 529 61465 22328 98 254 1956 825 715 556 62828 23018 150 268 1957 837 798 575 64653 23711 139 286 1958 1028 1235 598 65994 26600 256 357 1959 1114 1681 509 67207 26173 338 444 1960 1079 1870 444 66207 25880 380 506 1961 757 1156 434 65859 25590 138 271 1962 677 964 461 67295 25110 66 230 1963 779 1046 514 69172 26640 85 266 1964 943 1250 584 70499 27736 129 323 1965 1152 1581 632 72538 28670 175 393 1966 1322 1911 687 74542 29805 212 466 1967 1249 1647 697 76368 30814 156 352 1968 1187 1565 680 78534 31915 127 303 1969 1372 2101 688 80671 33225 207 447 1970 1638 2747 767 82992 34432 312 564 1971 1780 3156 790 85229 35620 355 638 1972 1833 3365 789 87177 35854 354 658 1973 1978 3684 855 89211 36652 374 691 1974 1993 3696 891 90859 37369 393 655 1975 2121 4254 932 92421 38168 462 692 1976 2052 4309 955 93717 38834 443 657 1977 2189 4925 971 94974 39377 454 723 1978 2475 5590 1058 96259 39856 550 922 1979 2702 6065 1150 97542 40581 564 890 1980 2791 6592 1194 98705 41896 568 826 1981 2927 6862 1273 100072 73280 496 810]; x=x0(:,2:7); y=x0(:,8); stepwise(x,y,[1:6])
4.



