一道有趣的组合数学问题

背景：这道题原先是之前一次练习的问题，当时自己推公式推了很久
最后看题解发现是一道组合数学问题，给了自己很多启发，特此记录

原题链接
简单描述题意就是给定一个矩形区域的长和宽（设定为n,m)，要求在这个区域内选择一个大矩形和一个小矩形
小矩形必须在大矩形的内部
并且这个矩形的长和宽不能和大矩形重合

大致图就是这样吧

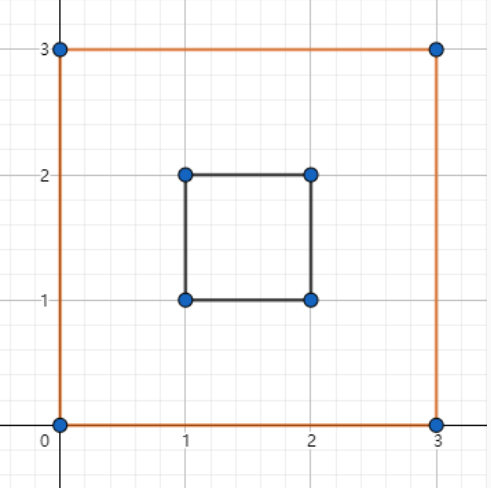
当时自己推了很久的公式，先固定大矩形的长然后巴拉巴拉，再固定大矩形的宽巴拉巴拉
中间还要找到相邻项的关系，合并成一个公式，最后两个结果相乘。
不得不说非常复杂

但是这个问题其实抽象化了会变成一个很简单的问题

相当于原问题可以转化为在n+1个点中选4个点和在m+1个点中选4个点
因为需要考虑坐标轴，所以是n+1和m+1
这4个点就对应小矩形和大矩形的行，小矩形和大矩形的列。
相当于把每个合法答案的小矩形和大矩形的边长抽象出来对应于每个组合
所以最后的答案就是
\({n+1 \choose 4} \times {m+1 \choose 4}\)