牛客小白月赛57

A

思路

问两个矩形重叠的最大面积，显然我们把两个矩形的左下角对齐，形成的重叠部分面积即是最大面积

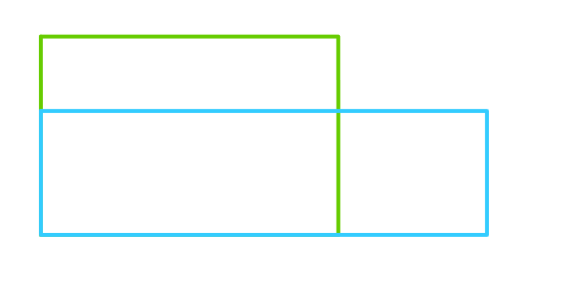
所以答案就是长的最小值*宽的最小值

代码

//                  ξ†(ᗜ ˰ ᗜ)†ξ
//           去吧，鸭鸭，把希儿和AC都带回来！
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int a,b,c,d;
    cin >> a >> b >> c >> d;
    cout << min(a,c) * min(b,d) << endl;
    return 0;
}

B

思路

简单的思维题，可以发现答案最多不会超过2
分3种情况考虑

每一块地都有树显然这时候我们不需要进行任何操作
只有部分地面有树，判断首尾的情况，如果有树，则只用操作一次
首尾都没树，这个时候必须要走两次（方向不一样）才能走完

代码

//                  ξ†(ᗜ ˰ ᗜ)†ξ
//           去吧，鸭鸭，把希儿和AC都带回来！
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    string s;
    cin >> n;
    cin >> s;
    int p = 0;
    for(int i = 0; i < (int)s.size(); i++){
        if(s[i] == '1') p++;
    }
    if(p == n) cout << 0 << endl;
    else if(s[0] == '1' || s[n-1] == '1') cout << 1 << endl;
    else cout << 2 << endl;
    return 0;
}

C

思路

有点恶心的思维+模拟题，细节有点多
也是分情况讨论

$a == b$ 我们不需要做任何操作
$a < b$ 那么又会有如下情况
1. $a + k < b$ 我们可以直接从 $a$ 一步跳到 $b$
2. $a - k - 1 > 0$ 如果一步跳不到，我们可以先往下走 $k+1$ 步，这样一定能跳到
3. $b + k + 1 <= n$ 我们可以直接从 $a$ 跳到 $b+k+1$ 再跳到 $b$
4. $a + k + 1 <= n$ 我们可以先跳到 $n$
  如果此时 $b - k - 1 > 0$ 那我们可以从 $n$ 跳到 $b-k-1$ 再跳到 $b$
  如果不满足就无解
  其余情况也无解
$a > b$ 从 $a$ 到 $b$ 和从 $b$ 到 $a$ 的过程是可逆的，交换一下即可

代码

//                  ξ†(ᗜ ˰ ᗜ)†ξ
//           去吧，鸭鸭，把希儿和AC都带回来！
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(int x)
{
    if (x < 0)
    {
        putchar('-');
        x = -x;
    }
    if (x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        int n, k, a, b;
        cin >> n >> k >> a >> b;
        if(a > b){
            int temp = b;
            b = a;
            a = temp;
        }
        if (a == b)
            cout << "YES" << endl;
        else
        {
            if (a + k < b)
                cout << "YES" << endl;
            else if (a - k - 1 > 0)
                cout << "YES" << endl;
            else if (b + k + 1 <= n)
                cout << "YES" << endl;
            else if(a + k + 1 <= n){
                int x = b - k - 1;
                if(x > 0) cout << "YES" << endl;
                else cout << "NO" << endl;
            }
            else
                cout << "NO" << endl;
        }
       
    }
    return 0;
}

D

思路

看到数据范围是 $10^6$, 暴力的解法是 $O(n^2)$
考虑如何去优化
我们可以知道答案一定在 $10^6$ 以内，关键在于看是否是其因子
如果某个数是它的因子，那必然也是它的倍数
我们可以先把每个数出现的次数存起来，直接 O(logn)的时间枚举看是否是其倍数就行
时间复杂度 $O(nlogn)$

代码

//                  ξ†(ᗜ ˰ ᗜ)†ξ
//           去吧，鸭鸭，把希儿和AC都带回来！
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 1e6 + 5;
int a[N];
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int x = 1e6;
    int res = 0;
    for(int i = 1; i <= n; i++) {
        int p;
        cin >> p;
        a[p]++;
    }
    for(int i = 1; i <= x; i++){
        int ans = 0;
        for(int j = 1; j*i <= x; j++){
            ans += a[j*i];
            if(ans >= 2){
                res = i;
                break;
            }
        }
    }
    cout << res << endl;
    return 0;
}

E

思路

可以发现输入的数非常大，只能用string储存
但同时也可以知道所有的有效数字不会超过 $2^{23}$
所以我们直接枚举即可

代码

//                  ξ†(ᗜ ˰ ᗜ)†ξ
//           去吧，鸭鸭，把希儿和AC都带回来！
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int c[25];
bool flag = false;
bool check(string s,int p){
    int temp = p;
    int ws = 0;
    int ls = 0;
    while(temp) {
        ws++;
        c[ws] = temp & 1;
        if(temp & 1 == 1) ls++;
        else ls = 0;
        if(ls >= 3) flag = 1;

        temp >>= 1;
    }
    int x = s.size();
    if(x > ws) return true;
    else if(x == ws){
        
        for(int i = 0; i < x; i++){
            int q =  s[i] - 48;
            if(q < c[ws]) return false;
            else if(q > c[ws]) return true;
            else ws--;
        }
        return true;
    }
    else return false;
    
}

inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    string s;
    cin >> s;
    int sz = s.size();
    int res = 0;
    for(int i = 1; i < 1 << sz; i++){
        flag = false;
        if(check(s,i) && flag) res++;//满足小于s并且至少有3个连续的1
    }
    cout << res << endl;
    return 0;
}

F

思路

可以知道每次我们都能直接选择区间 $[1,n]$ 这样之前已经满足的数不会改变，并且不会影响到答案
很容易想到暴力解法 $O(n\times p)$
考虑如何优化
举几个例子可以发现答案肯定和差值有关
比如
p = 5
3 3 1 4
2 1 3 2
差值为
4 3 2 3
设差值为 $y$
我们只需要找到一个最小的 $x$ ，使得 $k \times y \equiv x \pmod{p} $
化简一下可知 $k \equiv x \times y ^ {p-2} \pmod{p} $
差值最多只有p种,时间复杂度就简化为 $O(p \times p)$
每一次循环找到k的最大值，再求最大值最小

代码

//                  ξ†(ᗜ ˰ ᗜ)†ξ
//           去吧，鸭鸭，把希儿和AC都带回来！
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 1e6 + 5;
int a[N];
int b[N];
bool vis[3505];
vector<int> res;
int qmi(int a,int b){
    int p1 = b + 2;
    int res = 1;
    while(b){
        if(b & 1) res = res * a % p1;
        a = a * a % p1;
        b >>= 1;
    }
    return res;
}
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n,p;
    cin >> n >> p;
    for(int i = 1; i <= n; i++) cin >> a[i];
    for(int i = 1; i <= n; i++) cin >> b[i];
    for(int i = 1; i <= n; i++){
        a[i] %= p;
        if(b[i] - a[i] >= 0) b[i] = b[i] - a[i];
        else b[i] = b[i] - a[i] + p;
        if(!vis[b[i]]){
            res.push_back(b[i]);
            vis[b[i]] = true;
        }
    }
    int sz = res.size();
    if(sz == 1 && res[0] == 0){
        cout << 0 << endl;
        return 0;
    }
    int k = 0x3f3f3f3f;
    int ans = 0;
    for(int i = p-1; i >= 1; i--){
        int m1 = -1,m2 = 0;
        int temp = qmi(i,p-2);
        for(int j = 0; j < sz; j++){
            int x = res[j];
            int x1 = temp;
            x1 = x1 * x % p;
            if(x1 > m1) {
                m1 = x1;
            }
        }
        if(m1 <= k) {
            k = m1;
            ans = i;
        }
    }
    cout << ans << endl;
    return 0;
}

posted @ 2022-09-17 15:31 Sun-Wind 阅读(86) 评论(0) 编辑收藏举报

刷新页面返回顶部

牛客小白月赛57

A

思路

代码

B

思路

代码

C

思路

代码

D

思路

代码

E

思路

代码

F

思路

代码

公告