至至子的公司排队

题目

牛客小白月赛55

思路

这道题抽象化之后就是，给定 \(n\) 个序列
每个序列的数量就是他的拓扑序方案数，将这 \(n\) 个序列进行排列，求总共可形成的方案
我们先思考怎么求一个序列的拓扑序方案数

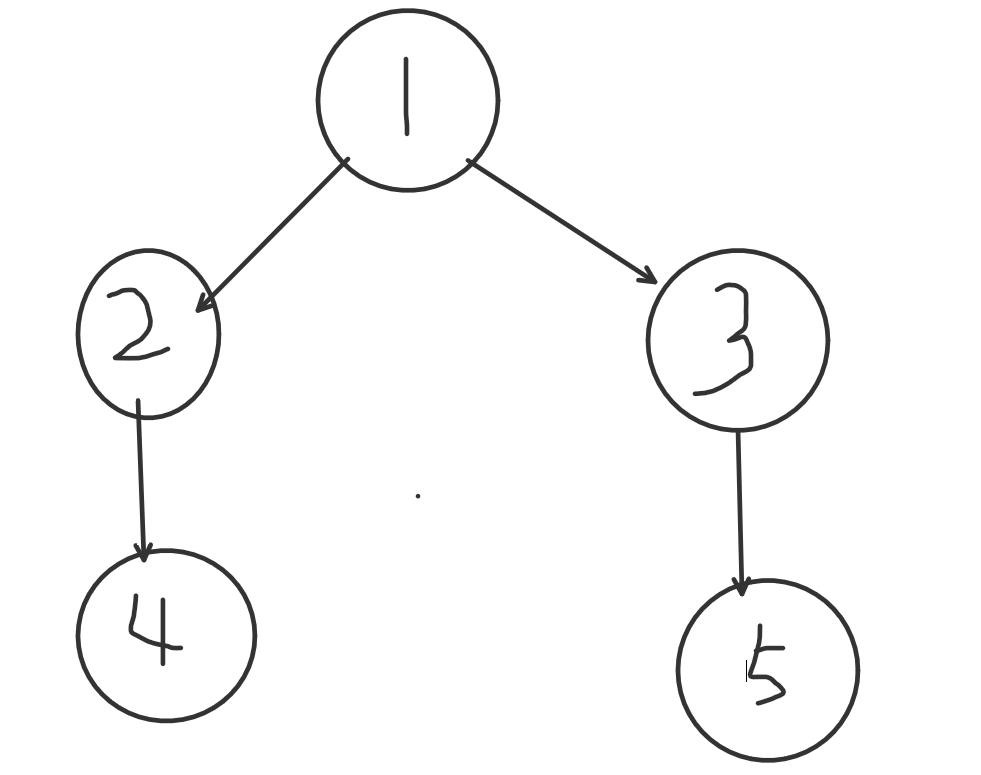
如上图所示，我们从叶子结点向上递推，显然以2号结点为根和以3号结点为根对应的拓扑序数为1
考虑1号结点时就会有下面的情况，蓝色表示以2号结点为根，绿色表示以3号结点为根
同种颜色同种类型

那么方案数就是可重集排列的方案数
如何求可重集的排列?
如{1,2,2,3,3,3,4,4,4,4}
我们可以先考虑它的全排列数为10!,其中重复的数分别有2个，3个，4个
那么除以重复的数所组成的方案数就是\(\frac{10!}{(2!\times3!\times4!)}\)
每一种颜色还代表它的拓扑序数量
用 \(dp[x]\) 表示以 \(x\) 为根结点的拓扑序方案数, \(sz[x]\) 表示以x为根结点的树的总共结点数
那么就会有

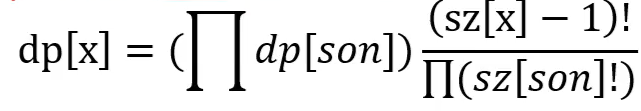
进行树形dp即可

代码

参考版

复制版

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 1e9 + 7;
const int N = 1e5 + 5;
int res = 1;
int dp[N];
int sz[N];
int sp[N];
int head[N];
struct edge{
    int b,w,ne;
}edge[2*N];
int cnt = 1;
int qmi(int a,int b){
    int r = 1;
    while(b){
        if(b & 1){
            r = r * a % M;
        }
        a = a * a % M;
        b >>= 1;
    }
    return r;
}
void add(int a,int b,int c){
    edge[cnt].b = b;
    edge[cnt].w = c;
    edge[cnt].ne = head[a];
    head[a] = cnt++;
}
int dfs(int x,int fa){
    for(int i = head[x]; i != 0; i = edge[i].ne){
        int j = edge[i].b;
        if(j == fa) continue;
        sz[x] += dfs(j,x);
    }
    return sz[x] = sz[x] + 1;
}
int idfs(int x,int fa){
    int p = 1;
    for(int i = head[x]; i != 0; i = edge[i].ne){
        int b = edge[i].b;
        if(b == fa) continue;
        p = (p * idfs(b,fa)) % M;
        p = (p * qmi(sp[sz[b]],M-2)) % M;
    }
    dp[x] = p * sp[(sz[x] - 1)] % M;
    return dp[x];
}
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    sp[0] = 1;
    for(int i = 1; i < N; i++){
        sp[i] = i * sp[i-1] % M;
    }
    int n;
    n = read();
    int ans = 0;
    for(int i = 1; i <= n; i++){
        cnt = 1;
        int x;
        x = read();
        for(int j = 2;j <= x; j++){
            int p = read();
            add(p,j,1);
        }
        dfs(1,0);
        idfs(1,0);
        res = res * dp[1] % M;
        ans += sz[1];
        res = res * qmi(sp[sz[1]],M-2) % M;
        for(int j = 1; j <= x; j++) head[j] = 0,sz[j] = 0,dp[j] = 0;
    }
    res = res * sp[ans] % M;
    print(res);
    printf("\n");
    return 0;
}