“科林明伦杯”哈尔滨理工大学暑假训练赛

G

思路

签到题
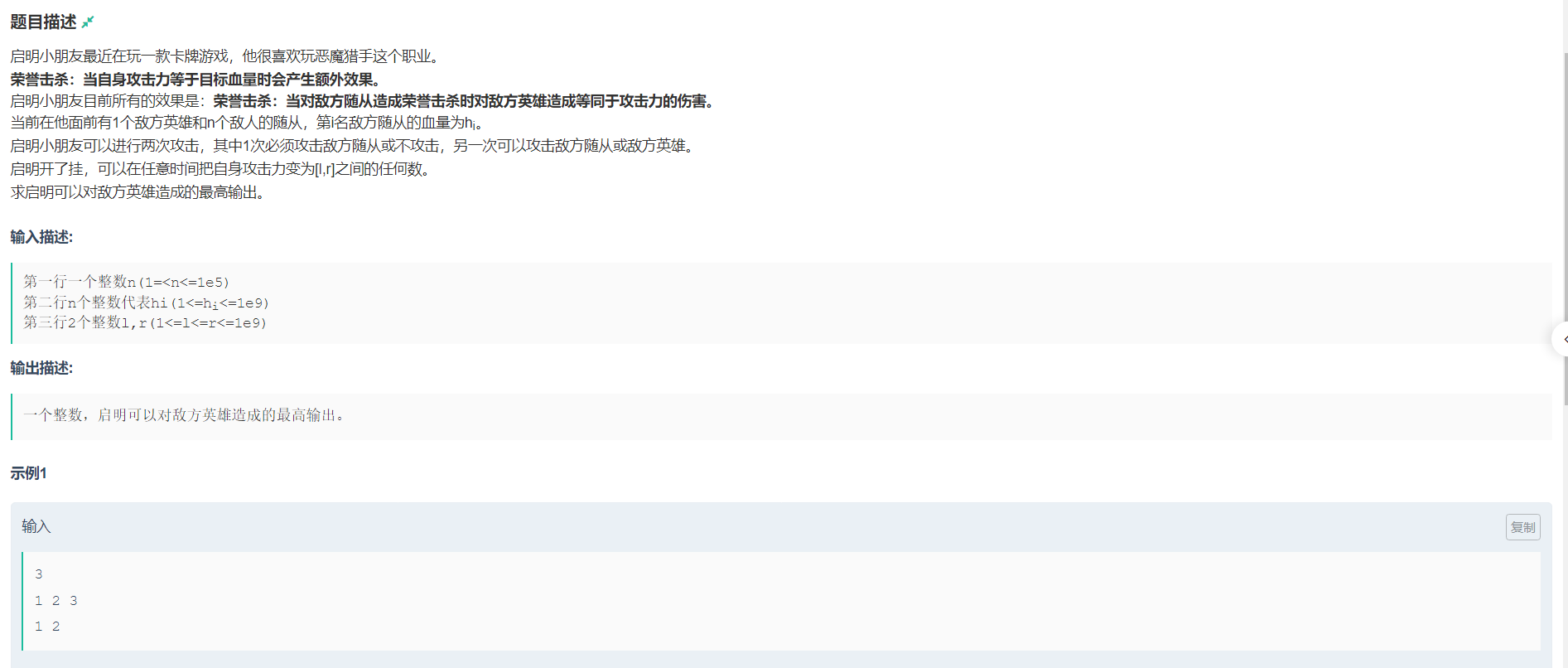
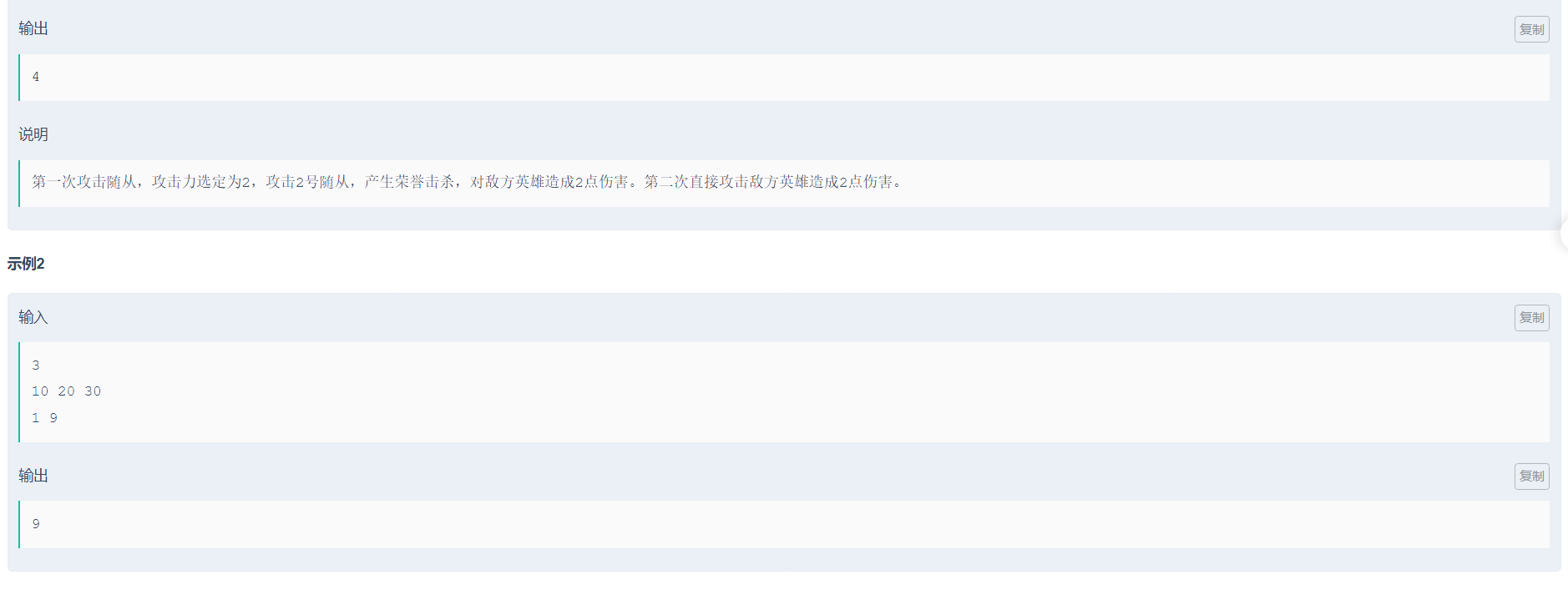
只能攻击两次，第一次攻击尽量触发最高的荣誉击杀（即在给定的数钟找到l到r之间最大的数）
第二次攻击显然只能取得r才能造成最大伤害

代码

非复制版

可复制版

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 1e5 + 5;
int s[N];
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
}
int maxx = 0;
signed main(){
    int n;
    n = read();
    for(int i = 1; i <= n; i++)
    {
        s[i] = read();
    }
    int l,r;
    l = read();
    r = read();
    int maxx = 0;
    for(int i = 1; i <= n; i++){
        if(s[i] >= l && s[i] <= r){
            maxx = max(maxx,s[i]);
        }
    }
    int res = maxx + r;
    print(res);
    printf("\n");
    return 0;
}

A

思路

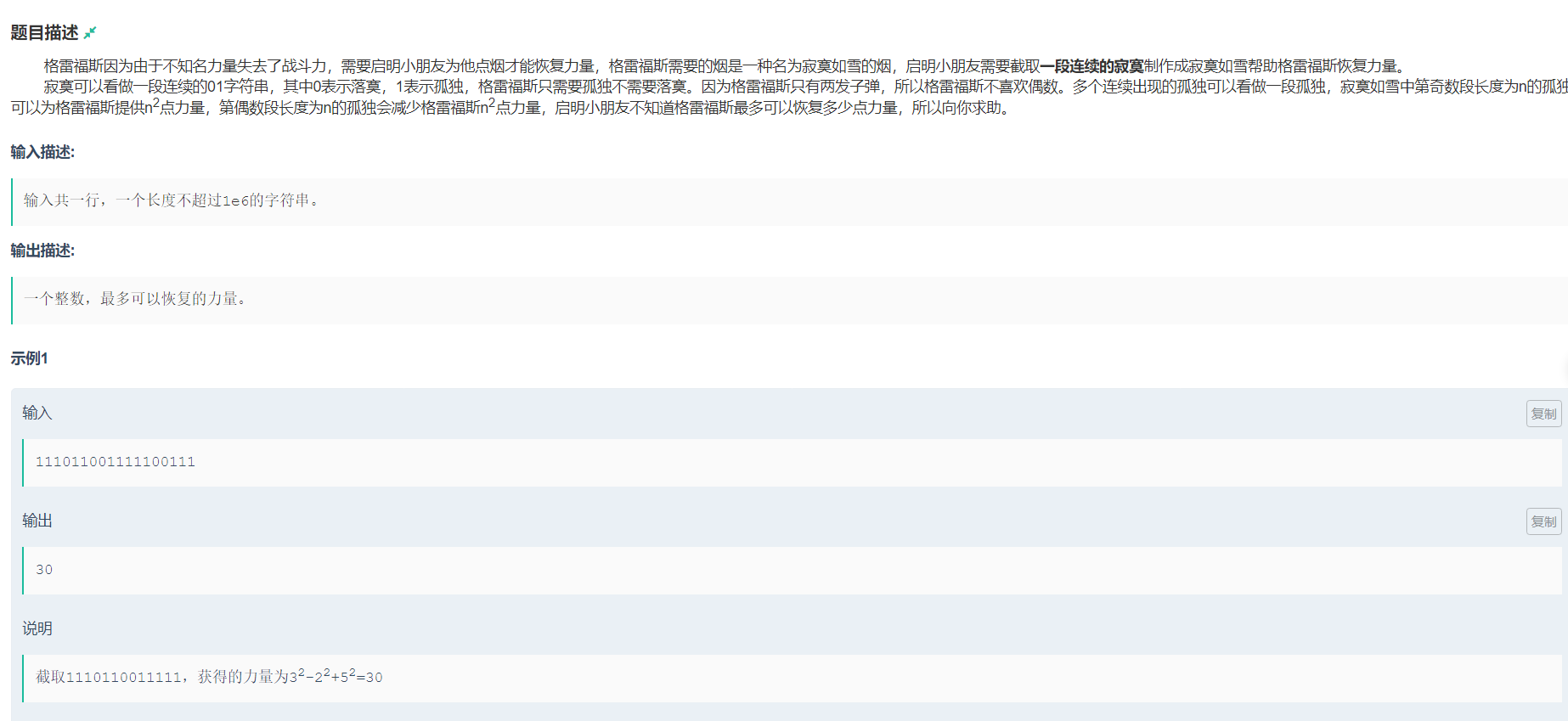
首先预处理出每一段连续的1的权值（用ss数组表示）
容易知道基数段一定比偶数段最优（因为偶数段最后一端是负权值）
所以dp[i]表示以第i个位置结尾最优的连续奇数段权值
那么转移方程就是dp[i] = max(ss[i],dp[i-2] - ss[i-1] + ss[i]);
遍历一遍即可得到答案

代码

非复制版

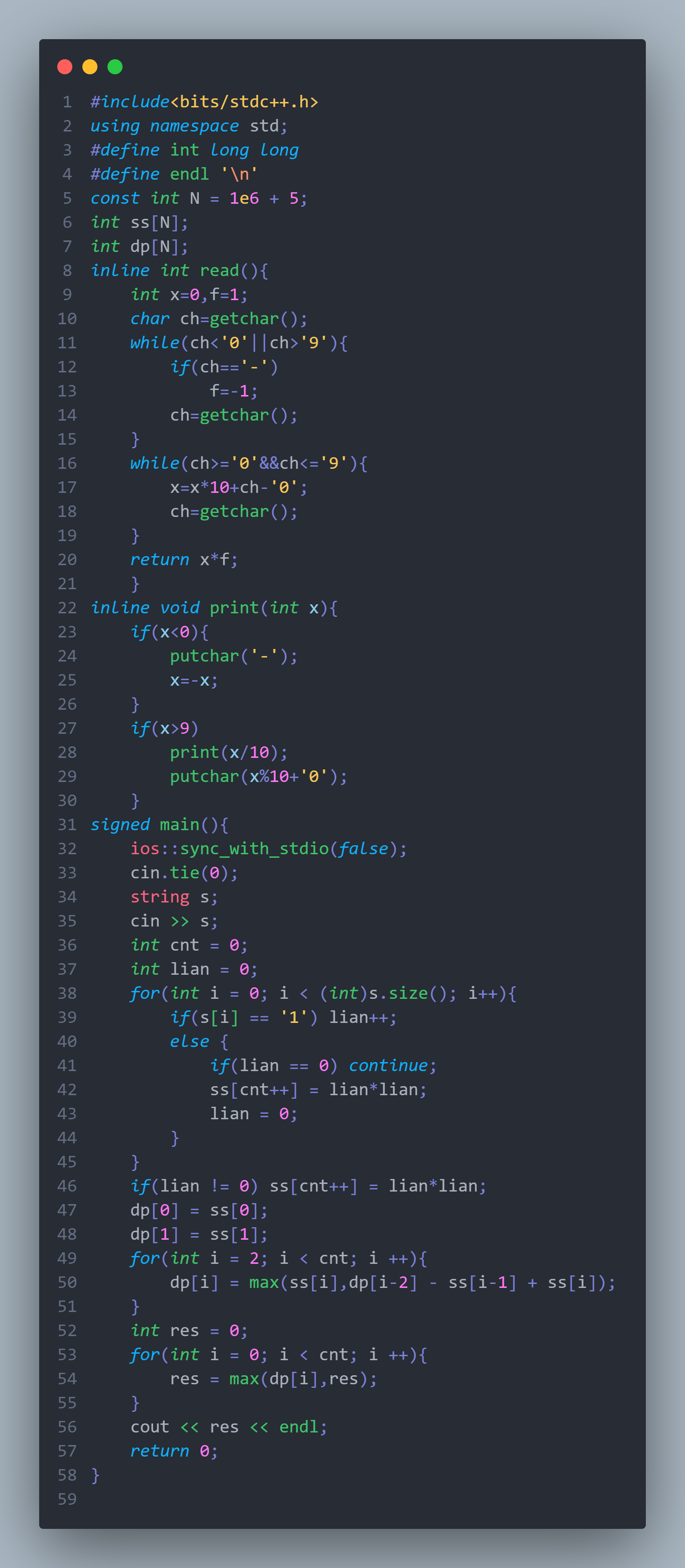
可复制版

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 1e6 + 5;
int ss[N];
int dp[N];
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    string s;
    cin >> s;
    int cnt = 0;
    int lian = 0;
    for(int i = 0; i < (int)s.size(); i++){
        if(s[i] == '1') lian++;
        else {
            if(lian == 0) continue;
            ss[cnt++] = lian*lian;
            lian = 0;
        }
    }
    if(lian != 0) ss[cnt++] = lian*lian;
    dp[0] = ss[0];
    dp[1] = ss[1];
    for(int i = 2; i < cnt; i ++){
        dp[i] = max(ss[i],dp[i-2] - ss[i-1] + ss[i]);
    }
    int res = 0;
    for(int i = 0; i < cnt; i ++){
        res = max(dp[i],res);
    }
    cout << res << endl;
    return 0;
}

B

思路

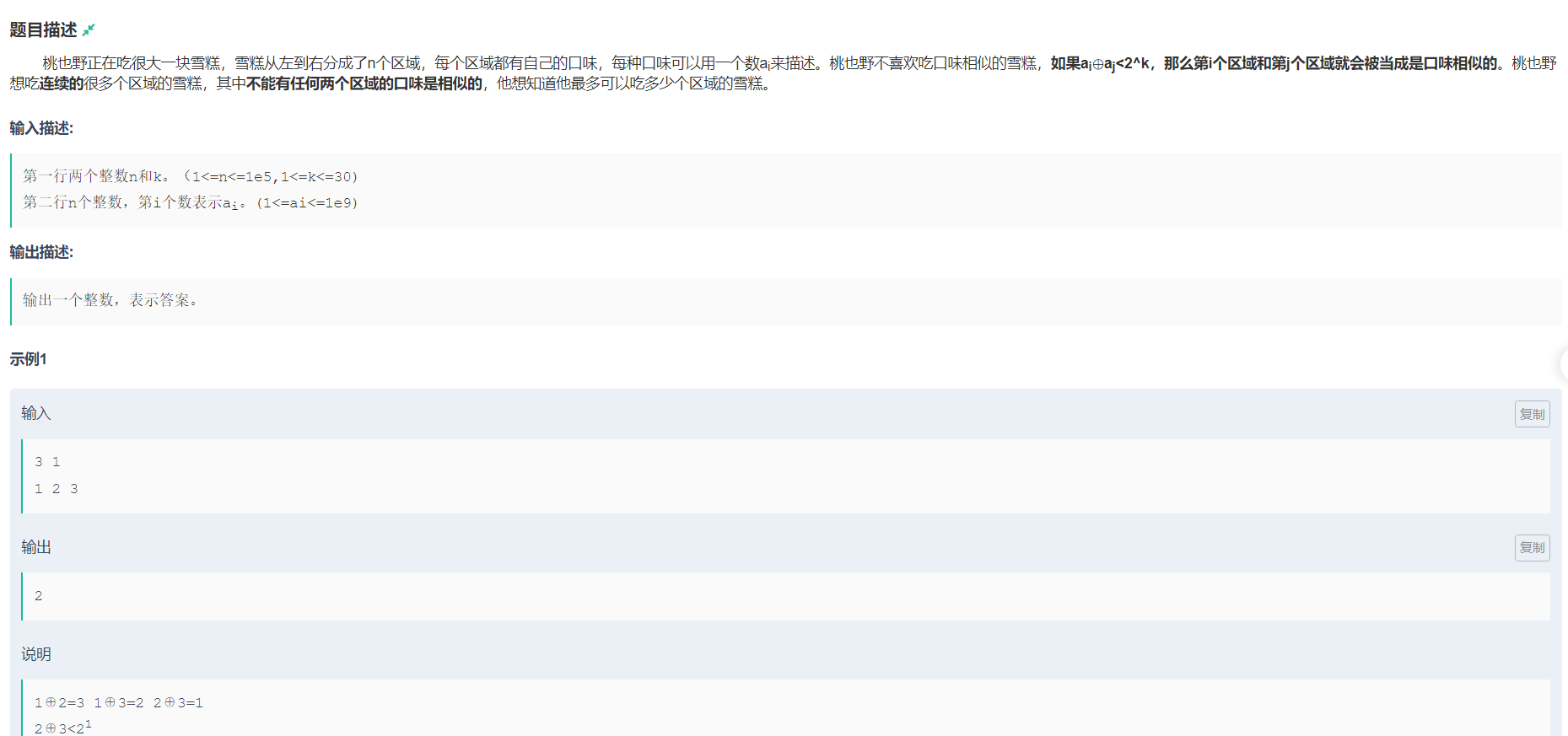
可以先枚举出相似的情况
如果两个数都大于等于2^k，显然决定他们是否相似的只有第k位前面的数。
如果第k位前面的数都相同，则异或以后肯定 < 2^k;
那么我们就可以先将这样的数右移动k位，改变后的数不能出现2次及以上
如果两个数都小于2^k，则这两个数必然会相似，预处理都置为-1
其他位置的数都置为0
这样问题就转化为，在一个数组中找到最长的序列，同一个正数不能出现两次及以上，负数不能多于两个及以上
利用双指针扫描一遍即可

代码

非复制版

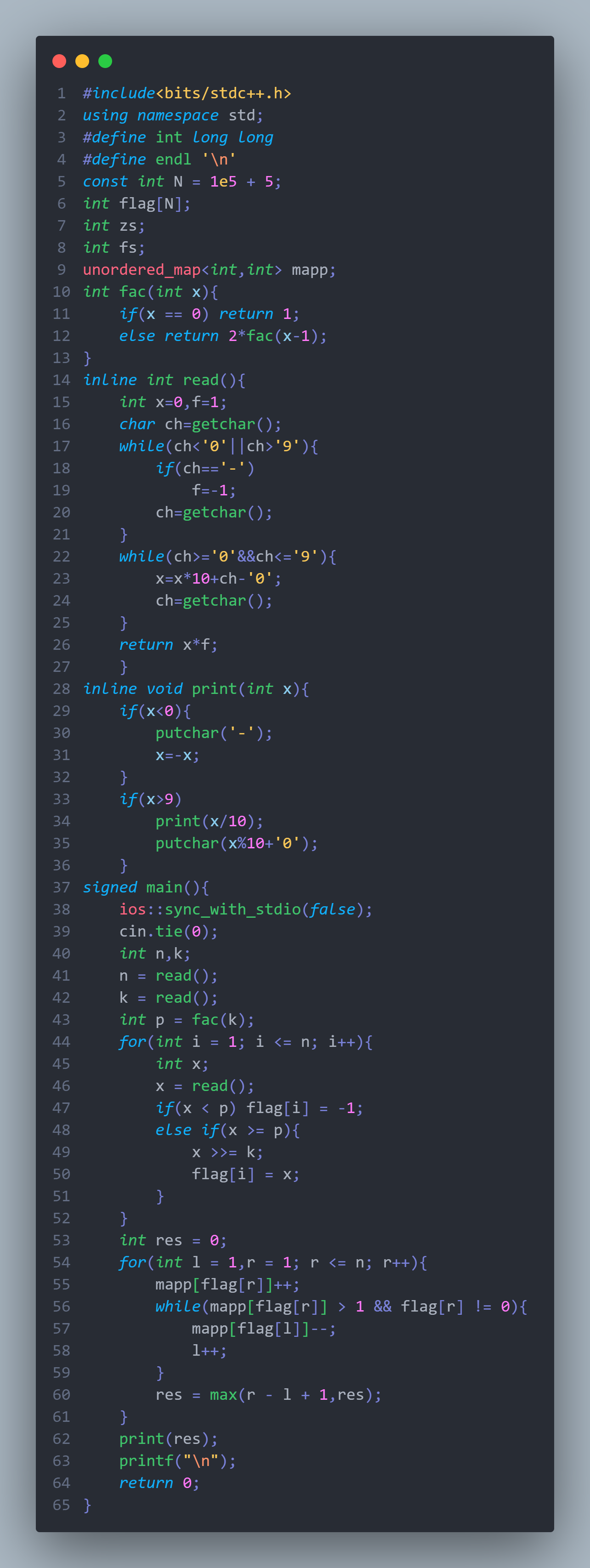
可复制版

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 1e5 + 5;
int flag[N];
int zs;
int fs;
unordered_map<int,int> mapp;
int fac(int x){
    if(x == 0) return 1;
    else return 2*fac(x-1);
}
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n,k;
    n = read();
    k = read();
    int p = fac(k);
    for(int i = 1; i <= n; i++){
        int x;
        x = read();
        if(x < p) flag[i] = -1;
        else if(x >= p){
            x >>= k;
            flag[i] = x;
        }
    }
    int res = 0;
    for(int l = 1,r = 1; r <= n; r++){
        mapp[flag[r]]++;
        while(mapp[flag[r]] > 1 && flag[r] != 0){
            mapp[flag[l]]--;
            l++;
        }
        res = max(r - l + 1,res);
    }
    print(res);
    printf("\n");
    return 0;
}

F

思路

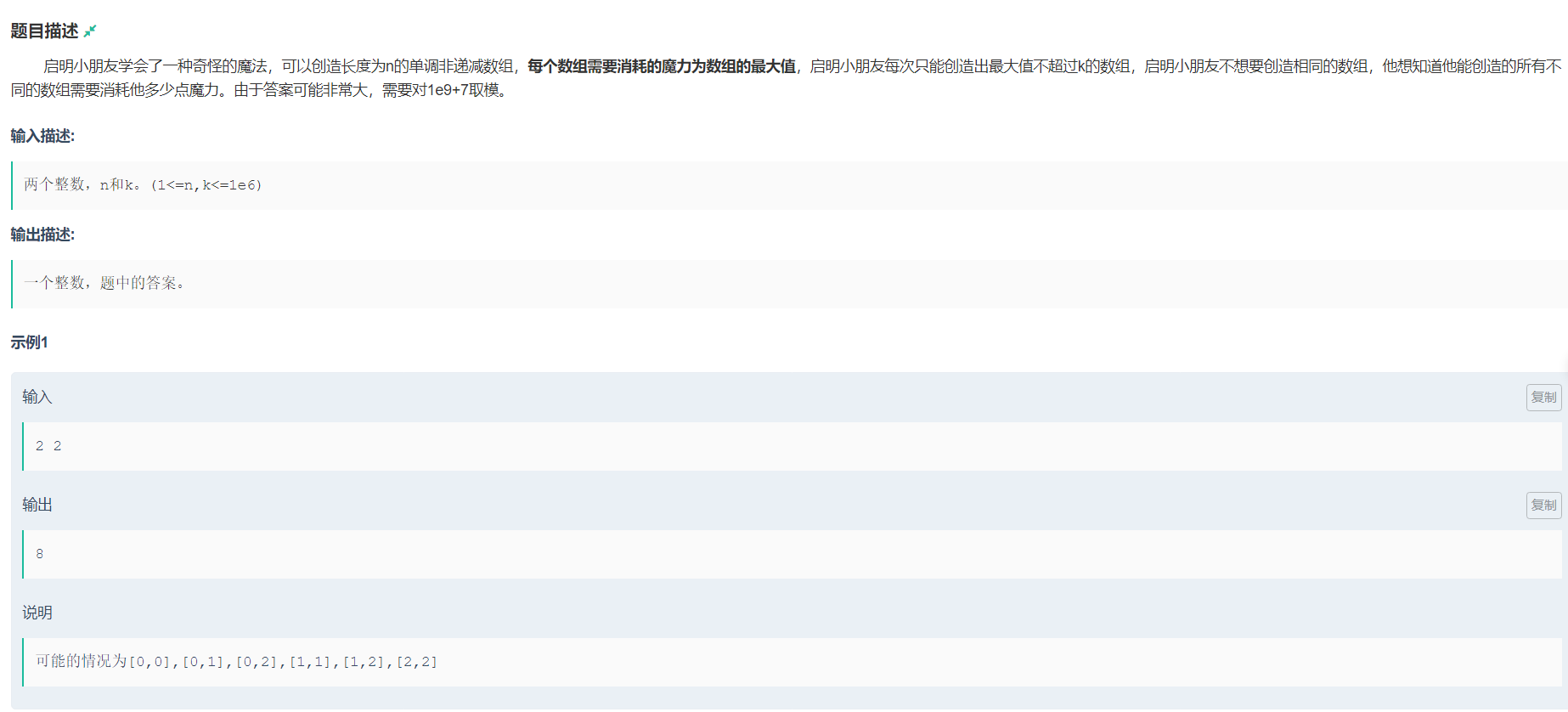
\[我们可以设在这一段序列中，0的个数有x_0个，1的个数有x_1个，k的个数有x_k个 \]

\[显然有x_0 + x_1 + x_2 + ... + x_k = n \]

未知数的取值范围是0~n，找到满足方程的解有多少个
相当于把这个序列分成k+1个部分，可以利用隔板法解决
因为有些未知数可以为0，但是隔板法不能解决中间没有1的情况
如果分成k+1个部分，要插入k个板子，假定每个板子中间有一个球，中间为空的问题就可以解决了

\[原问题转化为C{^k_{n+k-1}} \]

从1到k枚举k即可

代码

非复制版

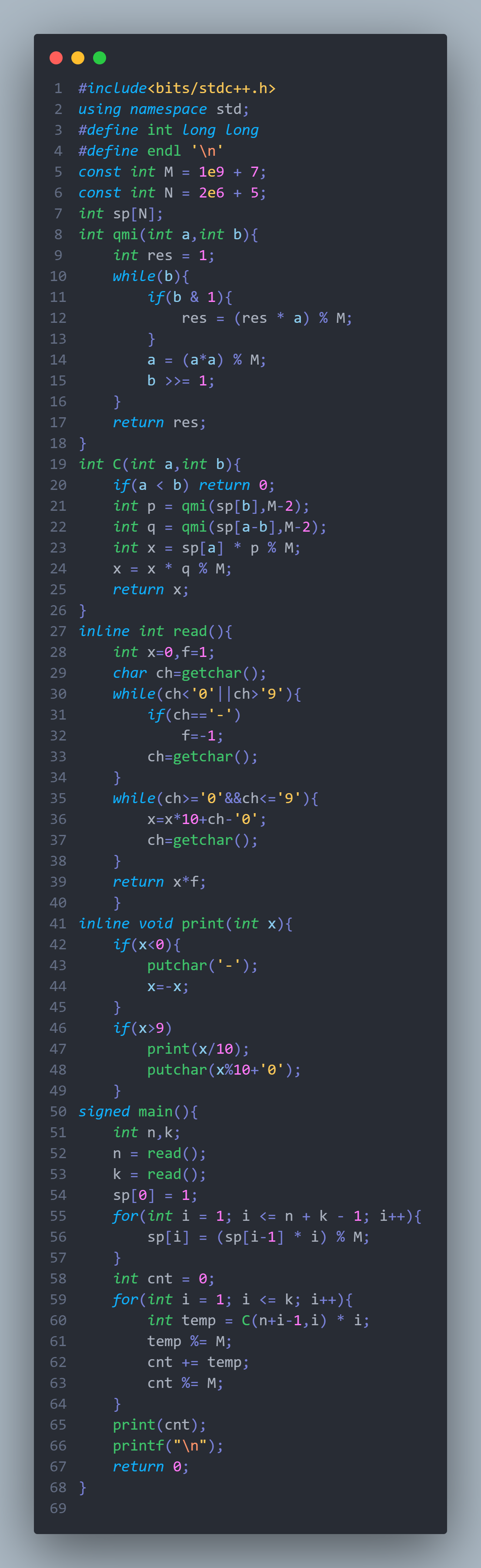
可复制版

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 1e9 + 7;
const int N = 2e6 + 5;
int sp[N];
int qmi(int a,int b){
    int res = 1;
    while(b){
        if(b & 1){
            res = (res * a) % M;
        }
        a = (a*a) % M;
        b >>= 1;
    }
    return res;
}
int C(int a,int b){
    if(a < b) return 0;
    int p = qmi(sp[b],M-2);
    int q = qmi(sp[a-b],M-2);
    int x = sp[a] * p % M;
    x = x * q % M;
    return x;
}
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
    }
inline void print(int x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
        putchar(x%10+'0');
    }
signed main(){
    int n,k;
    n = read();
    k = read();
    sp[0] = 1;
    for(int i = 1; i <= n + k - 1; i++){
        sp[i] = (sp[i-1] * i) % M;
    }
    int cnt = 0;
    for(int i = 1; i <= k; i++){
        int temp = C(n+i-1,i) * i;
        temp %= M;
        cnt += temp;
        cnt %= M;
    }
    print(cnt);
    printf("\n");
    return 0;
}