cf edu 133 D

题意

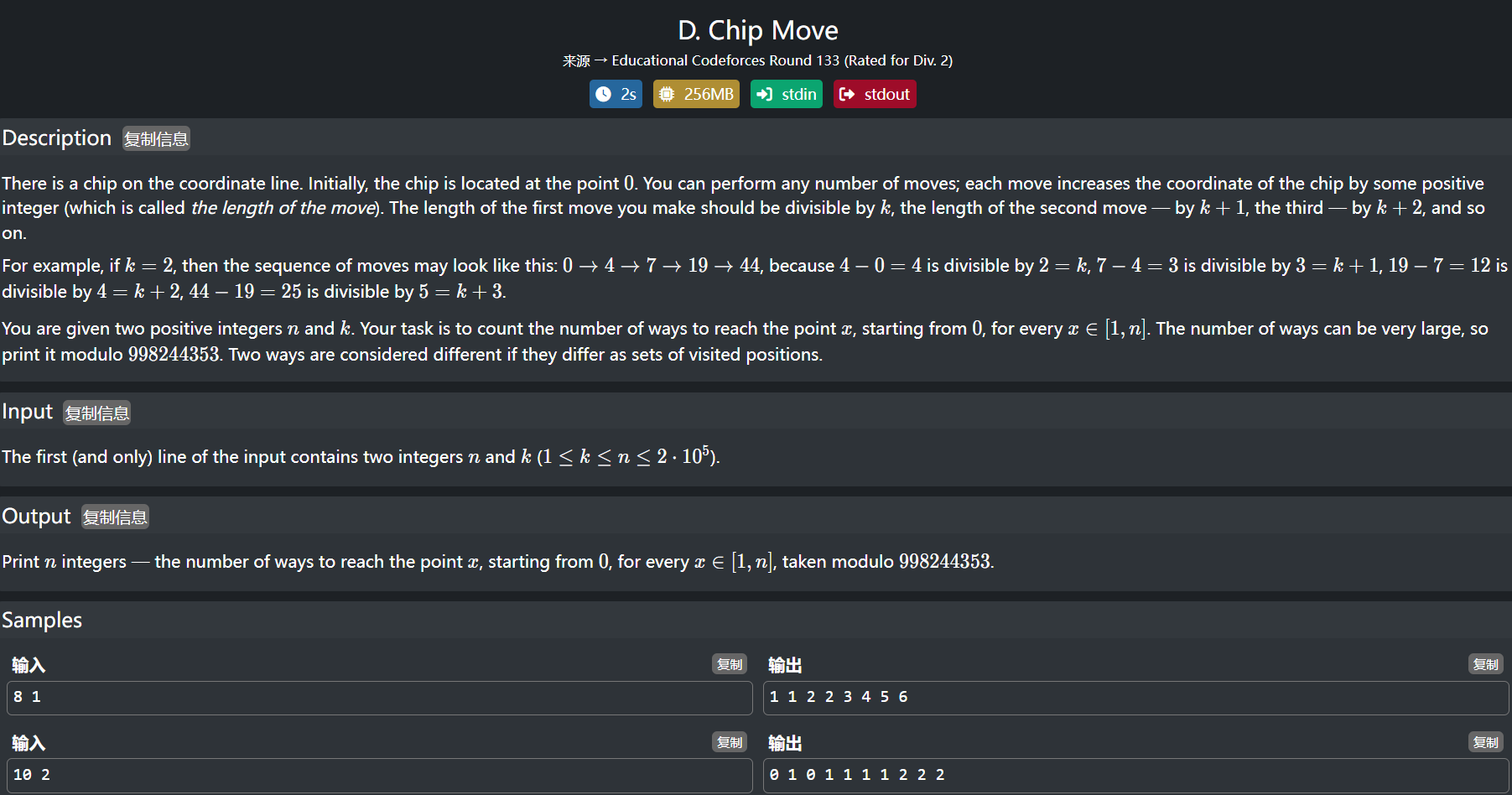
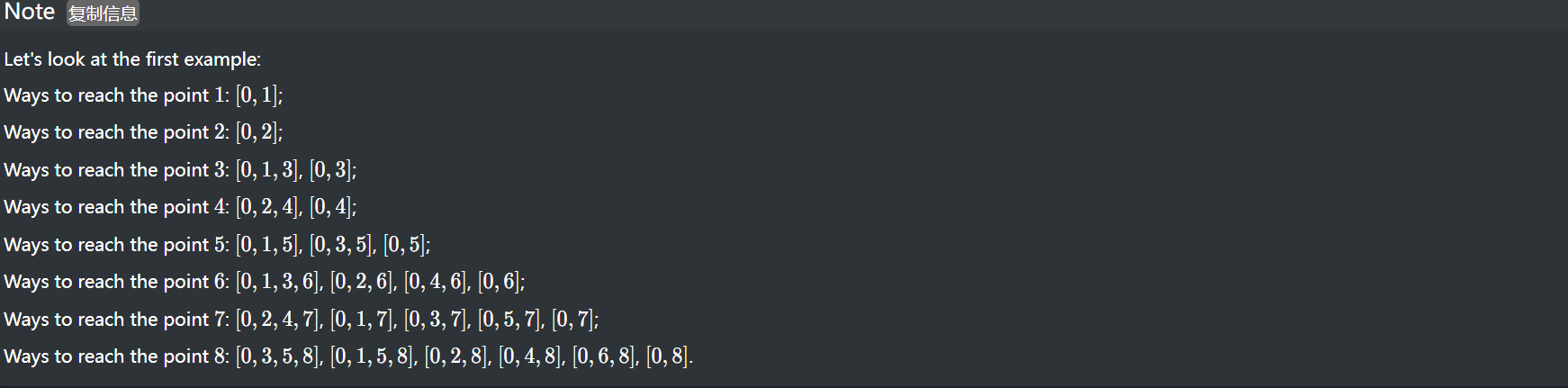
思路

根据题意，最开始可以想到一个二维的dp状态
用dp[i][j]表示跳了j次刚好到i的方案数
如果是跳了j次，那么这次应该要被k+j-1整除才行
那么这样状态转移就是
dp[i][j] = dp[i][j]+dp[i-(k+j-1)x][j-1]
(k+j-1)x表示倍数
时间复杂度是nlogn根号n,但是这样做不仅空间复杂度超限，并且时间也会超时

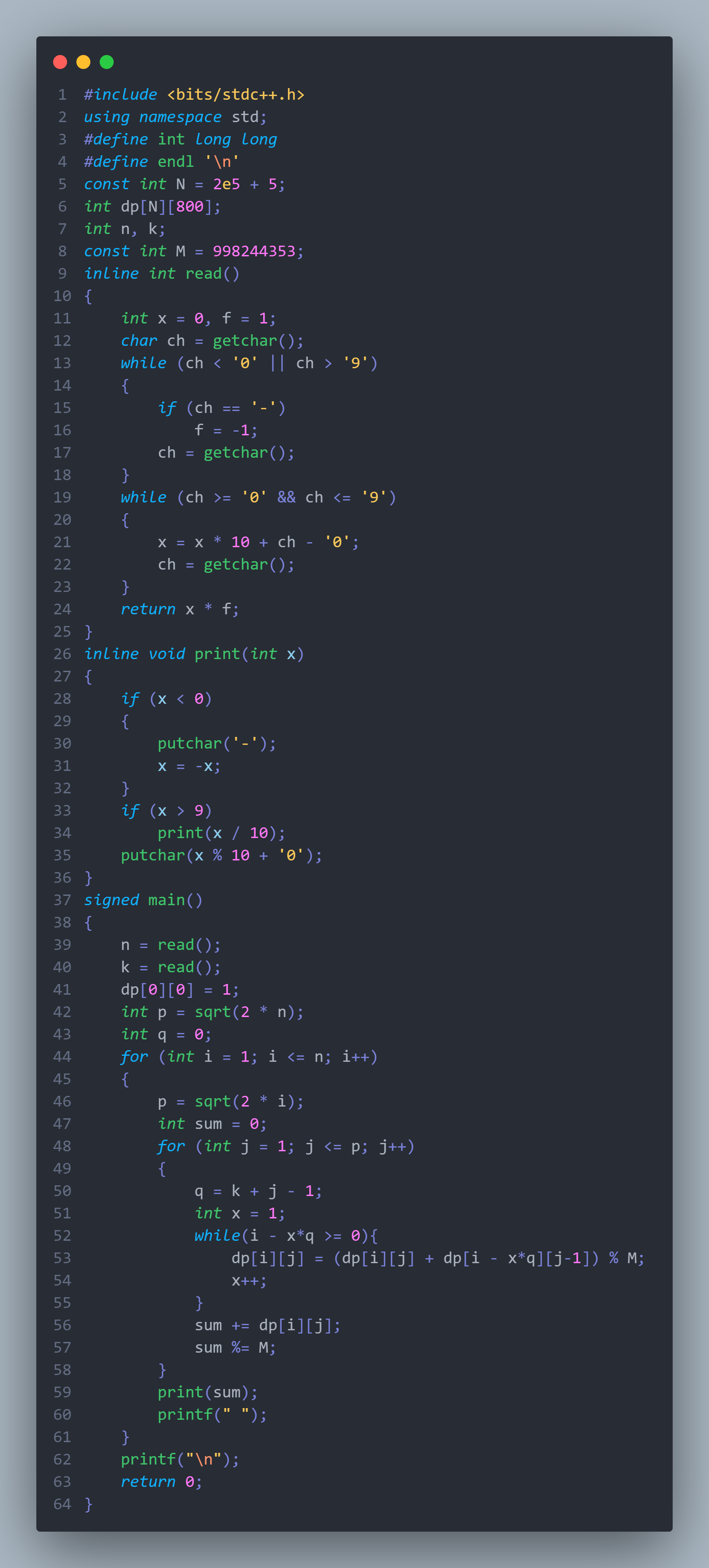
所以考虑如何去优化化此状态
我们发现每次跳j次都由j-1次转移而来，所以应该把第二维状态优化掉
这样dp[i]表示循环到j次时，能到i的方案数
考虑使用完全背包解决，但是这样做会出现一些问题，因为题目中要求每一次都必须要跳

for(int j = p; j <= n; j++){
            dp[j] += dp[j-p];
            dp[j] %= M;
    }

所以我们在刚开始要排除没有跳的情况
利用递推的方式，如果跳了j次的方案数都是正确转移的
那么第j+1次如果是被step整除
上一次从n~step 的方案数应该都和n-step~0等价（如果上一次正确转移，那么这一次直接跳step步不超过n就行）
而跳j+1次显然都是到不了0~step-1的（第j+1次必须跳step的整数倍），所以都置为0

代码

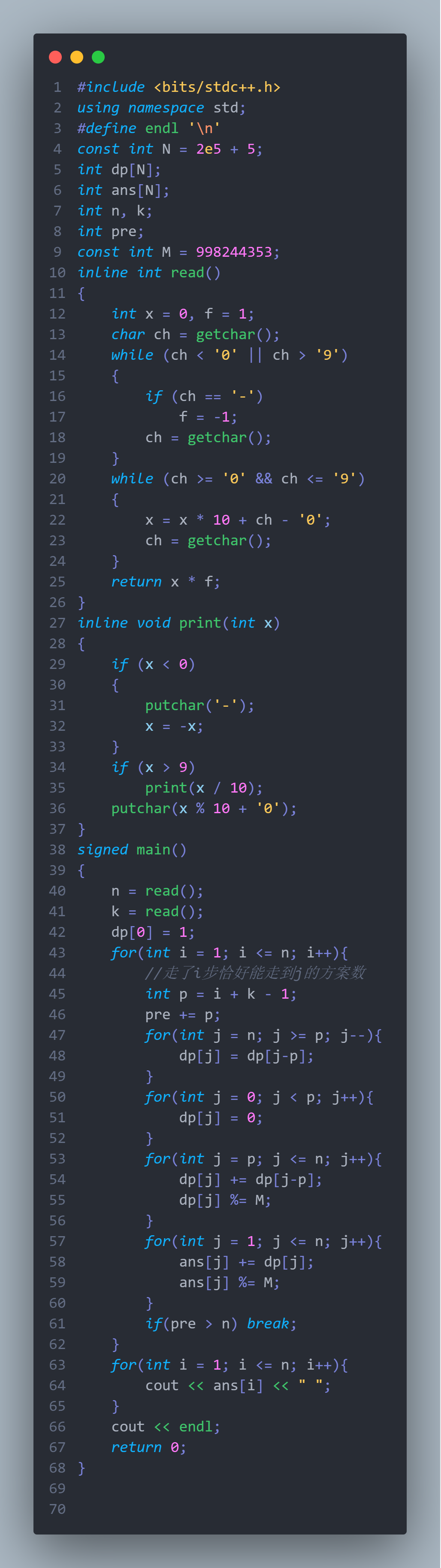
可复制版

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N = 2e5 + 5;
int dp[N];
int ans[N];
int n, k;
int pre;
const int M = 998244353;
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(int x)
{
    if (x < 0)
    {
        putchar('-');
        x = -x;
    }
    if (x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
signed main()
{
    n = read();
    k = read();
    dp[0] = 1;
    for(int i = 1; i <= n; i++){
        //走了i步恰好能走到j的方案数
        int p = i + k - 1;
        pre += p;
        for(int j = n; j >= p; j--){
            dp[j] = dp[j-p];
        }
        for(int j = 0; j < p; j++){
            dp[j] = 0;
        }
        for(int j = p; j <= n; j++){
            dp[j] += dp[j-p];
            dp[j] %= M;
        }
        for(int j = 1; j <= n; j++){
            ans[j] += dp[j];
            ans[j] %= M;
        }
        if(pre > n) break;
    }
    for(int i = 1; i <= n; i++){
        cout << ans[i] << " ";
    }
    cout << endl;
    return 0;
}