快速排序和希尔排序
背景：复习使用
快速排序
思想和时间复杂度
快速排序是由东尼·霍尔所发展的一种排序算法。
在平均状况下，排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较，但这种状况并不常见。
快速排序又是一种分而治之思想在排序算法上的典型应用。
虽然 Worst Case 的时间复杂度达到了 O(n²)，但是在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好。
快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。 ------《算法艺术和信息学奥赛》
由于基准值的不确定，快速排序经常要交换两个数的相对位置，所以快速排序不是稳定的排序算法
可以说，快速排序是优化版的冒泡排序
算法步骤
- 从数列中挑出一个元素，称为 "基准"（pivot）;
- 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
- 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
代码实现
Paritition1(int A[], int low, int high) {
int pivot = A[low];//基准初始值从low开始
while (low < high) {
while (low < high && A[high] >= pivot) {
--high;
}
A[low] = A[high];//找到high起第一个比基准值小的元素
while (low < high && A[low] <= pivot) {
++low;
}
A[high] = A[low];//找到low起第一个比基准值大的元素
}
A[low] = pivot;//还原基准值
//由于是递归实现，此时已经按照基准值分好了界限
return low;
}
void QuickSort(int A[], int low, int high) //快排母函数
{
if (low < high) {
int pivot = Paritition1(A, low, high);
QuickSort(A, low, pivot - 1);
QuickSort(A, pivot + 1, high);
}
}
import java.util.Scanner;
public class quicksort {
public void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
return;
}
public int Partition(int[] a, int p, int r) {
int x = a[p];// 划分元
int i = p;
int j = r + 1;
while (true) {
while (a[--j] >= x && j > p)
;
swap(a, i, j); // 交换第一个比划分元小的元素，a[j]是划分元，后面的元素都比它大
while (a[++i] <= x && i < r)
;
if (i >= j)
break;
swap(a, i, j); // 交换第一个比划分元小的元素，a[i]是划分元，前面的元素都比它小
}
return j;
}
public void quicks(int[] a, int l, int r) {
if (l < r) {
int p = Partition(a, l, r);
quicks(a, l, p - 1);
quicks(a, p + 1, r);
}
return;
}
public static void main(final String args[]) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] a = new int[n + 5];
for (int i = 1; i <= n; i++)
a[i] = scan.nextInt();
scan.close();
quicksort temp = new quicksort();
temp.quicks(a, 1, n);
for (int i = 1; i <= n; i++)
System.out.printf("%d ", a[i]);
}
}
希尔排序
思想和时间复杂度
希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。
希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。
希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
算法步骤
- 选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
- 按增量序列个数 k，对序列进行 k 趟排序；
- 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
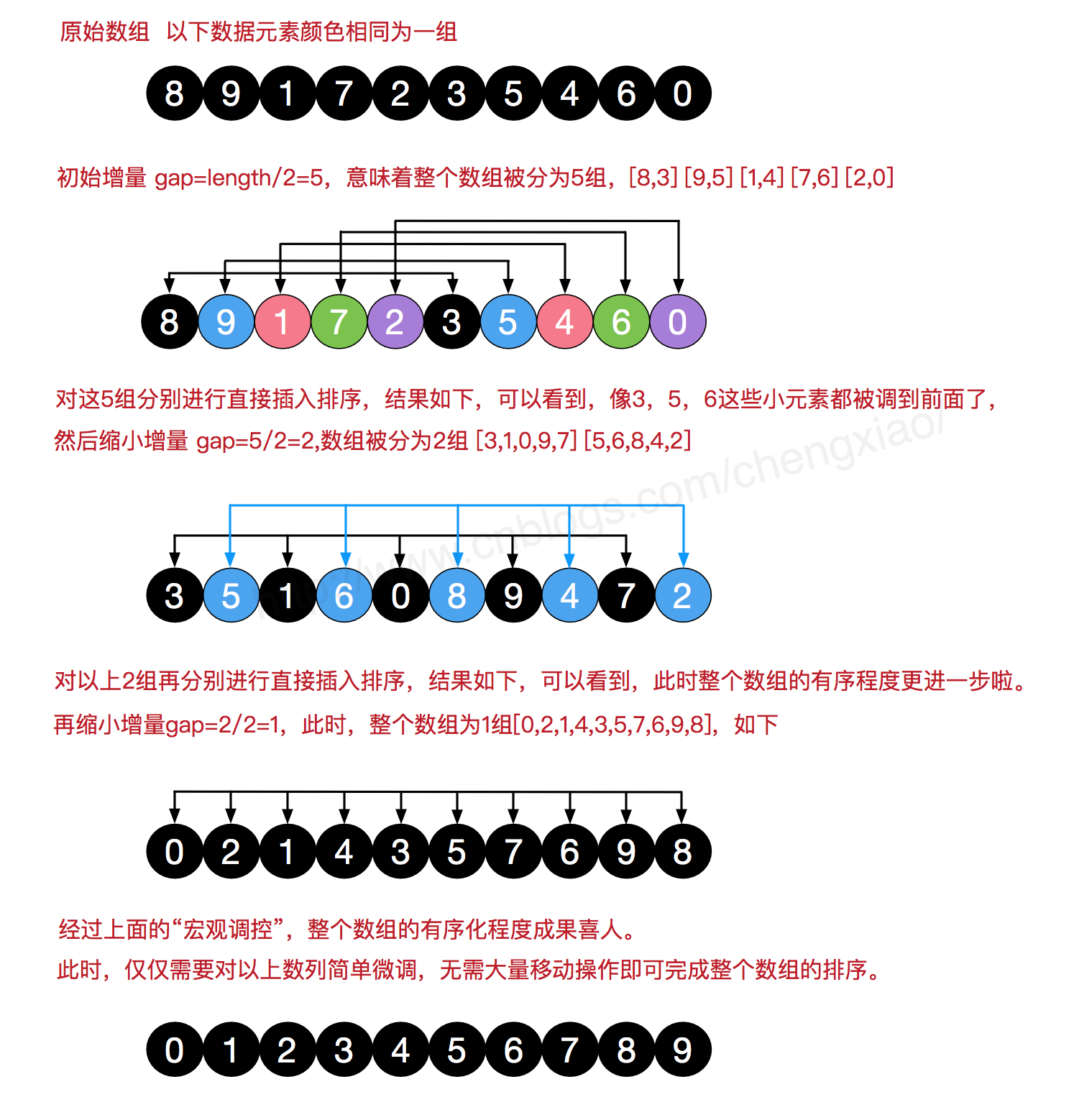图片来自网络
代码实现
void shellsort(int arr[], int n) {
int gap, i, j, temp;
for(gap = n/2; gap > 0; gap /= 2)
for(i = gap; i < n; i++)
for(j = i - gap; j >= 0 && arr[j] > arr[j+gap]; j -= gap) {
temp = arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
