Acwing 883高斯消元法的运用
Acwing 883高斯消元法的运用
解线性方程组
Acwing 883
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 m 个方程 n 个未知数的线性方程组示例:
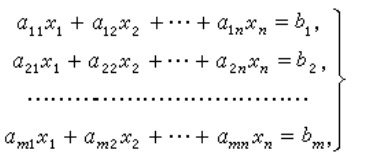
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出<Infinite group solutions>。
如果给定线性方程组无解,则输出 <No solution>。
数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例:
1.00
-2.00
3.00
Train of thought
根据线性代数高斯消元求解线性方程组的方法:
从每一列的角度考虑,先找出每一列中绝对值最大的数
然后把这个数所对应行与对应要处理的行交换,我们要做的就是尽可能地将它化为阶梯型矩阵
如:按照样例来分析
所对应的增广矩阵变化为

现在我们的任务是处理第一行,将第一行第一列归一以后把下面每行第一个数消掉
所以原矩阵变为

可以看到第一列的任务已经完成了,下面开始处理第二行,后面的思路以此类推
最后应化为上三角矩阵
Note:
- 由于最后处理完是上三角矩阵,如果是有解的,我们还要从最后一行来进行向上的消元,这样才能得到每一个元素的解
- 由于计算机浮点数的不精确度,我们需要定义一个浮点数常量来判断当前的数是否为0,在本题中可以设为1e-6
- 如果判断出当前的那一列最大的数为0;应该直接循环下一列,而待处理的行不发生改变;
- 判断无解的情况即0 = bi,而bi通过计算不为0;
综上所述,代码如下:
#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
double Matrix[105][105];
int n;
double Exp = 1e-6;
int guass()
{
int c,r;
for(c = 1,r = 1; c <= n; ++c)
{
int p = r;
for(int t = r; t <= n; ++t)
if(fabs(Matrix[t][c]) > fabs(Matrix[p][c]))
p = t;//找到绝对值最大的数所对应的行
if(fabs(Matrix[p][c]) < Exp) continue;//这里对应第三点注意
for(int i = c; i <= n + 1; ++i) swap(Matrix[p][i], Matrix[r][i]);
for(int i = n + 1; i >= c; --i) Matrix[r][i] /= Matrix[r][c];//第一个系数归一
for(int i = r + 1; i <= n; ++i)
for(int j = n + 1; j >= c; --j)
if(fabs(Matrix[i][c] )> Exp)
Matrix[i][j] -= Matrix[i][c] * Matrix[r][j];//消元
r++;
}
if(r <= n)
{
for(int i = r; i <= n; ++i)
if(fabs(Matrix[i][n + 1]) > Exp)
return 1;//对应第4点注意
return 2;
}
for (int i = n ; i >= 1; i -- )
for (int j = i - 1; j >= 1; j -- )
Matrix[j][n + 1] -= Matrix[j][i] * Matrix[i][n + 1];
return 0;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n + 1; ++j)
cin >> Matrix[i][j];
int t = guass();
cout << setprecision(2) <<fixed;
if(t == 0)
for(int i = 1; i <= n; ++i)
cout << Matrix[i][n + 1] << endl;
else if(t == 1)
cout << "No solution" << endl;
else
cout << "Infinite group solutions" << endl;
return 0;
}
感谢大家的阅读,第一次写博客,有些地方做的不好的恳请大家指出,一定会多加改进( ̄▽ ̄)



