E-Tree Xor_2021牛客暑期多校训练营4
E-Tree Xor_2021牛客暑期多校训练营4 (nowcoder.com)
题目:
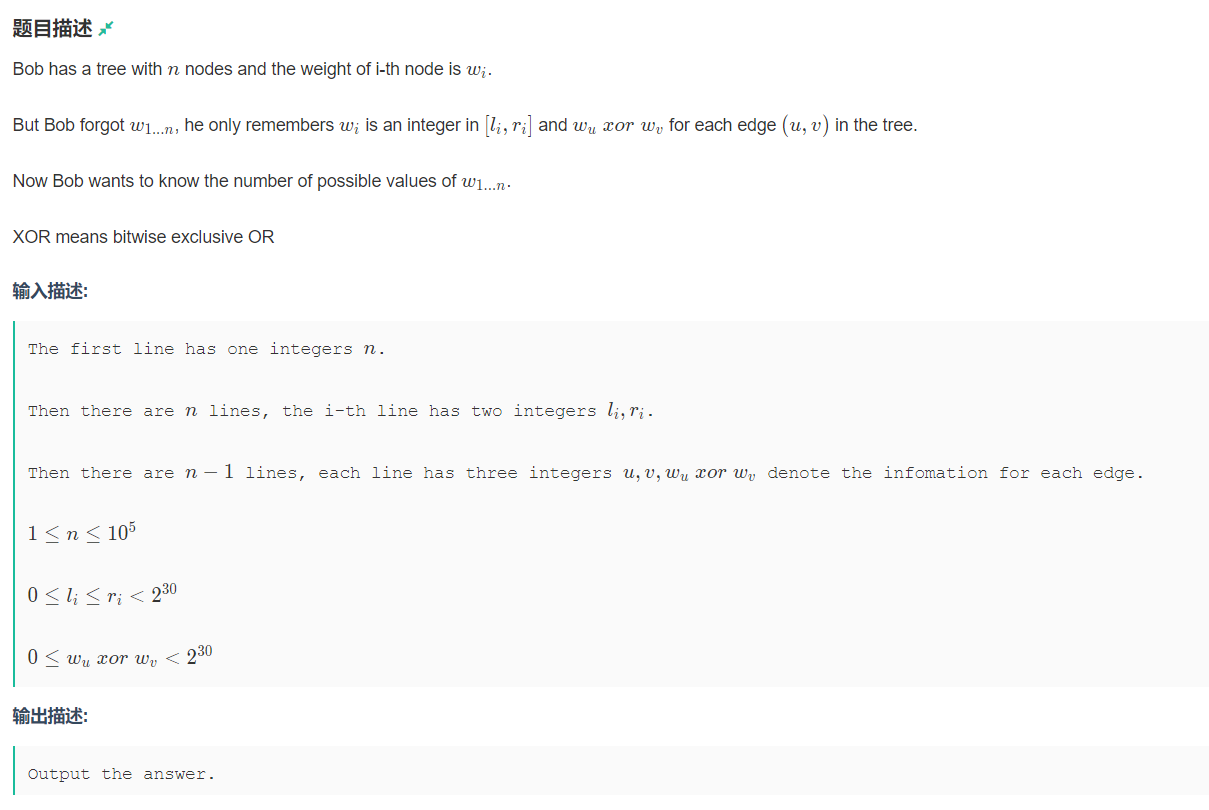
题意:
给n个点,n-1条边。每个点都有一个取值范围\([l_i,r_i]\),每条边 x->y 都有一个边权w,表示 x 点到 y 点时点值需异或上w,求最多有多少个数fx可以选择,使得fx从任意一点出发,异或上相邻节点边权都符合相邻节点取值范围。
思路:
首先,最暴力的想法就是将1设为根节点,遍历相邻节点,把相邻节点区间每一个数\(x_i\)异或上边权w,得到一堆离散的点,把这些点存起来递归子树,执行相同操作,又会得到一堆离散的点。递归结束后,统计一下每个点出现的次数,次数=n说明这个点可行,答案加1。\(10^9\)的数据量显然复杂度爆炸。
现在考虑优化,首先我们还是需要dfs一遍求出每个点需要异或的值。
问题来了,区间异或一个值会得到一堆散点,如何处理这堆散点?
例 求\([1,4]\bigoplus2\)的值, 我们会得到 [0,1,3,6],看似散了,其实不然。我们放到01字典树上看看。
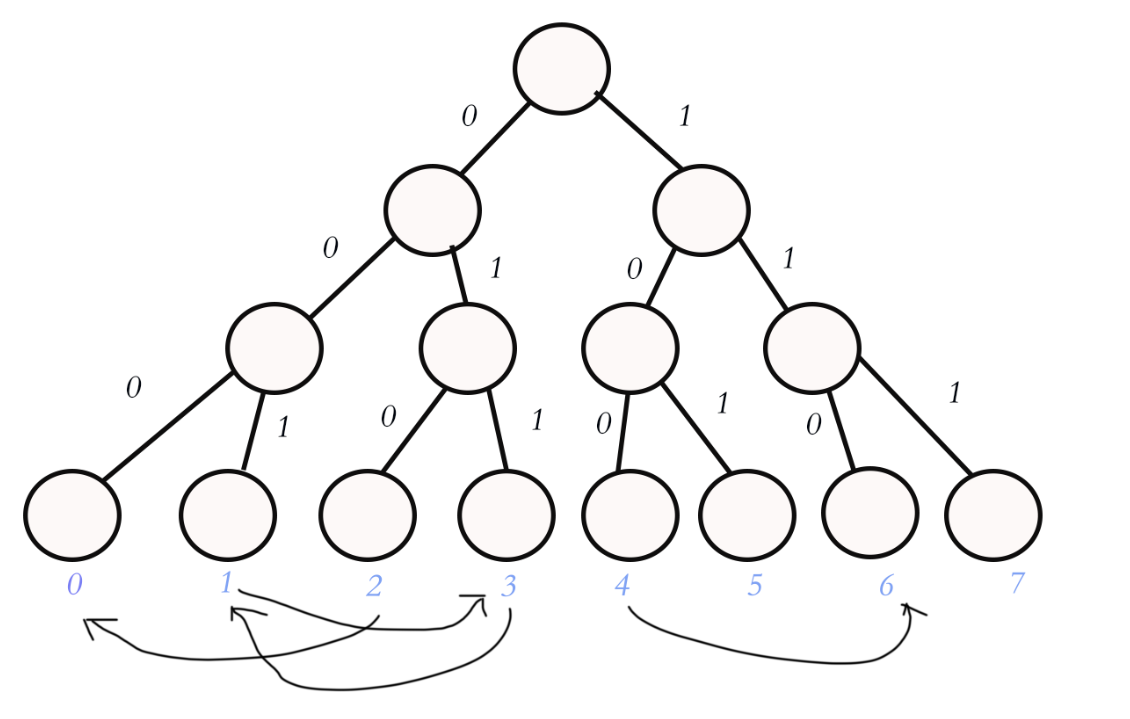
我们将2(010)从高位开始与字典树异或。
我们会观察到01字典树进行异或运算的一个性质:若当前二进制位为0,左右子树不变,若为1,则左右子树互换。
例如:我们找1(001)的时候,与2(010)进行异或运算。(看2的二进制位是否为1
第一次 \(0\bigoplus0=0\) 不变化
第二次 \(0\bigoplus1=1\) 左子树变成右子树
第三次 \(1\bigoplus0=1\) 不变化
按照变换关系放到图中刚好就是3的位置 也就是 011.
有了这个性质之后,我们会发现一个事实,若某个节点的子树节点完全属于\([l_i,r_i]\),那么这个节点一下的子树就没有必要进行异或操作了,因为异或操作只会变化左右子树,而这个节点的子树再怎么变换也都是这个结点的子树。
例:我们处理2,3时,处理到2,3共同的祖先就可以了,此时我们会得到(00?),?取值0,1得到000=0,001=1 。
有了这两个结论,我们就可以处理一些复杂的。
例: 求\([0,4]\bigoplus 5\)的
5(101)
我们先对左半边异或,\(0\bigoplus1=1\) ,左子树变右子树。
继续向下异或时发现区间包含[0,3],则不需要继续向下异或了,因为继续异或也都是此节点的子树。我们这是会得到 (1??) ?自由取 0,1 会得到一个区间[4,7]。
再对右半部分异或,最终会得到 \(4\bigoplus5=5\).
处理结束后我们会得到两个区间,这两个区间内部是连续的。
那么这时我们处理一段区间的时候,按照线段树的思想划分区间,若一个节点的范围完全属于区间范围,这时我们只需要将这个节点以上的高位二进制与w进行异或,节点一下的二进制位全变成0,处理完之后会得到一段区间的左端点,右端点根据节点的深度和左端点值可以记录出来。
再来看题,我们可以把一个\([l_i,r_i]\)区间分成若干个内部连续且不相交的区间。处理完n个之后,若一个区间出现了n次,那么答案就加上这段区间的长度。具体实现看代码注释。
#include<bits/stdc++.h>
#define mk make_pair
#define PII pair<int,int>
#define pb push_back
using namespace std;
int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
const int qs=1e5+7;
int n,w[qs],l[qs],r[qs];
struct node{
int nx,val;
node(){}
node(int nx,int val):nx(nx),val(val){};
};
vector<node> v[qs];
map< int ,int> mp;
map< int ,int>::iterator it;
void dfs(int x,int fa){
for(int i=0;i<v[x].size();++i){
int fx=v[x][i].nx,fv=v[x][i].val;
if(fx==fa) continue;
w[fx]=w[x]^fv;
dfs(fx,x);
}
}
void updata(int L,int R,int l,int r,int val,int pos){
if(l<=L&&r>=R){
//区间完全包含
//fl就是处理完后新的区间左端点
int fl=(L^val)&(((1<<30)-1)^((1<<pos)-1));
// fr=fl+区间数量
int fr=fl+(1<<pos)-1;
mp[fl]++; //记录新的区间左右端点
mp[fr+1]--;
return;
}
int mid=(L+R)/2;
//递归找区间 线段数思想
if(l<=mid) updata(L,mid,l,r,val,pos-1);
if(r>mid) updata(mid+1,R,l,r,val,pos-1);
}
void work(){
int ans=0;
int cnt=0,flag=0;
for(it=mp.begin();it!=mp.end();++it){
int fx=it->first; int fy=it->second;
cnt+=fy;
if(flag) ans+=fx-flag,flag=0;
//若左端点出现了n次,说明这段区间一定可行
if(cnt>=n) flag=fx;
}
printf("%d\n",ans);
}
int main(){
n=read();
for(int i=1;i<=n;++i) l[i]=read(),r[i]=read();
for(int i=1;i<n;++i){
int x,y,z;
x=read(),y=read(),z=read();
v[x].pb(node(y,z));
v[y].pb(node(x,z));
}
w[1]=0; //将1的异或值设为0
dfs(1,0); //递归得到各点异或值
mp[l[1]]++; //记录左右端点
mp[r[1]+1]--;
for(int i=2;i<=n;++i){ //处理各个区间
updata(0,(1<<30)-1,l[i],r[i],w[i],30);
}
work();
return 0;
}
蜜汁操作,同样的代码概率超时,真就随机ac呗,最快905ms。


