SDUT 2022 Summer Individual Contest - 9 (补题)
题目链接:
题意:
给定一个数组,找出第一个比q[i]大的数q[j]记录数据输出
分析:
对于一个任意的q[i]来说,若i<j且q[i]<q[j]那么答案一定不会在j后面出现,若i<j且q[i]>q[j]答案也不会在j后小于q[j]的元素中出现,所以对于每个元素可以删除其后面的元素,使用栈倒序操作即可
#include <bits/stdc++.h> #define endl '\n' #define x first #define y second #define int long long #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=1e5+10; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int q[N]; int ans[N]; void solve() { int n; cin >> n; stack<int> s; for(int i=1;i<=n;i++)cin >> q[i]; for(int i=n;i>0;i--){ if(!s.size()){ ans[i]=-1; s.push(q[i]); continue; } while (s.size()&&q[i]>=s.top()) s.pop(); if (s.size()) ans[i]=s.top(); else ans[i]=-1; s.push(q[i]); } for(int i=1;i<=n;i++)cout << ans[i] << ' '; } signed main() { SugarT int T=1; //cin >> T; while(T--) solve(); return 0; }
题目链接:
题意:
去m个超市买东西,在每个超市买东西的概率都为p,并且最多只能买一件。求在第n个超市刚好买第k个商品的概率
分析:
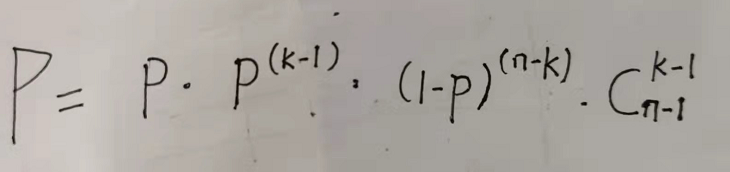
将p换成A/B A=p*10000,B=10000;
组合数利用逆元求解,最后公式为:
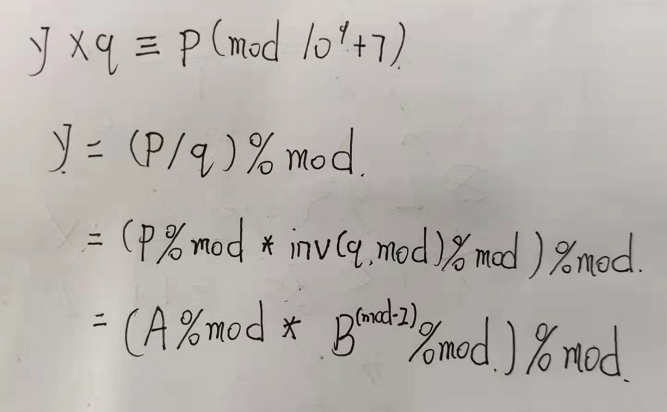
#include <bits/stdc++.h> #define endl '\n' #define x first #define y second #define int long long #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=1e5+10; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int m,n,k; int fac[N],infac[N]; double p; int gcd(int a,int b){ return b?gcd(b,a%b):a; } int qsm(int a,int b){ int res=1%mod; while(b){ if(b&1)res=res*a%mod; a=a*a%mod; b>>=1; } return res; } void init(){ fac[0]=infac[0]=1; for(int i=1;i<=N;i++) { fac[i]=fac[i-1]*i%mod; infac[i]=infac[i-1]*qsm(i,mod-2)%mod; } } int C(int n,int k){ return fac[n]*infac[k]%mod*infac[n-k]%mod; } void solve() { cin >> m >> n >> k >> p; if(k>n || n>m){ cout << "0" << endl; return; } int A=p*10000LL+eps; int B=10000LL; int kk=gcd(A,B); A/=kk,B/=kk; A=C(n-1,k-1)%mod*qsm(A,k)%mod*qsm((B-A),(n-k))%mod; B=qsm(B,n)%mod; //cout << A << " " << B << endl; cout << A*qsm(B,mod-2)%mod << endl; } signed main() { SugarT init(); int T=1; //cin >> T; while(T--) solve(); return 0; }
题目链接:
题意:
把一个字符串分成若干段,每一段里面的字符不能重复,问有多少种分法
分析:
DP
定义dp 表示字符串前n个字母的分法种数,先预处理字符串,对于每个字符,计算出以这个字符为结尾的无重复字符的一段最长的长度,第i个字符对应的长度记为f[i]:
dp[0]=1;dp[i]=dp(i-j) (1<=j<=f[i])
可以拿样例三模拟一下
#include <bits/stdc++.h> #define endl '\n' #define x first #define y second #define int long long #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=1e5+10; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int n,ans; int q[N]; int dp[N]; int cnt[N]; void solve() { cin >> n; string s; cin >> s; s=' '+s; for(int i=1;i<=n;i++)q[i]=s[i]-'0'; for(int i=1;i<=n;i++) { map<int,int> mp; mp.clear(); int flag=0; for(int j=i;j>=1;j--) { if(mp[q[j]]) { flag=j; break; } else mp[q[j]]=1; } cnt[i]=i-flag; } //for(int i=1;i<=n;i++)cout << cnt[i] << " "; dp[0]=1; for(int i=1;i<=n;i++){ int res=0; for(int j=1;j<=cnt[i];j++) res=(res+dp[i-j])%mod; dp[i]=res; } cout << dp[n]%mod << endl; } signed main() { int T=1; //cin >> T; while(T--) solve(); return 0; }
题目链接:
题意:
用1-9填满方格,每个数一次,相邻的数的位置也必须相邻
分析:
DFS进行全排列,然后进行check即可
#include <bits/stdc++.h> #define endl '\n' #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=1e5+10; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int ans; bool st[10]; int q[5][5]; vector<int> v; int dx[8]={-1,-1,-1,0,0,1,1,1}; int dy[8]={-1,0,1,-1,1,-1,0,1}; void dfs(int u){ if(u==v.size()){ bool flag=true; for(int i=1;i<=3;i++) for(int j=1;j<=3;j++){ auto t=q[i][j]; if(t==9)continue; bool ok=false; for(int k=0;k<8;k++){ int x=i+dx[k],y=j+dy[k]; if(q[x][y]==t+1){ ok=true; break; } } if(!ok)flag=false; } if(flag)ans++; return; } for(int i=1;i<=9;i++){ if(!st[i]){ int x=v[u]/10; int y=v[u]%10; q[x][y]=i; st[i]=true; dfs(u+1); st[i]=false; } } } void solve() { int cnt=0; for(int i=1;i<=3;i++) for(int j=1;j<=3;j++){ int k; scanf("%1d",&k); q[i][j]=k; if(k){ cnt++; st[k]=true; } else v.push_back(i*10+j); } dfs(0); cout << ans << endl; } int main() { int T=1; //cin >> T; while(T--) solve(); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号