并不是很短的最短路

引用文献链接:
最短路题单:
最短路分类及时间复杂度:
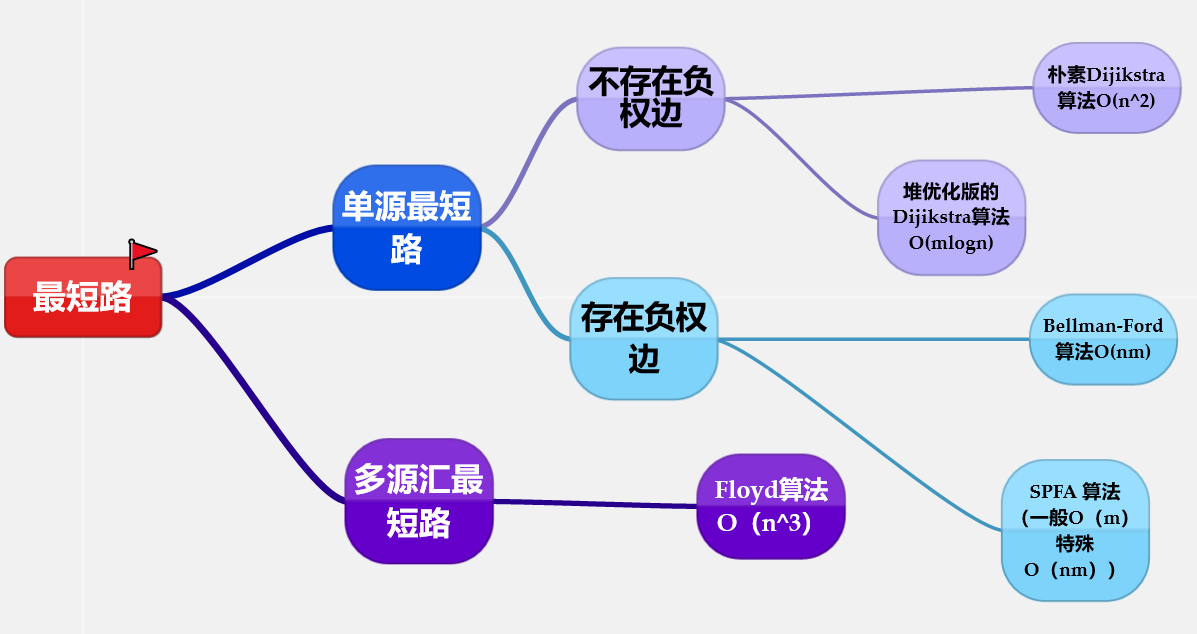
松弛操作:
以下为官方解释(非人话解释):

以下为人话解释
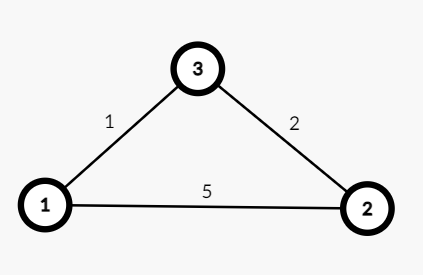
Floyd算法
是用来求任意两个结点之间的最短路的。
复杂度比较高,但是常数小,容易实现。(我会说只有三个 for 吗?)
适用于任何图,不管有向无向,边权正负,但是最短路必须存在。(不能有个负环)
三维的数组能够优化成二维数组进行计算
如图是三维数组思路及模板(摘自OI WiKi) 暴力且无脑66

题目链接:
代码实现:
#include <bits/stdc++.h> #define endl '\n' #define x first #define y second #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=210; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int n,m,k; int dist[N][N]; void Floyd() { for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);//不停的进行迭代操作 } void solve() { cin >> n >> m >> k; memset(dist,0x3f,sizeof dist); for(int i=0;i<=n;i++)dist[i][i]=0; while(m--) { int a,b,c; cin >> a >> b >> c; dist[a][b]=min(dist[a][b],c);//取出现的最小值 } Floyd(); while(k--) { int a,b; cin >> a >> b; if(dist[a][b]>0x3f3f3f3f/2) cout << "impossible" << endl; else cout << dist[a][b] << endl; } } int main() { SugarT int T=1; //cin >> T; while(T--) solve(); return 0; }
Dijkstra(朴素)


演示数据:

1 2 1 1 3 4 2 3 2 3 5 1 2 5 5 5 6 6 5 4 3 2 4 7 4 6 2
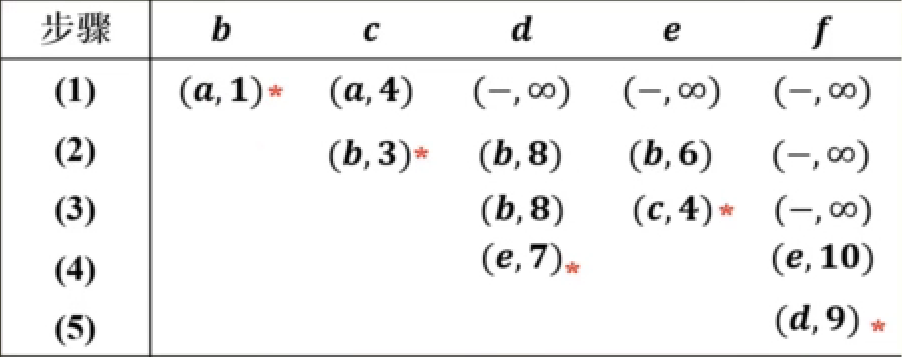
题目链接:
代码实现:
#include <bits/stdc++.h> #define endl '\n' #define x first #define y second #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=510; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int n,m; int g[N][N]; int dist[N]; bool st[N]; void Dijkstra() { memset(dist,0x3f,sizeof dist); dist[1]=0; for(int i=0;i<n-1;i++) { int t=-1; for(int j=1;j<=n;j++) if(!st[j] && (t==-1 || dist[t]>dist[j])) t=j; st[t]=true; for(int j=1;j<=n;j++) dist[j]=min(dist[j],dist[t]+g[t][j]); } printf("%d\n",dist[n]>INF/2?-1:dist[n]); } void solve() { memset(g,0x3f,sizeof g); cin >> n >> m; while(m--) { int a,b,c; cin >> a >> b >> c; g[a][b]=min(g[a][b],c); } Dijkstra(); } int main() { SugarT int T=1; //cin >> T; while(T--) solve(); return 0; }
Dijkstra(堆优化)
题目链接:
代码实现:
#include <bits/stdc++.h> #define endl '\n' #define x first #define y second #define PI acos(-1) #define SugarT ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; typedef long long LL; typedef unsigned long long ULL; typedef pair<int,int> PII; const int N=1e6+10; const int M=510; const int INF=0x3f3f3f3f; const int mod=1e9+7; const double eps = 1e-6; int n,m; int h[N],e[N],ne[N],w[N],idx; int dist[N]; bool st[N]; void add(int a,int b,int c) { e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++; } void Dijkstra() { memset(dist,0x3f,sizeof dist); dist[1]=0; priority_queue<PII,vector<PII>,greater<PII>> q; q.push({0,1}); while(q.size()) { auto t=q.top(); q.pop(); int dis=t.x,ver=t.y; if(st[ver])continue; st[ver]=true; for(int i=h[ver];i!=-1;i=ne[i]) { auto j=e[i]; if(dist[j]>dist[ver]+w[i]) { dist[j]=dist[ver]+w[i]; q.push({dist[j],j}); } } } printf("%d\n",dist[n]>INF/2?-1:dist[n]); } void solve() { memset(h,-1,sizeof h); cin >> n >> m; while(m--) { int a,b,c; cin >> a >> b >> c; add(a,b,c); } Dijkstra(); } int main() { SugarT int T=1; //cin >> T; while(T--) solve(); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号