整除分块

给定一段连续的区间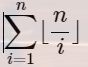中n/i（下取整）的值是不会发生变化的

 

 

[4,5]  [6,10]

对于这些相似的n/i只要计算出他们的区间左右端点各是多少

就可以用O（1）的时间复杂度求解这一部分了

小知识

 

所以下面的题目如果求区间内n%i的最大值也就是n-i*[n/i]的最大值

我们用整除分块的思想计算出一定数量（k^1/2）的区间内[n/i]值相等，然后公式前面的n相等

所以能得到区间内的左端点满足max（l）=max（l,r）

即左端点即为最大值

 

 

 

 

#include <bits/stdc++.h>
#define endl '\n'
#define x first
#define y second
#define int long long
#define Tang ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);

using namespace std;

const int N=1e5+10;
const int INF=0x3f3f3f3f;
const int mod=1e9+7;

void solve()
{
    
    int n,m;
    cin >> n >> m;
    while(m--)
    {
        int ans=0;
        int L,R;
        cin >> L >> R;
        for(int l=L,r;l<=R;l=r+1)
        {
            r=min(n/(n/l),R);
            ans=max(ans,n%l);
        }
        cout << ans << endl;
    }
    
}

signed main()
{
    Tang
    int T=1;
        //cin >> T;
    while(T--)
        solve();
    
    return 0;
        
}