决策树基础梳理
1.信息论基础
1.1.熵
熵是信息的关键度量,通常指一条信息中需要传输或者存储一个信号的平均比特数。熵衡量了预测随机变量的不确定度,不确定性越大熵越大。
针对随机变量XX,其信息熵的定义如下:
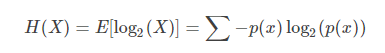
信息熵是信源编码中,压缩率的下限。当我们使用少于信息熵的信息量做编码,那么一定有信息的损失。
1.2.联合熵
联合熵是一集变量之间不确定的衡量手段。
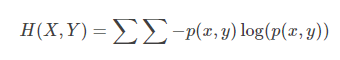
1.3.条件熵
条件熵描述变量Y在变量X确定的情况下,变量Y的熵还剩多少。

联合熵和条件熵的关系是:
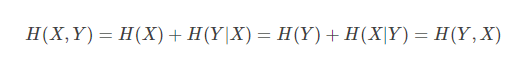
1.4.信息增益
信息增益在决策树算法中是用来选择特征的指标,信息增益越大,则这个特征的选择性越好,在概率中定义为:待分类的集合的熵和选定某个特征的条件熵之差(这里只的是经验熵或经验条件熵,由于真正的熵并不知道,是根据样本计算出来的),公式如下:
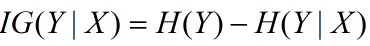
1.5.基尼不纯度
基尼不纯度:将来自集合的某种结果随机应用于某一数据项的预期误差率。
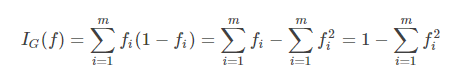
- (1)显然基尼不纯度越小,纯度越高,集合的有序程度越高,分类的效果越好;
- (2)基尼不纯度为 0 时,表示集合类别一致;
- (3)基尼不纯度最高(纯度最低)时,
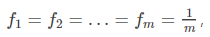
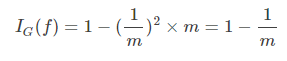
2.ID3算法
2.1原理
ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征,递归地构建决策树。具体方法是:从根结点开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点;再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树,ID3相当于用极大似然法进行概率模型的选择
2.2过程
1.决策树开始时,作为一个单个节点(根节点)包含所有训练样本集
2.若一个节点的样本均为同一类别,则该节点就成为叶节点并标记为该类别。否则算法将采用信息熵(成为信息增益)作为启发指示来帮助选择合适的(分支)属性,以便将样本集划分为若干自己。选择能够最好地讲样本分类的属性。该属性成为该节点的“测试”或“判定”属性。在算法中,所有属性均为离散值,若有取连续值的属性,必须首先将其离散化。
3.对测试属性的每个已知的值,创建一个分支,并据此划分样本
4.算法使用同样的过程,递归的形成每个划分上的样本判定树。一旦一个属性出现在一个节点上,就不必考虑该节点的任何后代
递归划分步骤仅当下列条件之一成立时立即停止:
1.给定节点的所有样本属于同一类
2.没有剩余属性可以用来进一步划分样本。在此情况下,使用多数表决,讲给定的节点转换成树叶,并用样本中的多数所在的类标记它。另外,可以存放节点样本的类分布。
3.分支test_attribute=a(i),没有样本。在这种情况下,以samples中的多数类创建一个树叶。
2.3优缺点
优点:
理论清晰,算法简单,很有实用价值的示例学习算法;
计算时间是例子个数、特征属性个数、节点个数之积的线性函数,总预测准确率较令人满意
缺点:
存在偏向问题,各特征属性的取值个数会影响互信息量的大小;
特征属性间的相关性强调不够,是单变元算法;
对噪声较为敏感,训练数据的轻微错误会导致结果的不同;鲁棒性
结果随训练集记录个数的改变而不同,不便于进行渐进学习
3.C4.5
3.1原理
C4.5算法是用于生成决策树的一种经典算法,是ID3算法的一种延伸和优化。
C4.5算法采用PEP(Pessimistic Error Pruning)剪枝法
C4.5算法通过信息增益率选择分裂属性。
属性A的“分裂信息”(split information):、

其中,训练数据集S通过属性A的属性值划分为m个子数据集,|Sj||Sj|表示第j个子数据集中样本数量,|S||S|表示划分之前数据集中样本总数量。
通过属性A分裂之后样本集的信息增益:
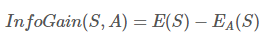
通过属性A分裂之后样本集的信息增益率:
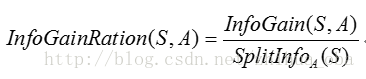
通过C4.5算法构造决策树时,信息增益率最大的属性即为当前节点的分裂属性,随着递归计算,被计算的属性的信息增益率会变得越来越小,到后期则选择相对比较大的信息增益率的属性作为分裂属性。
3.2过程
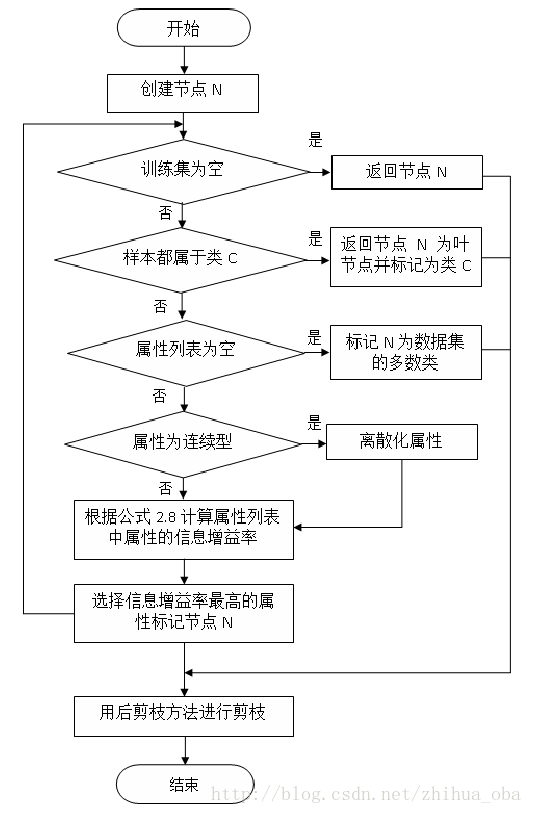
3.3优缺点
优点:
(1)通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
(2)能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
(3)构造决策树之后进行剪枝操作;
(4)能够处理具有缺失属性值的训练数据。
缺点:
(1)算法的计算效率较低,特别是针对含有连续属性值的训练样本时表现的尤为突出。
(2)算法在选择分裂属性时没有考虑到条件属性间的相关性,只计算数据集中每一个条件属性与决策属性之间的期望信息,有可能影响到属性选择的正确性。
4.CART分类树
4.1原理
Classification And Regression Tree(CART)是决策树的一种,并且是非常重要的决策树,属于Top Ten Machine Learning Algorithm。顾名思义,CART算法既可以用于创建分类树(Classification Tree),也可以用于创建回归树(Regression Tree)、模型树(Model Tree),两者在建树的过程稍有差异。前文“机器学习经典算法详解及Python实现–决策树(Decision Tree)”详细介绍了分类决策树原理以及ID3、C4.5算法,本文在该文的基础上详述CART算法在决策树分类以及树回归中的应用。
创建分类树递归过程中,CART每次都选择当前数据集中具有最小Gini信息增益的特征作为结点划分决策树。ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但其生成的决策树分支、规模较大,CART算法的二分法可以简化决策树的规模,提高生成决策树的效率。对于连续特征,CART也是采取和C4.5同样的方法处理。为了避免过拟合(Overfitting),CART决策树需要剪枝。预测过程当然也就十分简单,根据产生的决策树模型,延伸匹配特征值到最后的叶子节点即得到预测的类别。
创建回归树时,观察值取值是连续的、没有分类标签,只有根据观察数据得出的值来创建一个预测的规则。在这种情况下,Classification Tree的最优划分规则就无能为力,CART则使用最小剩余方差(Squared Residuals Minimization)来决定Regression Tree的最优划分,该划分准则是期望划分之后的子树误差方差最小。创建模型树,每个叶子节点则是一个机器学习模型,如线性回归模型
CART算法的重要基础包含以下三个方面:
(1)二分(Binary Split):在每次判断过程中,都是对观察变量进行二分。
CART算法采用一种二分递归分割的技术,算法总是将当前样本集分割为两个子样本集,使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。因此CART算法适用于样本特征的取值为是或非的场景,对于连续特征的处理则与C4.5算法相似。
(2)单变量分割(Split Based on One Variable):每次最优划分都是针对单个变量。
(3)剪枝策略:CART算法的关键点,也是整个Tree-Based算法的关键步骤。
剪枝过程特别重要,所以在最优决策树生成过程中占有重要地位。有研究表明,剪枝过程的重要性要比树生成过程更为重要,对于不同的划分标准生成的最大树(Maximum Tree),在剪枝之后都能够保留最重要的属性划分,差别不大。反而是剪枝方法对于最优树的生成更为关键。
4.2过程
CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,左分支是取值为“是”的分支,右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征,将输入空间即特征空间划分为有限个单元,并在这些单元上确定预测的概率分布,也就是在输入给定的条件下输出的条件概率分布。
CART算法由以下两步组成:
1.决策树生成:基于训练数据集生成决策树,生成的决策树要尽量大; 决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时损失函数最小作为剪枝的标准。
2.CART决策树的生成就是递归地构建二叉决策树的过程。CART决策树既可以用于分类也可以用于回归。本文我们仅讨论用于分类的CART。对分类树而言,CART用Gini系数最小化准则来进行特征选择,生成二叉树。 CART生成算法如下:
输入:训练数据集D,停止计算的条件:
输出:CART决策树。
根据训练数据集,从根结点开始,递归地对每个结点进行以下操作,构建二叉决策树:
设结点的训练数据集为D,计算现有特征对该数据集的Gini系数。此时,对每一个特征A,对其可能取的每个值a,根据样本点对A=a的测试为“是”或 “否”将D分割成D1和D2两部分,计算A=a时的Gini系数。
在所有可能的特征A以及它们所有可能的切分点a中,选择Gini系数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点,从现结点生成两个子结点,将训练数据集依特征分配到两个子结点中去。
对两个子结点递归地调用步骤l~2,直至满足停止条件。
生成CART决策树。
算法停止计算的条件是结点中的样本个数小于预定阈值,或样本集的Gini系数小于预定阈值(样本基本属于同一类),或者没有更多特征。
五.连续特征和离散特征处理

六.剪枝 模型评估
由于决策树的建立完全是依赖于训练样本,因此该决策树对训练样本能够产生完美的拟合效果。但这样的决策树对于测试样本来说过于庞大而复杂,可能产生较高的分类错误率。这种现象就称为过拟合。因此需要将复杂的决策树进行简化,即去掉一些节点解决过拟合问题,这个过程称为剪枝。
剪枝方法分为预剪枝和后剪枝两大类。预剪枝是在构建决策树的过程中,提前终止决策树的生长,从而避免过多的节点产生。预剪枝方法虽然简单但实用性不强,因为很难精确的判断何时终止树的生长。后剪枝是在决策树构建完成之后,对那些置信度不达标的节点子树用叶子结点代替,该叶子结点的类标号用该节点子树中频率最高的类标记。后剪枝方法又分为两种,一类是把训练数据集分成树的生长集和剪枝集;另一类算法则是使用同一数据集进行决策树生长和剪枝。常见的后剪枝方法有CCP(Cost Complexity Pruning)、REP(Reduced Error Pruning)、PEP(Pessimistic Error Pruning)、MEP(Minimum Error Pruning)。
PEP(Pessimistic Error Pruning)剪枝法
PEP剪枝法由Quinlan提出,是一种自上而下的剪枝法,根据剪枝前后的错误率来判定是否进行子树的修剪,因此不需要单独的剪枝数据集。
对于一个叶子节点,它覆盖了n个样本,其中有e个错误,那么该叶子节点的错误率为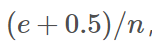 其中0.5为惩罚因子(惩罚因子一般取值为0.5)。
其中0.5为惩罚因子(惩罚因子一般取值为0.5)。
对于一棵子树,它有L个叶子节点,那么该子树的误判率为:

其中,ei表示子树第i个叶子节点错误分类的样本数量,ni表示表示子树第i个叶子节点中样本的总数量。
假设一棵子树错误分类一个样本取值为1,正确分类一个样本取值为0,那么子树的误判次数可以认为是一个伯努利分布,因此可以得到该子树误判次数的均值和标准差:
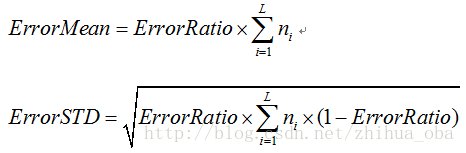
把子树替换成叶子节点后,该叶子节点的误判率为:
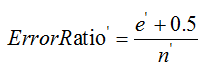
其中,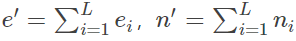
同时,该叶子结点的误判次数也是一个伯努利分布,因此该叶子节点误判次数的均值为:
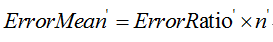
剪枝的条件为:

满足剪枝条件时,则将所得叶子节点替换该子树,即为剪枝操作。
CCP(代价复杂度)剪枝法
代价复杂度选择节点表面误差率增益值最小的非叶子节点,删除该非叶子节点的左右子节点,若有多个非叶子节点的表面误差率增益值相同小,则选择非叶子节点中子节点数最多的非叶子节点进行剪枝。
可描述如下:
令决策树的非叶子节点为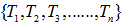 。
。
a)计算所有非叶子节点的表面误差率增益值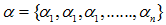
b)选择表面误差率增益值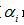 最小的非叶子节点
最小的非叶子节点 (若多个非叶子节点具有相同小的表面误差率增益值,选择节点数最多的非叶子节点)。
(若多个非叶子节点具有相同小的表面误差率增益值,选择节点数最多的非叶子节点)。
c)对 进行剪枝
进行剪枝
表面误差率增益值的计算公式:
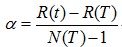
其中:
 表示叶子节点的误差代价,
表示叶子节点的误差代价,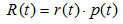 ,
,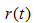 为节点的错误率,
为节点的错误率, 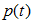 为节点数据量的占比;
为节点数据量的占比;
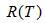 表示子树的误差代价,
表示子树的误差代价,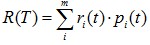 ,
, 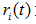 为子节点i的错误率,
为子节点i的错误率,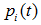 表示节点i的数据节点占比;
表示节点i的数据节点占比;
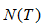 表示子树节点个数。
表示子树节点个数。
算例:
下图是其中一颗子树,设决策树的总数据量为40。
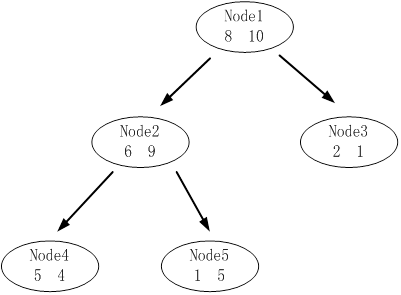
该子树的表面误差率增益值可以计算如下:
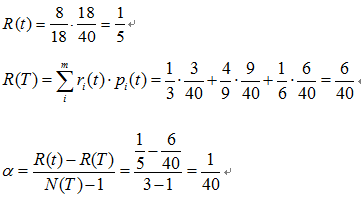
求出该子树的表面错误覆盖率为 ,只要求出其他子树的表面误差率增益值就可以对决策树进行剪枝。
七.sklearn参数详解
https://blog.csdn.net/young_gy/article/details/69666014
https://blog.csdn.net/u014688145/article/details/53212112
https://blog.csdn.net/yjt13/article/details/72794557
https://blog.csdn.net/zhihua_oba/article/details/70632622
https://blog.csdn.net/e15273/article/details/79648502



