CF# 334 Moodular Arithmetic

B. Moodular Arithmetic
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

As behooves any intelligent schoolboy, Kevin Sun is studying psycowlogy, cowculus, and cryptcowgraphy at the Bovinia State University (BGU) under Farmer Ivan. During his Mathematics of Olympiads (MoO) class, Kevin was confronted with a weird functional equation and needs your help. For two fixed integers k and p, where p is an odd prime number, the functional equation states that

for some function 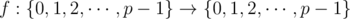. (This equation should hold for any integer x in the range 0 top - 1, inclusive.)

It turns out that f can actually be many different functions. Instead of finding a solution, Kevin wants you to count the number of distinct functions f that satisfy this equation. Since the answer may be very large, you should print your result modulo 109 + 7.

Input

The input consists of two space-separated integers p and k (3 ≤ p ≤ 1 000 000, 0 ≤ k ≤ p - 1) on a single line. It is guaranteed that p is an odd prime number.

Output

Print a single integer, the number of distinct functions f modulo 109 + 7.

Sample test(s)
input
3 2
output
3
input
5 4
output
25
Note

In the first sample, p = 3 and k = 2. The following functions work:

  1. f(0) = 0, f(1) = 1, f(2) = 2.
  2. f(0) = 0, f(1) = 2, f(2) = 1.
  3. f(0) = f(1) = f(2) = 0.

 

 

题意：给出p，k，问满足f(kx % p) = k*f(x) % p，其中0 <= f(i) < p的映射有多少种。

分析：显然f(0) = 0

考虑其他的，

如果我们确定了一个f(i)，我们会通过f(i)确定很多的映射，比如f(ki % p), f(k^2 i % p).....

什么时候会停下来？

当k^t = 1 (mod p)时会停下来。

那么就是说我们每确定一个数，就有t个数确定了。

这里的t可以通过枚举算出。

就是说我们一共只能确定(p-1)/t个数，每个数有p种可能。

ans=p^((p-1)/t)

 

  1 /**
  2 Create By yzx - stupidboy
  3 */
  4 #include <cstdio>
  5 #include <cstring>
  6 #include <cstdlib>
  7 #include <cmath>
  8 #include <deque>
  9 #include <vector>
 10 #include <queue>
 11 #include <iostream>
 12 #include <algorithm>
 13 #include <map>
 14 #include <set>
 15 #include <ctime>
 16 #include <iomanip>
 17 using namespace std;
 18 typedef long long LL;
 19 typedef double DB;
 20 #define MIT (2147483647)
 21 #define INF (1000000001)
 22 #define MLL (1000000000000000001LL)
 23 #define sz(x) ((int) (x).size())
 24 #define clr(x, y) memset(x, y, sizeof(x))
 25 #define puf push_front
 26 #define pub push_back
 27 #define pof pop_front
 28 #define pob pop_back
 29 #define mk make_pair
 30 
 31 inline int Getint()
 32 {
 33     int Ret = 0;
 34     char Ch = ' ';
 35     bool Flag = 0;
 36     while(!(Ch >= '0' && Ch <= '9'))
 37     {
 38         if(Ch == '-') Flag ^= 1;
 39         Ch = getchar();
 40     }
 41     while(Ch >= '0' && Ch <= '9')
 42     {
 43         Ret = Ret * 10 + Ch - '0';
 44         Ch = getchar();
 45     }
 46     return Flag ? -Ret : Ret;
 47 }
 48 
 49 int p, k;
 50 vector<int> factor;
 51 
 52 inline void Input()
 53 {
 54     scanf("%d%d", &p, &k);
 55 }
 56 
 57 inline int Power(int b, int t, int mod = 1000000007)
 58 {
 59     int ret = 1;
 60     while(t)
 61     {
 62         if(t & 1) ret = (1LL * ret * b) % mod;
 63         b = (1LL * b * b) % mod, t >>= 1;
 64     }
 65     return ret;
 66 }
 67 
 68 inline void Ext_Gcd(int a, int b, int &x, int &y)
 69 {
 70     if(b == 0) x = 1, y = 0;
 71     else
 72     {
 73         Ext_Gcd(b, a % b, x, y);
 74         int t = x;
 75         x = y;
 76         y = t - (a / b) * x;
 77     }
 78 }
 79 
 80 inline void Solve()
 81 {
 82     if(k == 0)
 83     {
 84         printf("%d\n", Power(p, p - 1));
 85         return;
 86     }
 87     
 88     if(k == 1)
 89     {
 90         printf("%d\n", Power(p, p));
 91         return;
 92     }
 93     
 94     /*int x, y;
 95     Ext_Gcd(k, p, x, y);
 96     if(y <= 0)
 97     {
 98         int t = y / k + 1;
 99         x -= t * p, y += t * k;
100     }
101     
102     int s;
103     LL t;
104     for(s = 1, t = k; ((t - x) % p + p) % p != 0; t *= k, s++) ;*/
105     
106     int t = p - 1;
107     for(int i = 1; i * i <= t; i++)
108         if(t % i == 0)
109         {
110             factor.pub(i);
111             factor.pub(t / i);
112         }
113     sort(factor.begin(), factor.end());
114     
115     int len = factor.size(), s;
116     for(int i = 0; i < len; i++)
117         if(Power(k, factor[i], p) == 1)
118         {
119             s = factor[i];
120             break;
121         }
122     
123     int ans = Power(p, (p - 1) / s);
124     printf("%d\n", ans);
125 }
126 
127 int main()
128 {
129     freopen("a.in", "r", stdin);
130     Input();
131     Solve();
132     return 0;
133 }
View Code

 

posted @ 2015-12-31 11:48  yanzx6  阅读(248)  评论(0)  编辑  收藏  举报