2015ACM/ICPC亚洲区长春站 B hdu 5528 Count a * b

Count a * b

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 211    Accepted Submission(s): 116


Problem Description
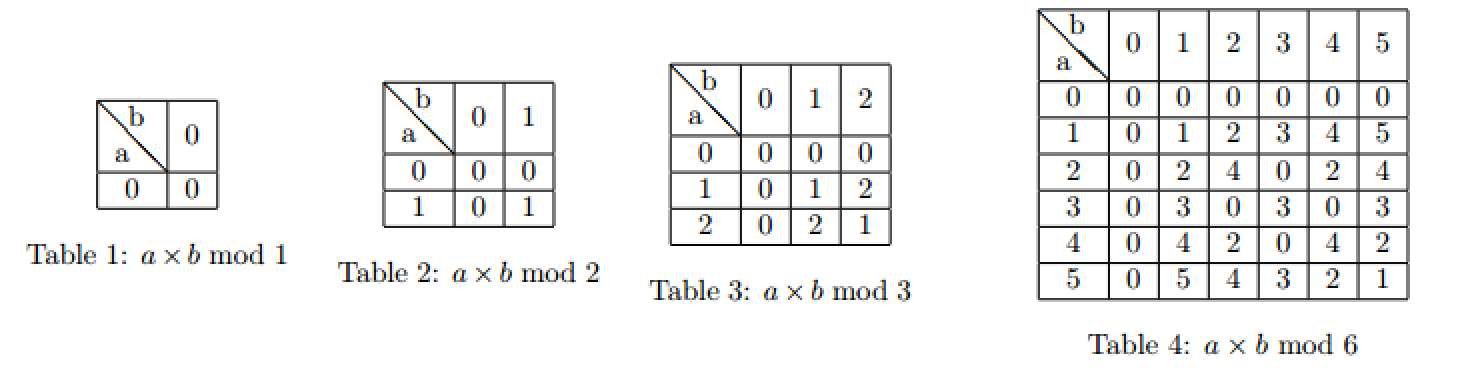
Marry likes to count the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0.

Let's denote f(m) as the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0.

She has calculated a lot of f(m) for different m, and now she is interested in another function g(n)=∑m|nf(m). For example, g(6)=f(1)+f(2)+f(3)+f(6)=0+1+4+21=26. She needs you to double check the answer.



Give you n. Your task is to find g(n) modulo 264.
 

 

Input
The first line contains an integer T indicating the total number of test cases. Each test case is a line with a positive integer n.

1≤T≤20000
1≤n≤109
 

 

Output
For each test case, print one integer s, representing g(n) modulo 264.
 

 

Sample Input
2 6 514
 

 

Sample Output
26 328194
 

 

Source
2015ACM/ICPC亚洲区长春站-重现赛（感谢东北师大）
 
题意：略
分析：http://blog.csdn.net/firstlucker/article/details/49336427
这篇题解不错。
下面说明:x的约数的欧拉函数的和 = x
即sigma(d|x, phi(d)) = x
因为对于所有1-x的数，与x的gcd必定为x的约数，设为d，那这样的数有多少？phi(x / d)个
又发现x/d也是x的约数，所以。。。
sigma(d|x, phi(d)) = sigma(d|x, phi(x/d)) = x
这篇题解最后一步用了约数和定理。
 
其代码中防溢出运算更是简单、机智的令人发指
 
  1 #include <cstdio>
  2 #include <cstring>
  3 #include <cstdlib>
  4 #include <cmath>
  5 #include <ctime>
  6 #include <iostream>
  7 #include <map>
  8 #include <set>
  9 #include <algorithm>
 10 #include <vector>
 11 #include <deque>
 12 #include <queue>
 13 #include <stack>
 14 using namespace std;
 15 typedef long long LL;
 16 typedef double DB;
 17 #define MIT (2147483647)
 18 #define MLL (1000000000000000001LL)
 19 #define INF (1000000001)
 20 #define For(i, s, t) for(int i = (s); i <= (t); i ++)
 21 #define Ford(i, s, t) for(int i = (s); i >= (t); i --)
 22 #define Rep(i, n) for(int i = (0); i < (n); i ++)
 23 #define Repn(i, n) for(int i = (n)-1; i >= (0); i --)
 24 #define mk make_pair
 25 #define ft first
 26 #define sd second
 27 #define puf push_front
 28 #define pub push_back
 29 #define pof pop_front
 30 #define pob pop_back
 31 #define sz(x) ((int) (x).size())
 32 #define clr(x, y) (memset(x, y, sizeof(x)))
 33 inline void SetIO(string Name)
 34 {
 35     string Input = Name + ".in";
 36     string Output = Name + ".out";
 37     freopen(Input.c_str(), "r", stdin);
 38     freopen(Output.c_str(), "w", stdout);
 39 }
 40 
 41 inline int Getint()
 42 {
 43     char ch = ' ';
 44     int Ret = 0;
 45     bool Flag = 0;
 46     while(!(ch >= '0' && ch <= '9'))
 47     {
 48         if(ch == '-') Flag ^= 1;
 49         ch = getchar();
 50     }
 51     while(ch >= '0' && ch <= '9')
 52     {
 53         Ret = Ret * 10 + ch - '0';
 54         ch = getchar();
 55     }
 56     return Ret;
 57 }
 58 
 59 const int N = 40010;
 60 int n;
 61 int Prime[N], Tot;
 62 bool Visit[N];
 63 
 64 inline void GetPrime()
 65 {
 66     For(i, 2, N-1)
 67     {
 68         if(!Visit[i]) Prime[++Tot] = i;
 69         For(j, 1, Tot)
 70         {
 71             if(i * Prime[j] >= N) break;
 72             Visit[i * Prime[j]] = 1;
 73             if(!(i % Prime[j])) break;
 74         }
 75     }
 76 }
 77 
 78 inline void Solve();
 79 
 80 inline void Input()
 81 {
 82     GetPrime();
 83     int TestNumber = Getint();
 84     while(TestNumber--)
 85     {
 86         n = Getint();
 87         Solve();
 88     }
 89 }
 90 
 91 inline void Solve()
 92 {
 93     if(n == 1)
 94     {
 95         puts("0");
 96         return;
 97     }
 98     
 99     LL Total = 1, Except = n;
100     For(i, 1, Tot)
101     {
102         if(Prime[i] * Prime[i] > n) break;
103         if(!(n % Prime[i]))
104         {
105             int Fact = 1;
106             LL Cnt = 1;
107             while(!(n % Prime[i]))
108             {
109                 Cnt *= Prime[i];
110                 Fact++;
111                 n /= Prime[i];
112             }
113             Except *= Fact;
114             Cnt *= Prime[i];
115             LL a = (Cnt - 1) / (Prime[i] - 1), b = Cnt + 1, c = Prime[i] + 1;
116             Total *= ((a / c) * (b / c) * c + a % c * (b / c) + b % c * (a / c));
117             //cout << Total << ' ' << Except << endl;
118         }
119     }
120     
121     if(n > 1) Except <<= 1, Total *= (1 + 1LL * n * n);
122     cout << Total - Except << endl;
123 }
124 
125 int main()
126 {
127     SetIO("1002");
128     Input();
129     //Solve();
130     return 0;
131 }
View Code

 

posted @ 2015-11-04 20:11  yanzx6  阅读(1044)  评论(0)    收藏  举报