差分约束系统详解
差分约束系统
差分约束系统即给一些限制条件,问你满足条件的最优解(最大最小值),或者判断添加你是否成立。
解的存在性
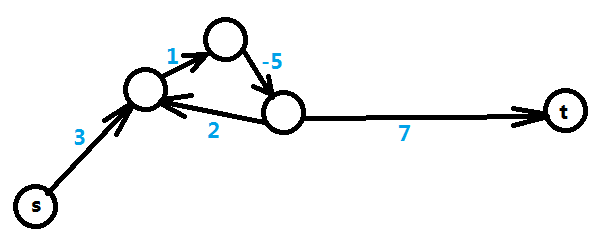
差分约束系统中,有两种特殊情况,1种是出现负权圈时, 如下图,求\(arr[t] - arr[s]\)的最大值, 这时 s 到 t 不存在最短路, 即最大值不纯在。
还有一种情况是 s 和 t 没有约束关系,如下图所示。这时他们得最大值为正无穷最小值为负无穷。
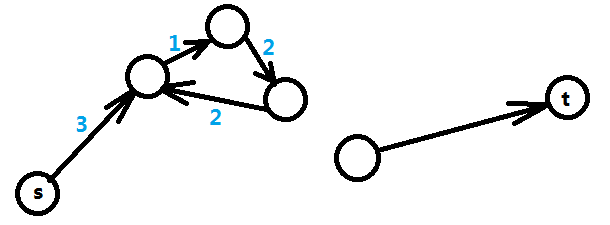
即解的情况有三种:有解, 无解, 无限多解。
不等式标准化
在求解差分约束系统的最优解时, 我们需要将不等式标准化。这时我们要根据题目中的要求做相应变换。如果题目要求最大值,我们则将不等式化作\(a[i] - a[j] <= t\),建一条 j --> i 的权值为t边, 并求最短路;反之要求最小值,我们则将不等式化作\(a[i] - a[j] >= t\), 建一条 j --> i 的权值为t的边, 并求最长路。
还有需要建的几种特殊的边。如果题目约束 \(a[i] - a[j] == t\),那么我们可以将式子转化成下面两个式子:
再将其中一种不等号反向, 建图即可。
同时如果题目要求\(a[i] - a[j] < t\), 那么在整数条件下我们可以将其改为\(a[i] - a[j] <= t - 1\),实数的话加个eps即可。
ps:在判断有无负环时, 我们用dfs比较好, 因为用bfs可能会mle或tle。
例题
模板题
【描述】:n 个未知数, m 个不等式形如\(a - b >= c\), 有解则输出一组解, 无解则输出NO。
【思路】:直接差分约束, 用一下超级源点的思想从0给所有未知数加个权值为0的边, 最后泡一下spfa(0),有解则dis[i]就是满足要求的每个未知数的解。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 4e5 + 10;
const int inf = 0x3f3f3f3f;
int gcd(int a,int b) { return b == 0 ? a : gcd(b, a % b); }
struct farm{
int nex, to, val;
}Edge[maxn<<1];
int head[maxn], n, m, tot;
queue<int> q;
int vis[maxn], dis[maxn], mk[maxn];
inline void init(){
tot = 0;
memset(head, -1, sizeof(head));
}
inline void add(int from, int to, int val){
Edge[++tot].to = to;
Edge[tot].val = val;
Edge[tot].nex = head[from];
head[from] = tot;
}
bool spfa(int s)
{
for(int i = 1; i <= n; ++i){
mk[i] = vis[i] = 0;
dis[i] = i == s ? 0 : inf;
}
q.push(s);
vis[s] = 1; mk[s]++;
while(!q.empty()){
int u = q.front();
q.pop();
vis[u] = 0;
for(int i = head[u]; i != -1; i = Edge[i].nex){
int v = Edge[i].to;
if(dis[v] > dis[u] + Edge[i].val){
dis[v] = dis[u] + Edge[i].val;
if(vis[v]) continue;
vis[v] = 1;
if(++mk[v] >= n) return 0;
q.push(v);
}
}
}
return 1;
}
int main()
{
scanf("%d %d", &n, &m);
init();
for(int i = 1; i <= m; ++i){
int a, b, val;
scanf("%d %d %d", &a, &b, &val);
add(b, a, val);
}
for(int i = 0; i <= n; ++i){
add(0, i, 0);
}
int ok = spfa(0);
if(!ok) puts("NO");
else{
for(int i = 1; i <= n; ++i){
printf("%d%c", dis[i], i == n ? '\n' : ' ');
}
}
system("pause");
}
P1250种树
【描述】:n 个区域编号 1...n,m 个房子,每个房子都有一个要求:在s ~ t 区域内至少种 val 棵树, 问最少种即可树满足要求?
【思路】:这题求得是最小值, 我们可以将不等式化成 ">=" 的形式, 用前缀和来表示, a - b中至少有val棵树, 即:\(sum[a] - sum[b-1] >= val\), 故可建 (b-1) --> a 的权值为 val 的边, 同时还有一个约束条件:\(1 >= sum[i] - sum[i-1] >= 0\),即:\(sum[i] - sum[i-1] >= 0\), \(sum[i-1] - sum[i] >= -1\);即建(i - 1) --> i的权值为0的边和i --> (i-1)的权值为-1的边, 最后spfa跑一边最长路, 输出dis[n]即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 2e5 + 10;
const int inf = 0x3f3f3f3f;
int gcd(int a,int b) { return b == 0 ? a : gcd(b, a % b); }
int n, m;
int dis[maxn], vis[maxn], tot;
struct edge{
int nex, to, val;
}Edge[maxn];
int head[maxn];
inline void add(int from, int to, int val){
Edge[++tot].to = to;
Edge[tot].val = val;
Edge[tot].nex = head[from];
head[from] = tot;
}
void spfa(int s)
{
for(int i = 0; i <= n; ++i){
dis[i] = -inf;
vis[i] = 0;
}
queue<int> q;
q.push(s);
dis[s] = 0; vis[s] = 1;
while(!q.empty())
{
int u = q.front();
q.pop();
vis[u] = 0;
for(int i = head[u]; i != -1; i = Edge[i].nex){
int v = Edge[i].to;
if(dis[v] < dis[u] + Edge[i].val){
dis[v] = dis[u] + Edge[i].val;
if(vis[v]) continue;
vis[v] = 1;
q.push(v);
}
}
}
}
int main()
{
scanf("%d %d", &n, &m);
memset(head, -1, sizeof(head));
for(int i = 1; i <= m; ++i){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add(a-1, b, c);
}
for(int i = 1; i <= n; ++i){
add(i - 1, i, 0);
add(i, i - 1, -1);
}
spfa(0);
printf("%d\n", dis[n]);
system("pause");
}
P1993 小K的农场
【描述】:n 个农场, m个不等式, 1开头表示 a 比 b 至少多 val 个, 2开头表示a 比 b 至多多多少个, 3开头表示 a 和 b 相等, 问有没有解。n, m 都是 1e4 范围。
【思路】:差分约束判断负环即可。spfa判断负环时间复杂度为\(O(nm)\), 在这可能会超时, 所以用dfs模拟一下即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 2e5 + 10;
const int inf = 0x3f3f3f3f;
int gcd(int a,int b) { return b == 0 ? a : gcd(b, a % b); }
struct edge{
int nex, to, val;
}Edge[maxn];
int head[maxn], tot, n, m;
int dis[maxn], mk[maxn], vis[maxn];
inline void add(int from, int to, int val){
Edge[++tot].to = to;
Edge[tot].val = val;
Edge[tot].nex = head[from];
head[from] = tot;
}
bool spfa(int u){
vis[u] = 1;
for(int i = head[u]; i != -1; i = Edge[i].nex){
int v = Edge[i].to;
if(dis[v] < dis[u] + Edge[i].val){
dis[v] = dis[u] + Edge[i].val;
if(vis[v]) return 0;
if(!spfa(v)) return 0;
}
}
vis[u] = 0;
return 1;
}
int main()
{
scanf("%d %d", &n, &m);
memset(head, -1, sizeof(head));
for(int i = 1; i <= m; ++i){
int a, b, val, f;
scanf("%d %d %d", &f, &a, &b);
if(f == 1){
scanf("%d", &val);
add(b, a, val);
}
else if(f == 2){
scanf("%d", &val);
add(a, b, -val);
}
else{
add(b, a, 0);
add(a, b, 0);
}
}
for(int i = 1; i <= n; ++i){
add(0, i, 0);
dis[i] = -inf;
}
if(spfa(0)) puts("Yes");
else puts("No");
system("pause");
}


