高斯消元解线性期望方程的妙用
BZOJ3143
http://www.lydsy.com/JudgeOnline/problem.php?id=3143
Ei表示经i点的期望
E(u,v)表示经(u,v)的期望
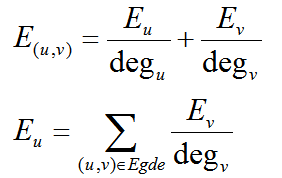
特别地有
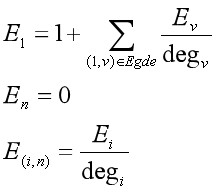
构造线性期望方程,高斯消元即可.
根据排序不等式,贪心即可
#include<cstdio>
#include<algorithm>
using namespace std;
double a[511][511],x[511],w[250011],ans;
int deg[511];
int u[250011],v[250011];
int n,m;
inline void init(){
for(register int i=1;i<=m;++i){
a[u[i]][v[i]]+=1.00/deg[v[i]];
a[v[i]][u[i]]+=1.00/deg[u[i]];
}
for(register int i=1;i<n;++i)
a[i][i]=-1.00;
a[1][n+1]=-1.00;
for(register int i=1;i<=n+1;++i)
a[n][i]=0.00;
a[n][n]=1.00;
}
inline void gauss(){
double tmp;
for(register int i=1,p;i<=n;++i)
for(register int j=i+1;j<=n;++j){
tmp=1.00*a[j][i]/a[i][i];
for(register int k=i;k<=n+1;++k)
a[j][k]-=1.00*a[i][k]*tmp;
}
for(register int i=n;i;--i){
for(register int j=i+1;j<=n;++j)a[i][n+1]-=x[j]*a[i][j];
x[i]=a[i][n+1]/a[i][i];
}
}
inline bool cmp(double a,double b){
return a>b;
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;++i){
scanf("%d%d",v+i,u+i);
++deg[v[i]];++deg[u[i]];
}
init();
gauss();
for(register int i=1;i<=m;++i)w[i]=1.00*x[u[i]]/(1.00*deg[u[i]])+1.00*x[v[i]]/(1.00*deg[v[i]]);
sort(w+1,w+m+1,cmp);
for(register int i=1;i<=m;++i)
ans+=1.00*i*w[i];
printf("%.3lf",ans);
return 0;
}
BZOJ2337
http://www.lydsy.com/JudgeOnline/problem.php?id=2337
按二进制枚举每位,然后做法类似与上面
Ei表示i到n的二进制第k位为1的期望

对于每次消元后对E1*2k求个和
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1e6+7;
double a[501][501],_x[501],ans;
int nxt[maxn],las[maxn],to[maxn],w[maxn],deg[maxn];
int n,m,x,y,z,tot;
inline void add(int x,int y,int z){
nxt[++tot]=las[x];
las[x]=tot;
to[tot]=y;
w[tot]=z;
++deg[y];
}
inline void gauss(){
double tmp;
for(register int i=1,p;i<=n;++i){
p=i;
while(!a[p][i])++p;
if(p!=i)swap(a[p],a[i]);
for(register int j=i+1;j<=n;++j){
tmp=a[j][i]/a[i][i];
for(register int k=i;k<=n+1;++k)
a[j][k]-=1.00*a[i][k]*tmp;
}
}
for(register int i=n;i;--i){
for(register int j=i+1;j<=n;++j)
a[i][n+1]-=1.00*_x[j]*a[i][j];
_x[i]=a[i][n+1]/a[i][i];
}
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;++i){
scanf("%d%d%d",&x,&y,&z);
if(x!=y)add(x,y,z),add(y,x,z);
else add(x,y,z);
}
for(register int i=0;i<=30;++i){
for(register int i=1;i<=n;++i)
for(register int j=1;j<=n+1;++j)
a[i][j]=0.00;
for(register int j=1;j<n;++j){
a[j][j]=1.00;
for(register int e=las[j];e;e=nxt[e]){
x=to[e];
if((w[e]>>i)&1){
a[j][x]+=1.00/deg[j];
a[j][n+1]+=1.00/deg[j];
}
else
a[j][x]-=1.00/deg[j];
}
}
a[n][n]=1.00;
gauss();
ans+=1.00*_x[1]*(1<<i);
}
printf("%.3lf\n",ans);
return 0;
}
BZOJ3534
http://www.lydsy.com/JudgeOnline/problem.php?id=3534
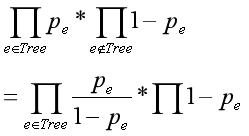
就是求这一坨,新边权为![]()
结合矩阵树定理,构造行列式,做高斯消元,最后乘上后面那一坨就好了
#include<cstdio>
#include<algorithm>
using namespace std;
const int mod=998244353;
typedef double db;
db a[5001][5001],ans;
int x,y,n,m;
inline db fabs(db x){
return x>=0?x:-x;
}
inline db gauss(){
db tmp;
for(register int i=1,t;i<n;++i){
t=i;
for(register int j=i+1;j<n;++j)
if(fabs(a[t][i])<fabs(a[j][i]))
t=j;
if(!a[t][i])return 0.00;
swap(a[t],a[i]);
for(register int j=i+1;j<n;++j){
tmp=1.00*a[j][i]/a[i][i];
for(register int k=i;k<n;++k)
a[j][k]-=1.00*a[i][k]*tmp;
}
}
tmp=1.00;
for(register int i=1;i<n;++i)
tmp=tmp*a[i][i];
return fabs(tmp);
}
int main(){
scanf("%d",&n);
ans=1;
for(register int i=1;i<=n;++i)
for(register int j=1;j<=n;++j){
scanf("%lf",&a[i][j]);
if(i==j)continue;
if(i<j)ans=ans*(1.00-a[i][j]);
a[i][j]=a[i][j]/(1.00-a[i][j]);
}
for(register int i=1;i<=n;++i)
for(register int j=1;j<=n;++j)
if(i!=j)
a[i][i]-=a[i][j];
ans=ans*gauss();
printf("%.8lf",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号