BZOJ4176&&BZOJ3994

BZOJ 4176 http://www.lydsy.com/JudgeOnline/problem.php?id=4176

 莫比乌斯反演+杜教筛

 

 

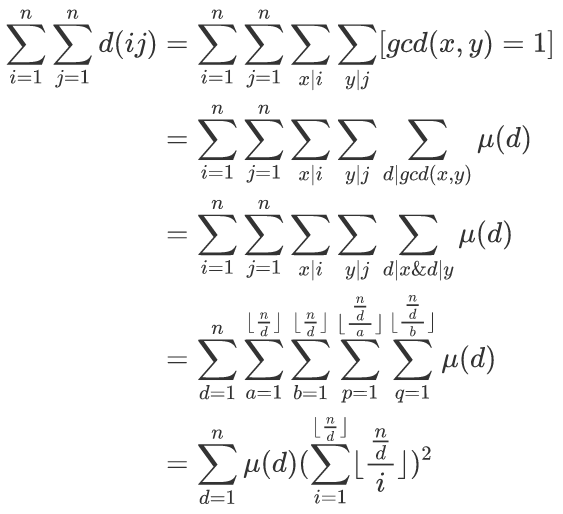
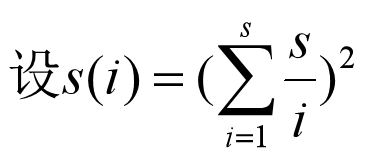
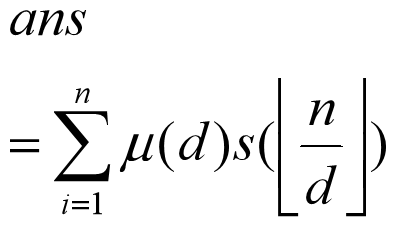
好像μ可以杜教筛肛

　　s可以有√n的做法

复杂度为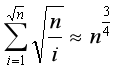

 

 

#include<cstdio>
#include<cmath>
#include<map>
typedef long long ll;
std::map<ll,int>m1;
std::map<ll,ll>m2;
std::map<ll,bool>vis1,vis2;
const int N=10000011;
const int mod=1000000007;
bool ip[N];
int pr[N],miu[N];
int pos,blo;
ll ans,n;
inline void shai_fa(){
	miu[1]=1;
	for(register int i=2;i<=blo;++i){
		if(!ip[i])
			miu[pr[++pr[0]]=i]=-1;
		for(register int j=1;j<=pr[0]&&pr[j]*i<=blo;++j){
			ip[i*pr[j]]=1;
			if(i%pr[j]==0)
				break;
			miu[i*pr[j]]=-miu[i];
		}
	}
	for(register int i=1;i<=blo;++i)
		miu[i]=miu[i-1]+miu[i];
}
inline int getmiu(ll x){
	if(x<=blo)return miu[x];
	if(vis1[x])return m1[x];
	int ans=1;
	ll pos;
	for(register ll i=2;i<=x;i=pos+1){
		pos=x/(x/i);
		ans-=(pos-i+1)*getmiu(x/i);
		if(ans<0)
			ans+=mod;
	}
	vis1[x]=1;
	return m1[x]=ans;
}
inline ll getf(ll x){
	if(vis2[x])return m2[x];
	ll ans=0,pos;
	for(register ll i=1;i<=x;i=pos+1){
		pos=x/(x/i);
		ans+=1ll*(pos-i+1)%mod*(x/i);
		ans%=mod;
	}
	vis2[x]=1;
	return m2[x]=1ll*ans*ans%mod;
}
int main(){
	scanf("%lld",&n);
	blo=pow(n,2.00/3.00);
	shai_fa();
	for(register ll i=1,pos;i<=n;i=pos+1){
		pos=n/(n/i);
		ans+=1ll*(getmiu(pos)-getmiu(i-1))*getf(n/i)%mod;
		ans=(ans+mod)%mod; 
	}
	printf("%lld\n",ans);
	return 0;
} 

　　

BZOJ3994 http://www.lydsy.com/JudgeOnline/problem.php?id=3994

这只是多了一个打表预处理S(i)的过程

#include<cstdio>
#define FOR(i,s,t) for(register int i=s;i<=t;++i)
inline int min(int a,int b){return a<b?a:b;}
typedef long long ll;
const int N=50011,maxn=50000;
int miu[N],pr[N/12];
ll ans[N];
ll res;
bool ip[N];
int pos;
inline void shai_fa(){
    miu[1]=1;
    for(register int i=2;i<=maxn;++i){
        if(!ip[i])
            miu[pr[++pr[0]]=i]=-1;
        for(register int j=1;j<=pr[0]&&pr[j]*i<=maxn;++j){
            ip[i*pr[j]]=1;
            if(i%pr[j]==0)break;
            miu[i*pr[j]]=-miu[i];	
        }	
    }
    for(register int i=1;i<=maxn;++i)
        miu[i]+=miu[i-1];
}
inline ll getf(int x){
    int pos;
    ll ans=0;
    for(register int i=1;i<=x;i=pos+1){
        pos=x/(x/i);
        ans+=1ll*(pos-i+1)*(x/i);
    }
    return ans;
}
int n,m,T;
int main(){
    shai_fa();
    FOR(i,1,maxn)ans[i]=getf(i);
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        res=0;
        for(register int i=1;i<=min(n,m);i=pos+1){
            pos=min(n/(n/i),m/(m/i));
            res+=1ll*(miu[pos]-miu[i-1])*ans[n/i]*ans[m/i];
        }
        printf("%lld\n",res);
    }
    return 0;
}