luogu P1270 “访问”美术馆

题目描述

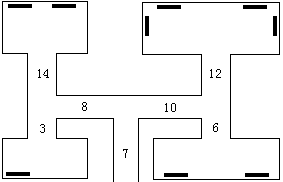
经过数月的精心准备，Peer Brelstet，一个出了名的盗画者，准备开始他的下一个行动。艺术馆的结构，每条走廊要么分叉为两条走廊，要么通向一个展览室。Peer知道每个展室里藏画的数量，并且他精确测量了通过每条走廊的时间。由于经验老到，他拿下一幅画需要5秒的时间。你的任务是编一个程序，计算在警察赶来之前，他最多能偷到多少幅画。

输入输出格式

输入格式：

 

第1行是警察赶到的时间，以s为单位。第2行描述了艺术馆的结构，是一串非负整数，成对地出现：每一对的第一个数是走过一条走廊的时间，第2个数是它末端的藏画数量；如果第2个数是0，那么说明这条走廊分叉为两条另外的走廊。数据按照深度优先的次序给出，请看样例。

一个展室最多有20幅画。通过每个走廊的时间不超过20s。艺术馆最多有100个展室。警察赶到的时间在10min以内。

 

输出格式：

 

输出偷到的画的数量

 

输入输出样例

输入样例#1：

60
7 0 8 0 3 1 14 2 10 0 12 4 6 2

输出样例#1：

2

题目链接：https://www.luogu.org/problem/show?pid=1270

解题报告

很明显，这是一道树形背包DP.

首先,输入就要模拟二叉树的dfs序.

所以,美术馆的门口为根进行dfs,复杂度为O(n).

定义f[now][j]表示到达第now号点花j的时间可以获得的最大价值.

对于走廊的尽头，即叶子结点,

状态转移方程为f[now][i]=min((i-p[now].len)/5,p[now].num).

对于走廊来说，

状态转移方程为

对于左儿子:left_son:f[now][i]=max(f[now][i],f[now][i-j]+f[p[now].l][j]),

对于右儿子:right_son:f[now][i]=max(f[now][i],f[now][i-j]+f[p[now].r][j]).

对于状态转移的复杂度为O(m²).

所以,总复杂度为O(n*m²).

AC代码如下:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#define FOR(i,s,t) for(register int i=s;i<=t;++i)
using namespace std;
int f[5001][601];
int nxt[1011],to[1011],las[1011];
int m,tot;
struct node{
    int l;
    int r;
    int len;
    int num;
}p[5011];
int read(){
    char c=getchar();
    while((c<'0'||c>'9')&&c!='-')
        c=getchar();
    int data=0,w=1;
    if(c=='-')
        w=-1,c=getchar();
    while(c>='0'&&c<='9')
        data=(data<<1)+(data<<3)+c-'0',c=getchar();
    return data;
}
void build(int now){
    p[now].len=read();
    p[now].len=p[now].len<<1;
    p[now].num=read();
    if(p[now].num)
        return ;
    build(p[now].l=++tot);
    build(p[now].r=++tot);    
}
void dfs(int now){
    if(p[now].num){
        for(register int i=m;i>p[now].len;--i)
            f[now][i]=min((i-p[now].len)/5,p[now].num);
        return ;
    }
    dfs(p[now].l);
    for(register int i=m;i>=p[now].len;--i)
        for(register int j=1;j<=i-p[now].len;++j)
            f[now][i]=max(f[now][i],f[now][i-j]+f[p[now].l][j]);
    dfs(p[now].r);
    for(register int i=m;i>=p[now].len;--i)
        for(register int j=1;j<=i-p[now].len;++j)
            f[now][i]=max(f[now][i],f[now][i-j]+f[p[now].r][j]);
}
int main(){
    m=read();
    --m;
    build(++tot);
    dfs(1);
    printf("%d\n",f[1][m]);
    return 0;
}