算法--旅行者过河问题
1.题目
在漆黑的夜里,四位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话,大家是无论如何也不敢过桥去的。不幸的是,四个人一共只带了一只手电筒,而桥窄得只够让两个人同时过。如果各自单独过桥的话,四人所需要的时间分别是1、2、5、8分钟;而如果两人同时过桥,所需要的时间就是走得比较慢的那个人单独行动时所需的时间。问题是,如何设计一个方案,让这四人尽快过桥。
2.算法
构造N个人(N≥1)过桥最佳方案的方法:
设A、B为走得最快和次快的旅行者,过桥所需时间分别为a、b;而Z、Y为走得最慢和次慢的旅行者,过桥所需时间分别为z、y。
1) 如果N=2,AB一起过桥。
t=b
2) 如果N=3,ABC三人,A+C过,A回;A+B过。t=a+b+c
3) 如果N≥4,那么有两种过河模式,将ZY送到对岸,人数-2:模式一:A+Z过,A回;A+Y过,A回
t1=2*a+y+z
模式二:A+B过,A回;Z+Y过,B回
t2=a+2*b+z
比较两种模式:
t1-t2=a+y-2b
当2b>a+y时,t1<t2,使用模式一;
否则,使用模式二。
这样下来每次人数-2,直到人数<4时结束递归,得到过河消耗的时间。
3.代码
import java.util.Arrays; import java.util.Scanner; /** * @author Administrator */ public class River { public static void main(String[] args){ Scanner sc=new Scanner(System.in); System.out.println("请输入过河人数:"); int n=sc.nextInt(); int[] a=new int[n]; System.out.println("请输入过河人员情况:"); for(int i=0;i<n;i++){ a[i]=sc.nextInt(); } Arrays.sort(a); System.out.println(getMinTime(a,n)); } /** * 递归,n人过河时间=(n-2)人过河时间+送走时间最长的两个人消耗时间 * @param a 过河人员情况 * @param n 每次递归的人即为a的前n位(n每次递归-2,当n<4时,递归结束) * @return 返回每个阶段的时间,直到结束 */ public static int getMinTime(int[] a,int n){ if(n==3){ return a[0]+a[1]+a[2]; } else if(n==2){ return a[1]; } //判断两个模式应该选择哪一种 int t1=2*a[0]+a[n-2]+a[n-1]; int t2=a[0]+2*a[1]+a[n-1]; int t; if((a[0]+a[n-2])<(2*a[1])){ t=t1; } else{ t=t2; } return getMinTime(a,n-2)+t; } }
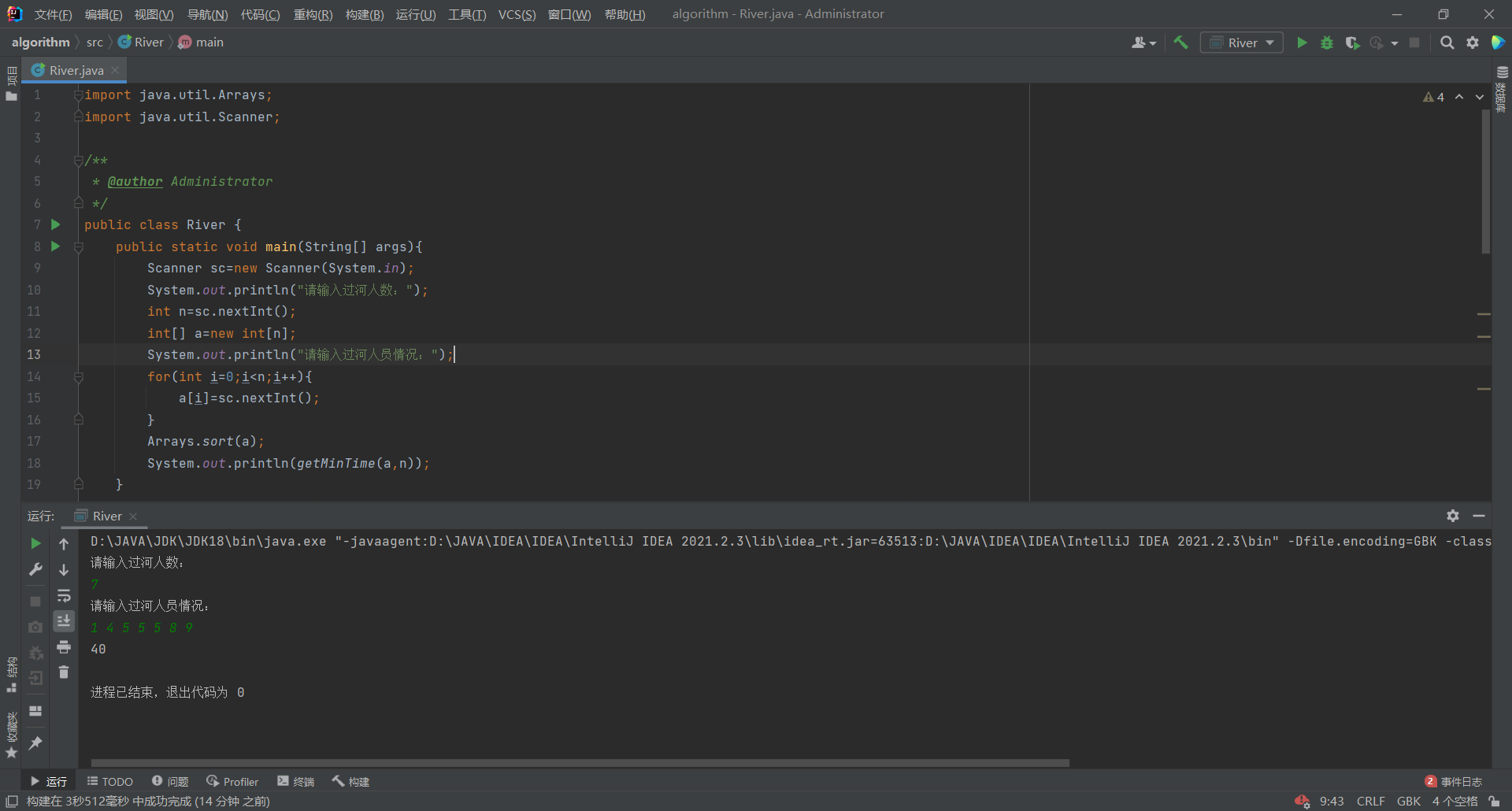
4.结果



 浙公网安备 33010602011771号
浙公网安备 33010602011771号