AcWing. 323. 战略游戏

题意简述

$$ 给定一棵树，要求树中任意一边至少选中一点，求最少满足题意的选点数

解题思路

$$我们可以先画出示意图来

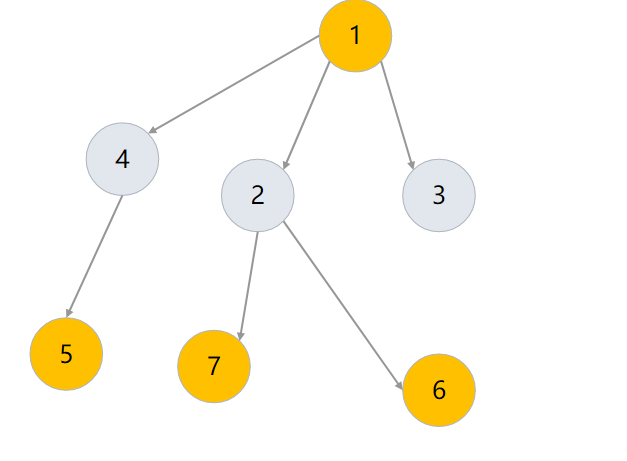
橙色点表示选，灰色点表示不选。
$$我们可以用 $f[i][j],j\in [0,1]$ 来表示目前在考虑第i个点，选择情况是j，当 $j=0$代表不选第 $i$ 个点，当 $j=1$ 代表要选。
$$容易得出状态转移方程：对于父节点 $fa$ ，子节点 $son$， 当父节点不选的时候，由于一条边至少选一点，子节点必须选，所以 $f[fa][0]$ 只能从 $f[son][1]$ 转移，而父节点要选的时候，不论选不选子节点都可以符合题目要求，所以有两种转移方式

代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1550;
int h[N], e[N], ne[N], idx;
int f[N][2], is_son[N], n;

void add(int a, int b) 
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u) 
{
    f[u][0] = 0, f[u][1] = 1;
    for (int i = h[u]; ~i; i = ne[i]) 
    {
        int j = e[i];
        dfs(j);
        f[u][0] += f[j][1];
        f[u][1] += min(f[j][0], f[j][1]);
    }
}

int main() 
{
    while (~scanf("%d", &n)) 
    {
        memset(is_son, 0, sizeof is_son);
        memset(h, -1, sizeof h), idx = 0;

        while (n -- )
        {
            int u, son, sum;
            scanf("%d:(%d) ", &u, &sum);
            while (sum -- ) 
            {
                scanf("%d", &son);
                add(u, son);
                is_son[son] = true;
            }
        }

        int root = 0;
        while (is_son[root]) root ++ ;
        dfs(root);
        printf("%d\n", min(f[root][1], f[root][0]));
    }

    return 0;
}