YBTOJ 6.3同余问题
A.同余方程
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
void exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1;
y = 0;
return;
}
exgcd(b, a % b, x, y);
ll z = x;
x = y;
y = z - (a / b) * y;
}
int main() {
ll a, b, x, y;
scanf("%lld%lld", &a, &b);
exgcd(a, b, x, y);
x = (x + b) % b;
printf("%lld",x);
return 0;
}
B.约数之和
考虑算术基本定理
求
\(\prod\limits_{i = 1}^n\sum\limits_{j = 0}^{b \times c_i} p_i^j\)
根据等比数列求和公式 得
\(\prod\limits_{i = 1}^n (\frac{p_i^{b \times c_i + 1} - 1}{p_i - 1})\)
考虑 \(p_i - 1\) 与 \(9901\) 不互质的情况
则有 \(p_i - 1 \equiv 0 (\text{mod } 9901)\)
\(p_i \equiv 1 (\text{mod } 9901)\)
那么对于任意 \(x\) 都有 \(p_i^x \equiv 1 (\text{mod } 9901)\)
那么显然 \(\sum\limits_{j = 0}^{b \times c_i} p_i^j \mod 9901= b \times c_i + 1\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 9901;
ll a, b, ans = 1;
int tot;
ll ksm(ll x, ll y) {
ll ret = 1;
while (y) {
if (y & 1) ret = ret * x % mod;
x = x * x % mod;
y >>= 1;
}
return ret;
}
ll inv(ll x) {
return ksm(x, mod - 2);
}
void work(ll x, ll y) {
if ((x - 1) % mod == 0) ans = (ans * (b + 1) % mod) % mod;
else ans = (ans * (ksm(x, y + 1) - 1) % mod * inv(x - 1)) % mod;
}
int main() {
scanf("%lld%lld", &a, &b);
for (ll i = 2; i * i <= a; ++i) {
if (a % i == 0) {
int num = 0;
while (a % i == 0) {
a /= i;
num++;
}
work(i, num * b);
}
}
if (a > 1) work(a, 1 * b);
printf("%lld",ans);
return 0;
}
C.线性求逆元
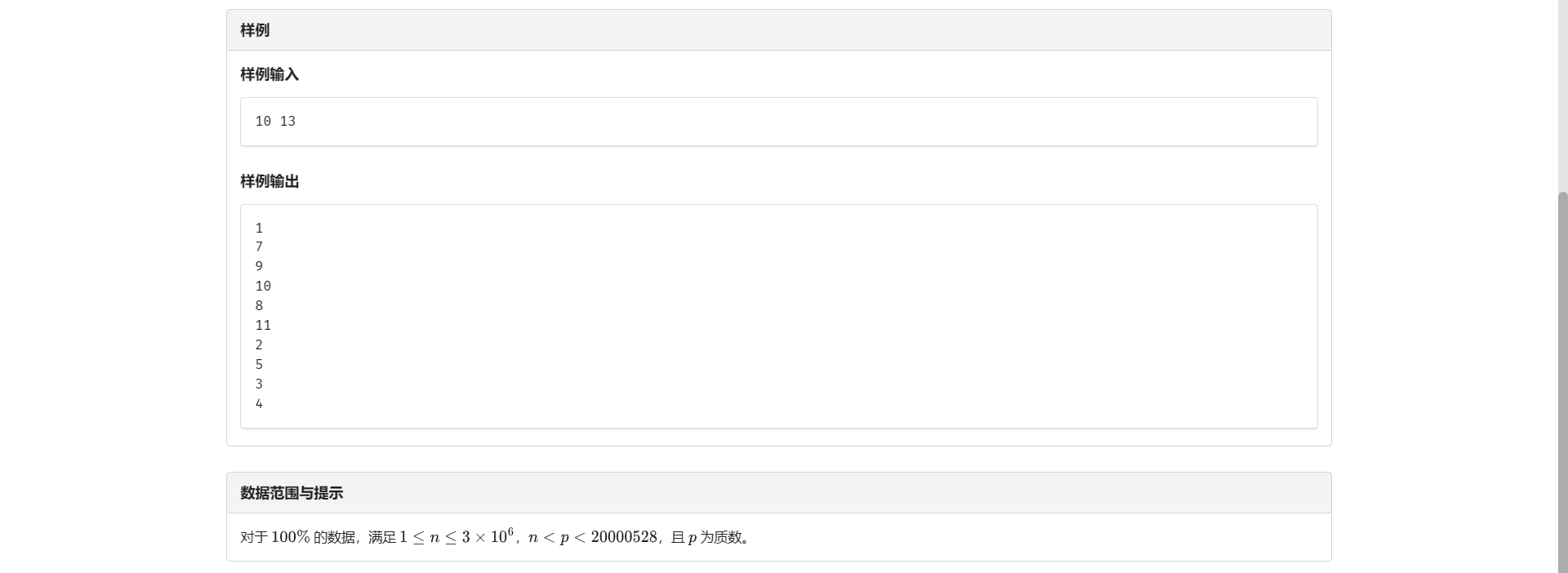
- 解法1
考虑构造 \(mod = \left\lfloor\dfrac{mod}{x}\right\rfloor \times x + r\)
转化为 \(\left\lfloor\dfrac{mod}{x}\right\rfloor \times x + r \equiv 0 (\text{mod } mod)\)
同乘 \(x^{-1} \times r^{-1}\) 得
\(\left\lfloor\dfrac{mod}{x}\right\rfloor \times r^{-1} + x^{-1} \equiv 0 (\text{mod } mod)\)
所以有
\(x^{-1} \equiv -\left\lfloor\dfrac{mod}{x}\right\rfloor \times r^{-1} (\text{mod } mod)\)
由于 \(r = mod \mod x\)
显然 \(r < x\)
也就是说我们已经知道了 \(r^{-1}\) 就可以直接求出 \(x^{-1}\) 了
inv[1] = 1;
for (int i = 2; i <= n; ++i) {
inv[i] = ((p - p / i) * inv[p % i] + p) % p;
}
- 解法二
来自 @rabbit_lb 可用来求阶乘的逆元
首先用快速幂求出 \(n!^{-1}\)
那么 \((n - 1)!^{-1} = n!^{-1} \times n\)
然后一直推下去即可
D.中国剩余定理
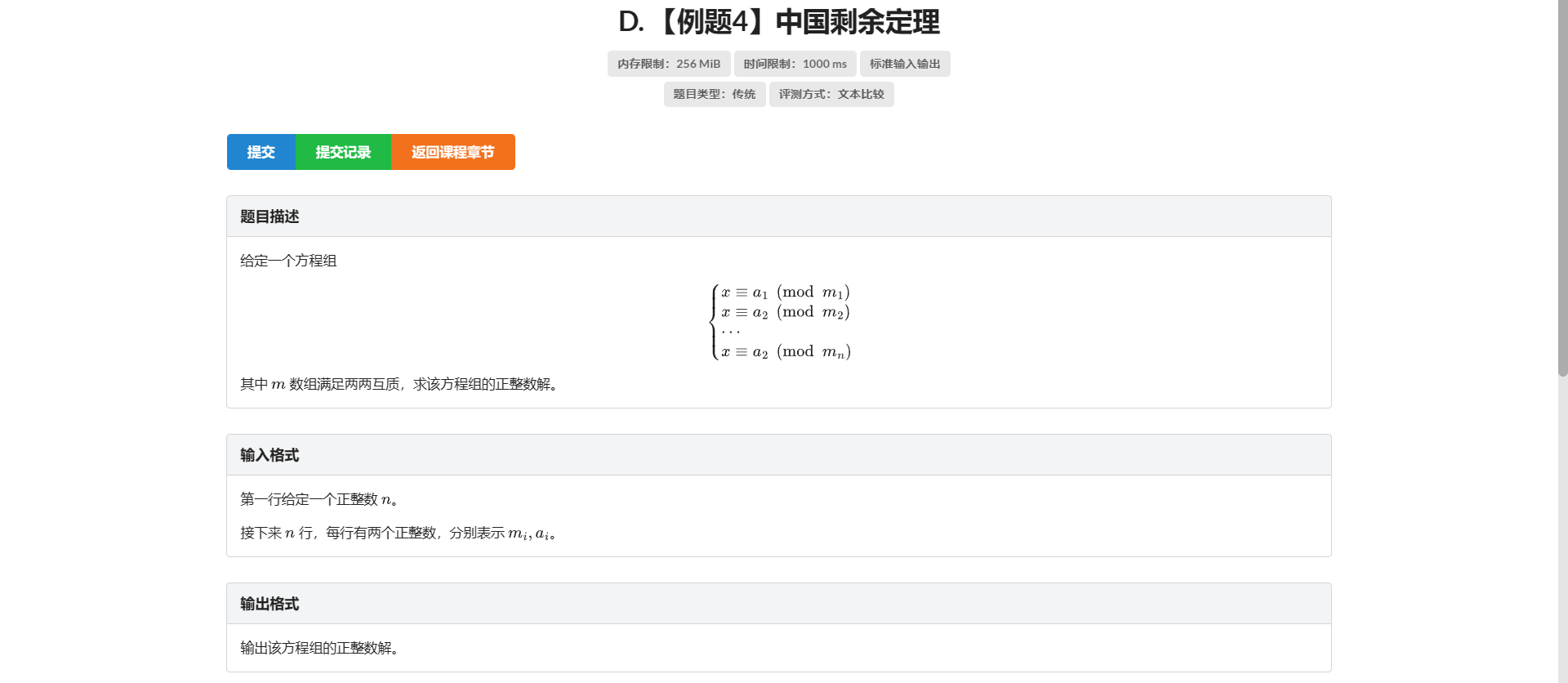
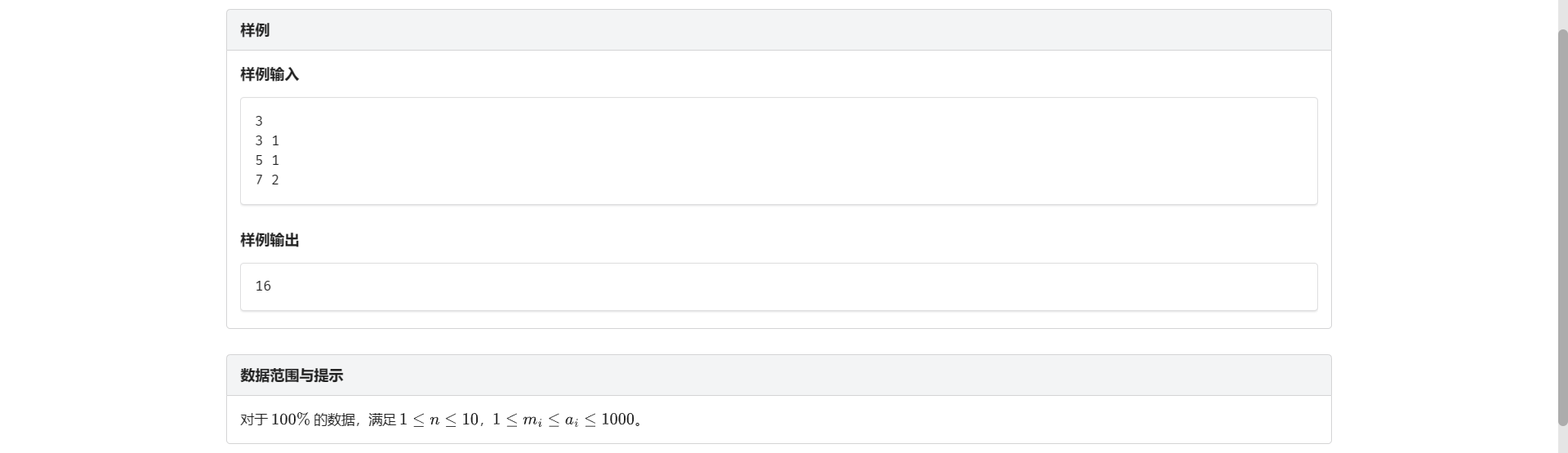
这章怎么全是板子题
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 11;
ll a[N], b[N];
ll pai = 1;
int k;
ll ans;
ll ksc(ll x, ll y) {
ll ret = 0;
while (y) {
if (y & 1) ret = (ret + x) % pai;
x = (x + x) % pai;
y >>= 1;
}
return ret;
}
void exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1;
y = 0;
return;
}
exgcd(b, a % b, x, y);
ll z = x;
x = y;
y = z - (a / b) * y;
}
int main() {
scanf("%d", &k);
for (int i = 1; i <= k; ++i) scanf("%lld%lld", &b[i], &a[i]);
for (int i = 1; i <= k; ++i) pai *= b[i];
for (int i = 1; i <= k; ++i) {
ll x, y;
exgcd(pai / b[i], b[i], x, y);
x = (x % b[i] + b[i]) % b[i];
a[i] = (a[i] % b[i] + b[i]) % b[i];
ans = (ans + ksc(pai / b[i] * x, a[i])) % pai;
}
printf("%lld", ans);
return 0;
}
