LCT学习笔记
可能不太算前置的前置:树链剖分学习笔记
非常算前置的前置:平衡树之Splay
基本概念
\(LCT\) 全名 \(Link-Cut-Tree\) 是一种支持在树上删边/加边然后维护两点间路径上信息的一个东西
首先我们要把这棵树进行虚实链剖分
然后对于每一条链都用一棵 \(Splay\) 来维护 并且以它的深度作为它在 \(Splay\) 中的权值 对于虚边 我们把它连接的儿子所属 \(Splay\) 的根节点连到父亲上
我们用一下luogu题解中的图
首先假如你现在是这么剖:
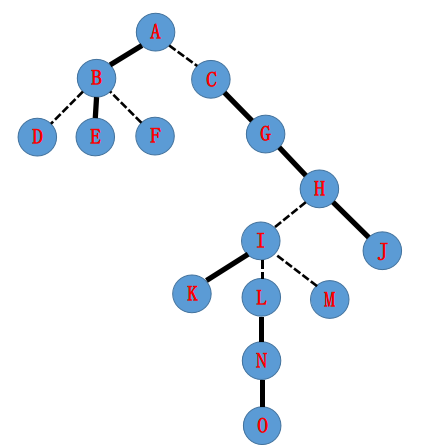
那么你的一车 \(Splay\) 大概就这么连:
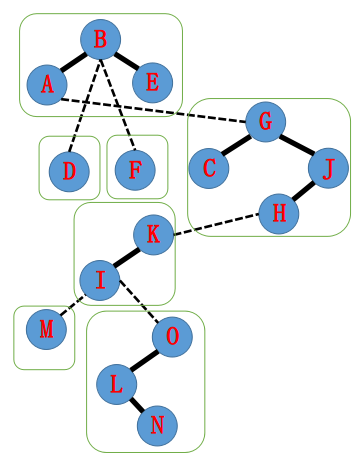
改装 \(Splay\)
所以我们首先要把 \(Splay\) 加以改装
以前因为只有一棵 我们直接判断它的父亲来看它是不是根节点即可
但是现在因为我们开了一车的 \(Splay\) 所以我们需要一个函数来判断它是不是自己所在的这棵 \(Splay\) 的根节点
显然如果它父亲的左右儿子都不是它 它就是自己这棵 \(Splay\) 的根节点了
inline bool isroot(int x) { //查询x是不是一棵splay的根
return son[fa[x]][0] != x && son[fa[x]][1] != x;
}
那么进一步的 我们的 \(rotate\) 和 \(splay\) 操作都需要改装一下:
void rotate(int x) {
int f = fa[x], gfa = fa[f];
bool i = get(x), i_ = get(f);
fa[x] = gfa;
if (!isroot(f)) son[gfa][i_] = x; //这地方变了 如果f是根就没有祖父 不要连 不然会连到别的splay上
son[f][i] = son[x][i ^ 1]; //而且一定要先写gfa那些东西 不然你底下改了f的父亲再判isroot就寄了
fa[son[x][i ^ 1]] = f;
son[x][i ^ 1] = f;
fa[f] = x;
update(x);
update(f);
}
void splay(int x) {
while (!isroot(x)) {
int f = fa[x];
if (!isroot(f)) {
if (get(f) == get(x)) rotate(f);
else rotate(x);
}
rotate(x);
}
update(x);
}
核心操作
然后我们讲一下 \(LCT\) 的一些核心操作
\(access\):把这个点到根节点的路径全变成实边
假如我 \(access(N)\) 大概就会变成这样:
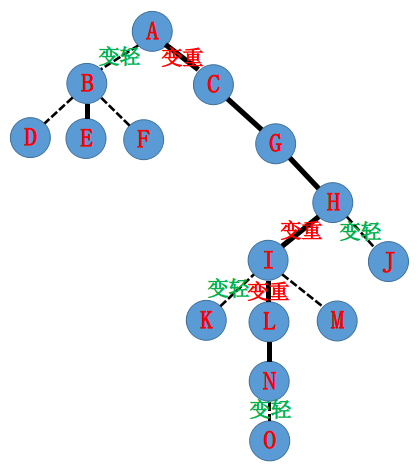
我们一步一步来
首先我们要把底下的断掉 在这里我们要把 \(N-O\) 断掉
由于 \(O\) 的深度更大 所以它在 \(Splay\) 中一定是 \(N\) 的右儿子
所以我们直接令 \(N\) 的右儿子为 \(0\) 即可
然后我们继续往上找断掉的边 所以我们先把当前的 \(N\) 旋到这棵 \(Splay\) 的顶端 发现需要连一条 \(I-N\):
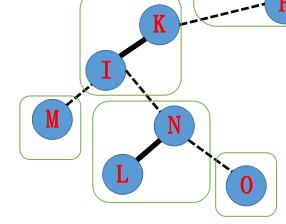
那么首先我们让 \(I\) 底下的断掉 还是把右儿子变成 \(0\)
然后我们要把 \(I\) 和 \(N\) 连上 所以我们把 \(I\) 的右儿子变成 \(N\)
然后我们再查 \(I\) 这条链的顶端 即把 \(I\) 旋上去
然后你就会发现如此循环往复做到根节点就行了
void access(int x) { //把x与根节点的边都连成实边
for (int y = 0; x; y = x, x = fa[x]) {
splay(x);
son[x][1] = y; //实际上是先让它等于0 然后连x 直接一步到位就行了
update(x);
}
}
\(makeroot\):让这个点成为整棵树的根节点
首先我们把这个点和根节点用 \(access\) 函数塞到一个 \(Splay\) 里面
然后把这个点旋到根节点
重点来了 因为我们 \(access\) 的时候事先断掉了这个点以下的部分 所以在这条链里 它的深度是最大的
换言之 也就是说现在所有的点在这棵 \(Splay\) 里都在它的左子树里
那么我们把这棵 \(Splay\) 所有的左右子树交换 现在所有点就都在它右子树里
这也意味着当前它是这条链上深度最小的点
那就是根节点了
当然暴力交换肯定不可取 我们参考文艺平衡树打 \(lazytag\)
inline void reverse(int x) { //左右儿子翻转
swap(son[x][0], son[x][1]);
lazy[x] ^= 1;
}
inline void pushdown(int x) {
if (lazy[x]) {
if (son[x][0]) reverse(son[x][0]);
if (son[x][1]) reverse(son[x][1]);
lazy[x] = 0;
}
}
void makeroot(int x) { //令x成为根节点
access(x);
splay(x); //此时x在splay的根节点
reverse(x); //access的时候x就是这条实链深度最深的点 所以在splay中x只有左儿子 把它们都翻转x就只有右儿子 此时就是这条链深度最浅的点 即为根节点
}
顺带一提 这样的话 \(Splay\) 操作也需要变一下:
void splay(int x) {
int tmp = x, top = 0;
st[++top] = x;
while (!isroot(tmp)) {
tmp = fa[tmp];
st[++top] = tmp;
}
for (int i = top; i; --i) pushdown(st[i]); //开一个栈把需要下传的节点都记录 然后从上往下下传
while (!isroot(x)) {
int f = fa[x];
if (!isroot(f)) {
if (get(f) == get(x)) rotate(f);
else rotate(x);
}
rotate(x);
}
update(x);
}
\(findroot\):查询当前点所在树的树根
首先还是得先把它和根节点塞到一棵 \(Splay\) 中
然后还是得把它旋到根节点
然后因为我们要查询根节点 即查深度最小的点 所以我们一直走左儿子走到不能走即可
记得下传 \(lazytag\)
int findroot(int x) { //查询x所在那条链的根节点
access(x);
splay(x);
while (son[x][0]) pushdown(x), x = son[x][0]; //一直往左走
splay(x); //保证复杂度
return x;
}
一些功能函数
最后是一些功能函数
\(split\):把两个点中间的路径上拉成一条链
首先我们把 \(x\) 拉到根
然后我们把 \(y\) 与根节点那条链拉起来
这条链就是我们要的那条
然后查询的时候把 \(y\) 旋到根结点 然后直接查询 \(y\) 对应的数组就是整棵 \(Splay\) 即整条链的信息(我感觉旋 \(x\) 查 \(x\) 是不是也行)
void split(int x, int y) { //把x到y的路径拉出来
makeroot(x); //让x成为根
access(y); //把x到y拉出来
splay(y);
}
···
LCT.split(x, y);
printf("%d\n", LCT.tr[y]); //因为有个splay 此时y是splay的根
\(link\):把两个点连边
把 \(x\) 弄到根节点 然后直接连即可
如果不保证合法需要判一下连之前是否就已经联通
void link(int x, int y) { //连一条x到y的边
makeroot(x);
if (findroot(y) == x) return; //如果x和y已经联通 那么就不要连边
fa[x] = y;
}
\(cut\):把两个点断边
把 \(x\) 弄到根节点 那么此时 \(x\) 与 \(y\) 如果联通 那么深度只会差 \(1\) 所以一定是 \(x\) 的儿子
然后双向断边即可
同样如果不保证合法需要特判
void cut(int x, int y) { //把x到y的边断开
makeroot(x);
if (findroot(y) != x || fa[y] != x || son[y][0]) return; //没联通/没有直接连边
fa[y] = son[x][1] = 0; //双向断边
update(x);
}
完整代码
P3690 【模板】动态树(LCT)的代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int n, m;
struct tree {
int fa[N], son[N][2], v[N], tr[N], st[N]; //st是等会要用的栈
bool lazy[N];
inline void update(int x) {
tr[x] = tr[son[x][0]] ^ tr[son[x][1]] ^ v[x];
}
inline void reverse(int x) { //左右儿子翻转
swap(son[x][0], son[x][1]);
lazy[x] ^= 1;
}
inline void pushdown(int x) {
if (lazy[x]) {
if (son[x][0]) reverse(son[x][0]);
if (son[x][1]) reverse(son[x][1]);
lazy[x] = 0;
}
}
inline bool get(int x) {
return x == son[fa[x]][1];
}
inline bool isroot(int x) { //查询x是不是一棵splay的根
return son[fa[x]][0] != x && son[fa[x]][1] != x;
}
void rotate(int x) {
int f = fa[x], gfa = fa[f];
bool i = get(x), i_ = get(f);
fa[x] = gfa;
if (!isroot(f)) son[gfa][i_] = x; //这地方变了 如果f是根就没有祖父 不要连 不然会连到别的splay上
son[f][i] = son[x][i ^ 1]; //而且一定要先写gfa那些东西 不然你底下改了f的父亲再判isroot就寄了
fa[son[x][i ^ 1]] = f;
son[x][i ^ 1] = f;
fa[f] = x;
update(x);
update(f);
}
void splay(int x) {
int tmp = x, top = 0;
st[++top] = x;
while (!isroot(tmp)) {
tmp = fa[tmp];
st[++top] = tmp;
}
for (int i = top; i; --i) pushdown(st[i]); //开一个栈把需要下传的节点都记录 然后从上往下下传
while (!isroot(x)) {
int f = fa[x];
if (!isroot(f)) {
if (get(f) == get(x)) rotate(f);
else rotate(x);
}
rotate(x);
}
update(x);
}
void access(int x) { //把x与根节点的边都连成实边
for (int y = 0; x; y = x, x = fa[x]) {
splay(x);
son[x][1] = y; //实际上是先让它等于0 然后连x 直接一步到位就行了
update(x);
}
}
void makeroot(int x) { //令x成为根节点
access(x);
splay(x); //此时x在splay的根节点
reverse(x); //access的时候x就是这条实链深度最深的点 所以在splay中x只有左儿子 把它们都翻转x就只有右儿子 此时就是这条链深度最浅的点 即为根节点
}
int findroot(int x) { //查询x所在那条链的根节点
access(x);
splay(x);
while (son[x][0]) pushdown(x), x = son[x][0]; //一直往左走
splay(x); //保证复杂度
return x;
}
void split(int x, int y) { //把x到y的路径拉出来
makeroot(x); //让x成为根
access(y); //把x到y拉出来
splay(y); //保证复杂度
}
void link(int x, int y) { //连一条x到y的边
makeroot(x);
if (findroot(y) == x) return; //如果x和y已经联通 那么就不要连边
fa[x] = y;
}
void cut(int x, int y) { //把x到y的边断开
makeroot(x);
if (findroot(y) != x || fa[y] != x || son[y][0]) return; //没联通/没有直接连边
fa[y] = son[x][1] = 0; //双向断边
update(x);
}
} LCT;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
scanf("%d", &LCT.v[i]);
LCT.update(i);
}
while (m--) {
int opt, x, y;
scanf("%d%d%d", &opt, &x, &y);
switch (opt) {
case 0 :
LCT.split(x, y);
printf("%d\n", LCT.tr[y]); //因为有个splay 此时y是splay的根
break;
case 1 :
LCT.link(x, y);
break;
case 2 :
LCT.cut(x, y);
break;
default :
LCT.splay(x); //先选上来再改
LCT.v[x] = y;
break;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号