2023.7.21 NOIP模拟赛 最终回
说句题外话 今天是我写
const int N = 1e5 + 0721;
最理直气壮的一天
然后恭喜混 100 计划在仅剩的最后一次机会圆满成功!!!!!!
赛时记录
HL最后一场模拟赛 给我冲!!!!
时间:7:30 - 12:00 考试时长:4.5h
开题
A.非常好题目 但是我好像忘了重心是啥 沙沙我错了
B.看起来可做 又不是很可做 很神秘
C.没看懂
D.看起来也可做点 也不是很可做
回去做A吧
A是不是向量可做啊 感谢沙沙((
\(30pts\) 解决
我们现在知道了重心的坐标表达式 我们写出来再推一下看性质
推完了 发现这玩意我好像学过 沙沙我错了
发现样例挺勾的 有机会建议拍一个
8:01 样例怎么炸了啊/fn 但是小样例过了 写个拍稳一下
等会 这玩意好像没法拍 坐标可能取到分数 那没办法了(悲
但是显然 用 40min 来 solve T1 对于这场的签到题而言是没什么优势的 没劣势就不错了
所以后面的题任重道远
B题首先有个很一眼的dp式 但是只能过 \(30pts\)
但是可以先敲 毕竟可以用来拍
稍微处理下发现可以做到 \(50pts\)
然后打了个表 发现了一些规律 但不明显
感觉还是不太好推 去写D题的 \(20pts\)
还剩3个小时 D的 \(20pts\) 敲完 发现我 T1 没开 long long 吓不吓死个人...
C还是没什么头绪 决定先冲B题正解
突然发现D的 \(30pts\) 可以直接预处理 但是要 \(O(1)\) 查询 先考虑不做
诶不对 离线 \(O(n ^ 2)\) 可做
还有2h40min 这下真冲T2正解去了
感觉C的那 \(50pts\) 应该是区间 \(DP\) 我感觉T2写完正解应该还有时间
算了 先拍D的 \(50pts\) 我挂不起
9:45 发现sqrt()因为 \(double\) 的精度问题寄了 那没辙了 做C吧
还剩2h 发现B的正解和C的 \(50pts\) 都没啥思路 不要放弃
10:13 通过观察 \(f\) 数组 发现可以按照平方进行分块
并且 \(10^{18}\) 是可以二分查的 那应该就切掉了 开码
10:35 大样例过了 拍一下
10:43 应该是没啥问题了 现在只剩两个选择 写C的部分分和D的正解 傻子都知道怎么选
10:55 A题突然发现一个事 要求必须是存在三角形是吧?
发现特判很寄 纯纯阴间毒瘤题
11:30 写了 \(inf\) 个特判 感觉还是能 \(hack\) 掉 寄寄寄
真没办法了 就这样吧(大悲
预计:\(\left[0, 100\right]\) + 100 + 0 + 50
实际:100 + 100 + 0 + 50 rk2

留个念
结果发现T1完全没卡不存在三角形的情况啊!!
附T2 T4珍贵对拍记录
赛后总结
七场名次变化:\(14 \rightarrow 15 \rightarrow 8 \rightarrow 17 \rightarrow 16 \rightarrow 17 \rightarrow 2\)
这次是我两次来HL模拟赛排名最高的一次 作为最后一场也算是圆满了
之前要么不会要么挂大分 在过去的三周多少次怀疑自己是否真的适合学 oi
这次想着最后一次模拟 忍住没去听歌没去扣键盘
虽然这可能只是一次偶然 但是对我来说已经足够
想说的大概就是
永远充满信心 永远小心谨慎 永远不要放弃 永远相信越认真越幸运
补题
A.
高一数学 设三角形三个顶点坐标是 \((x_1, y_1)\) \((x_2, y_2)\) \((x_3, y_3)\)
重心坐标就是 \((\frac{1}{3}(x_1 + x_2 + x_3), \frac{1}{3}(y_1 + y_2 + y_3))\)
(我是用向量导的 咋导能写出来就行)
然后就转化为了 给你三个顶点横纵坐标的取值范围 问它们的和加起来除以 \(3\) 那个范围包不包括给定点就行了
然后反正是和嘛 不等式直接加就完了
贴的是后面一车特判的代码 实际上只要 \(if\) 那行四个条件满足直接输出就能过
code:
#include <bits/stdc++.h>
#define ll long long
#define x1 x_1
#define y1 y_1
#define x2 x_2
#define y2 y_2
using namespace std;
const int N = 4;
ll x1, x2, y1, y2;
ll x, y;
int T;
struct node {
int xy[4];
};
node a, b, c, d;
bool check(node xx, node yy) {
bool flag = 1;
if (xx.xy[1] == xx.xy[2] && yy.xy[1] == yy.xy[2]) flag = 0;
if (xx.xy[2] == xx.xy[3] && yy.xy[2] == yy.xy[3]) flag = 0;
if (xx.xy[1] == xx.xy[3] && yy.xy[1] == yy.xy[3]) flag = 0;
return flag;
}
bool check2(bool flag) {
bool fl = 1;
if (flag) {
if (a.xy[1] == c.xy[1] && a.xy[2] == c.xy[2] && a.xy[1] == a.xy[2]) fl = 0;
if (a.xy[1] == c.xy[1] && a.xy[3] == c.xy[3] && a.xy[1] == a.xy[3]) fl = 0;
if (a.xy[2] == c.xy[2] && a.xy[3] == c.xy[3] && a.xy[3] == a.xy[2]) fl = 0;
} else {
if (b.xy[1] == d.xy[1] && b.xy[2] == d.xy[2] && b.xy[1] == b.xy[2]) fl = 0;
if (b.xy[1] == d.xy[1] && b.xy[3] == d.xy[3] && b.xy[1] == b.xy[3]) fl = 0;
if (b.xy[2] == d.xy[2] && b.xy[3] == d.xy[3] && b.xy[3] == b.xy[2]) fl = 0;
}
return fl;
}
bool check3(int x, int y) {
bool flag = 1;
if (a.xy[x] == c.xy[x] && a.xy[y] == c.xy[y] && b.xy[x] == d.xy[x] && b.xy[y] == d.xy[y] && a.xy[x] == a.xy[y] && b.xy[y] == b.xy[x]) flag = 0;
// cout << x <<" " << y << " " << flag << "\n";
return flag;
}
bool check4(int x) {
return a.xy[x] == c.xy[x] && b.xy[x] == d.xy[x];
}
int main() {
// freopen("gnsi1.in", "r", stdin);
scanf("%d", &T);
while (T--) {
x1 = x2 = y1 = y2 = 0;
for (int i = 1; i <= 3; ++i) {
scanf("%d%d%d%d", &a.xy[i], &c.xy[i], &b.xy[i], &d.xy[i]);
x1 += a.xy[i];
x2 += c.xy[i];
y1 += b.xy[i];
y2 += d.xy[i];
}
scanf("%lld%lld", &x, &y);
x *= 3;
y *= 3;
// cout << x1 << " " << x2 << " " << y1 << " " << y2 << " " << x << " " << y << "\n";
bool flag = 1;
if (x >= x1 && x <= x2 && y >= y1 && y <= y2) { //就这 直接输出就行 不用特判
if (x == x1 && y == y1) {
if (!check(a, b)) flag = 0;
}
else if (x == x2 && y == y1) {
if (!check(b, c)) flag = 0;
}
else if (x == x1 && y == y2) {
if (!check(a, d)) flag = 0;
}
else if (x == x2 && y == y2) {
if (!check(c, d)) flag = 0;
}
else if (x == x1 || x == x2) {
if (!check2(1)) flag = 0;
}
else if (y == y1 || y == y2) {
if (!check2(0)) flag = 0;
} else {
if (!check3(1, 2)) flag = 0;
if (!check3(2, 3)) flag = 0;
if (!check3(1, 3)) flag = 0;
}
if (check4(1) && check4(2) && check4(3)) {
if (a.xy[1] == x / 3 && b.xy[1] == y / 3) flag = 0;
if (a.xy[2] == x / 3 && b.xy[2] == y / 3) flag = 0;
if (a.xy[3] == x / 3 && b.xy[3] == y / 3) flag = 0;
}
if (flag) printf("heihei\n");
else printf("yiyandingzhen\n");
}
else printf("yiyandingzhen\n");
}
return 0;
}
/*
hack:
8
1 2 1 3
1 2 1 3
1 2 4 5
1 2
1 2 1 3
1 2 1 3
1 2 4 6
1 4
1 2 1 3
1 2 4 5
1 2 1 3
2 2
1 2 1 3
1 2 4 6
1 2 1 3
2 4
1 1 1 1
1 1 1 1
1 1 1 1
1 1
1 1 2 3
1 1 2 3
9 11 2 3
4 2
1 1 2 2
1 1 2 2
9 11 9 15
4 5
1 1 2 2
2 2 3 3
3 3 4 4
2 3
*/
B.
首先 \(114514\) 就是个幌子 因为裂到 \(1\) 后面就一样了
然后暴力的 \(DP\) 柿子挺一眼的 设 \(f_i\) 表示以 \(i\) 结尾列完有多少种可能
那么就有 \(f_n = \sum\limits_{i=1}^\sqrt{n} f_i\)
所以 \(10^9\) 的查询我们维护到 \(10^5\) 左右的前缀和就行了 \(50pts\)
考虑优化 我们把 \(f\) 数组打表打出来
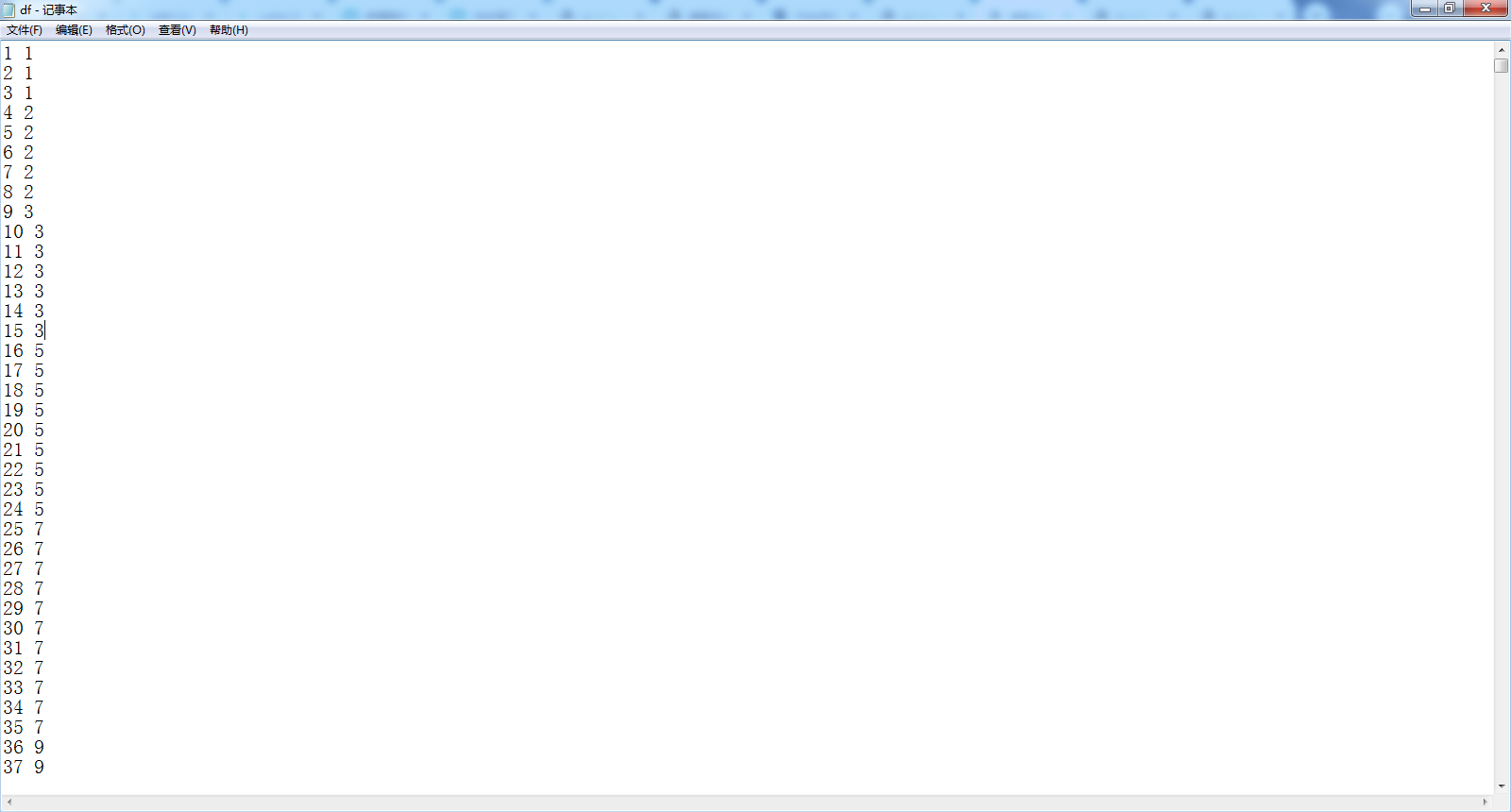
结合转移式 我们不难发现 只有 \(i\) 为完全平方数的时候 \(f_i\) 才会与 \(f_{i - 1}\) 不同
此时的 \(f_i = f_{i - 1} + f_{\sqrt{i}}\)
所以我们考虑对这 \(10^9\) 个 \(f_i\) 进行分块
\(B_i\) 表示 \(\left[i^2, (i + 1)^2 - 1\right]\) 这段区间
然后我们查一个前缀和的时候直接查询它在哪个块内 加上它到块头的距离和前 \(i - 1\) 个块的前缀和即可
因为询问是 \(10^{18}\) 级别 那么查询的前缀和就是 \(10^9\) 级别 再开个根号就存下了
code:
#include <bits/stdc++.h>
#define ll unsigned long long
#define int unsigned long long
using namespace std;
const int N = 32123;
const int mod = 998244353;
int T;
struct block {
ll val; //块里的元素大小
ll sum; //前缀和
ll l, r; //左右边界
} B[N];
int sq(ll val) { //手写的开平方
if (val == 0) return 0;
int l = 1, r = 1000000000;
int mid, ans;
while (l <= r) {
mid = (l + r) >> 1;
if (1ll * mid * mid <= val) {
ans = mid;
l = mid + 1;
} else
r = mid - 1;
}
return ans;
}
ll findf(ll x) { //查f值的
int id = sq(x);
return B[id].val;
}
ll find(ll x) { //查前缀和的
int id = sq(x);
// if (id <= 4) cout << x << " " << id << "\n";
ll ret = 0;
ret += B[id - 1].sum;
ret = (ret + (x - B[id].l + 1) * 1ll * B[id].val % mod) % mod;
return ret;
}
void init() {
B[1].val = 1;
B[1].l = 1;
B[1].r = 3;
B[1].sum = 3;
for (int i = 2; i <= 31623; ++i) {
B[i].val = (B[i - 1].val + findf(i)) % mod;
B[i].l = 1ll * i * i;
B[i].r = 1ll * (i + 1) * (i + 1) - 1;
B[i].sum = (B[i - 1].sum + B[i].val * (B[i].r - B[i].l + 1) % mod) % mod;
// if (i <= 10) cout << i << " " << B[i].val << "\n";
}
}
signed main() {
init();
scanf("%lld", &T);
// for (int i = 1; i <= 10; ++i) cout << findf(i) << " ";
while (T--) {
ll x;
scanf("%lld", &x);
int ss = sq(x);
printf("%lld\n", find(ss));
}
return 0;
}
/*
4
16
1
123456789012
1000000000000000000
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号