2023.7.19 NOIP模拟赛
今天早上上洛谷一打卡

别啊 我今天还要考模拟赛啊
赛时记录
开题
A.不就和昨天三元环一样吗
B.。。。
C.。。。。。
D.。。。。。。。
啥啊!!!!!!!!!!
8:25 发现不对 A题没那么简单
想到建反图有 \(40pts\) 但是怎么感觉样例不对劲啊。。
问了cdx 样例明白了 码吧
9:15 发现复杂度假了 加上发现D想到 \(50pts\) 状压也寄了 心态炸了
9:31 A题的 \(20pts\) 暴力敲完了 C看似 \(10pts\) 可写但是明显需要高精
D的状压需要记录前四行状态 先骗分
C就 \(10pts\) 还有坑啊
B破防了 本来就不知道转移式对不对还调不出来
没啥办法了 就这样吧
预计:20 + 0 + 10 + 30
实际:0 + 0 + 10 + 30
我T1没删freopen!!!!!!!
真爆了!!!!!!
赛后据说T1 \(O(nm)\) 的暴力有 \(85pts\) 早知道我去弄那个什么破反图干什么
补题
A.
反图想偏了 其实我们不用考虑判 \(u\) 不连通 \(v\)
实际上我们考虑把对于一个中间点 它能到达的所有点的贡献算出来
然后再减去三元环的贡献即可
这里算总贡献有个很好的方法:用和的平方减去平方之和
对于统计最大贡献 我们首先把每个点连的边按到达的那个点的点权从大到小排序
然后二重枚举 如果这两个点不构成一个三元环就 \(break\)
因为只有出现了三元环才会继续 所以这个操作次数和三元环的数量级相同 不会超时
code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 30721;
int w[N], u[N], v[N], deg[N], vis[N];
int n, m, t;
ll sum;
int maxn = -1;
struct node {
int id, val;
friend bool operator<(node x, node y) {
return x.val > y.val;
}
};
vector<node>v1[N], v2[N];
int main() {
scanf("%d%d%d", &n, &m, &t);
for (int i = 1; i <= m; ++i) scanf("%d%d", &u[i], &v[i]);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
for (int i = 1; i <= m; ++i) {
v1[u[i]].push_back((node){v[i], w[v[i]]});
v1[v[i]].push_back((node){u[i], w[u[i]]});
++deg[u[i]], ++deg[v[i]];
}
for (int i = 1; i <= n; ++i) {
ll tmp = 0;
for (int j = 0; j < v1[i].size(); ++j) {
sum -= v1[i][j].val * v1[i][j].val;
tmp += v1[i][j].val;
}
sum += tmp * tmp;
}
for (int i = 1; i <= m; ++i) {
if (deg[u[i]] > deg[v[i]] || deg[u[i]] == deg[v[i]] && u[i] > v[i]) swap(u[i], v[i]);
v2[u[i]].push_back((node){v[i], w[v[i]]});
}
memset(vis, 0, sizeof vis);
for (int x = 1; x <= n; ++x) {
for (int i = 0; i < v2[x].size(); ++i) vis[v2[x][i].id] = x;
for (int i = 0; i < v2[x].size(); ++i) {
int y = v2[x][i].id;
for (int j = 0; j < v2[y].size(); ++j) {
int z = v2[y][j].id;
if (vis[z] == x) {
sum -= 2 * (w[x] * w[y] + w[x] * w[z] + w[y] * w[z]);
// cout << x << " " << y << " " << z << "\n";
}
}
}
}
for (int i = 1; i <= n; ++i) sort(v1[i].begin(), v1[i].end());
for (int x = 1; x <= n; ++x) {
for (int i = 0; i < v1[x].size(); ++i) vis[v1[x][i].id] = x;
for (int i = 0; i < v1[x].size(); ++i) {
int y = v1[x][i].id;
for (int j = 0; j < v1[y].size(); ++j) {
int z = v1[y][j].id;
if (vis[z] != x && z != x) {
maxn = max(maxn, w[z] * w[x]);
// cout << x << " " << z << "\n";
break;
}
}
}
}
printf("%d\n%lld", t != 2 ? maxn : 0, t != 1 ? sum : 0);
return 0;
}
/*
4 4 3
1 2
1 3
2 3
2 4
100 1 100 1
*/
B.
首先转移式应该不难想 设 \(f_i\) 表示大小为 \(i\) 的树这一层期望节点数量 \(g _i\) 表示节点总数
那么我们有
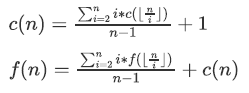
然后这个东西是可以整除分块的 加上记忆化搜索复杂度就会变成杜教筛那样的(我也不会证)
就可以把这题过掉了
另外注意这题数组下标会到 \(10^9\) 所以要开 \(unordered_map\) 映射一下
code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 998244353;
int n;
unordered_map<int, ll> f, g;
ll ksm(int x, int y) {
ll ret = 1;
while (y) {
if (y & 1) ret = ret * x % mod;
x = 1ll * x * x % mod;
y >>= 1;
}
return ret;
}
pair<ll, ll> dfs(int x) {
if (x == 1) return {1, 1};
if (f.find(x) != f.end()) return {f[x], g[x]};
ll inv = ksm(x - 1, mod - 2);
for (int l = 2, r; l <= x; l = r + 1) {
r = x / (x / l); auto tmp = dfs(x / l);
f[x] = (f[x] + 1ll * (r + l) * (r - l + 1) / 2 % mod * tmp.first % mod) % mod; //因为是分块算的 所以算的时候把l到r都加一起
g[x] = (g[x] + 1ll * (r + l) * (r - l + 1) / 2 % mod * tmp.second % mod) % mod;
}
f[x] = (f[x] * inv + 1) % mod;
g[x] = (g[x] * inv + f[x]) % mod;
return {f[x], g[x]};
}
int main() {
scanf("%d", &n);
cout << dfs(n).second;
return 0;
}
C.
我们设 \(f_{n, m}\) 表示把 \(n\) 个用 \(m\) 阶汉诺塔做的次数
那么我们枚举 \(k\) 把上面的 \(k\) 个都移到一个柱子上
然后把剩下的 \(n - k\) 个用 \(m - 1\) 个柱子移到头
然后把那 \(k\) 个移到头
那么就有
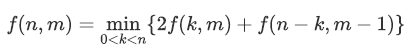
据说用 \(int128\) 可以存下
分析可以看出 \(k\) 是具有单调性的 所以我们可以用类似双指针的东西省略对 \(k\) 的枚举
具体看代码吧 我也解释不明白(
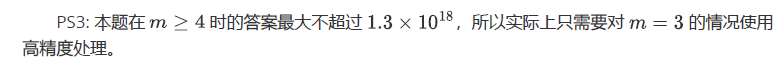
code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1507;
int T, m, n;
ll dp[N][N];
struct num {
int len;
int wei[521];
friend num operator+(num x, num y) {
num ret;
int maxlen = max(x.len, y.len);
for (int i = 1; i <= maxlen + 1; ++i) ret.wei[i] = 0;
for (int i = 1; i <= maxlen; ++i) ret.wei[i] = x.wei[i] + y.wei[i];
for (int i = 1; i <= maxlen; ++i) {
ret.wei[i + 1] += ret.wei[i] / 10;
ret.wei[i] %= 10;
}
ret.len = ret.wei[maxlen + 1] ? maxlen + 1 : maxlen;
return ret;
}
};
num f[N];
void print(num x) {
for (int i = x.len; i >= 1; --i) printf("%d", x.wei[i]);
printf("\n");
}
void init() {
for (int i = 2; i <= 1500; ++i) {
f[i] = f[i - 1] + f[1];
f[i] = f[i] + f[i - 1];
}
}
void init2() {
memset(dp, 0x3f, sizeof dp);
for (int i = 0; i <= 1500; ++i) dp[0][i] = 0;
dp[1][2] = 1;
for (int j = 3; j <= 1500; ++j) {
int k = 0;
for (int i = 1; i <= 1500; ++i) {
while (1) {
dp[i][j] = 2 * dp[k][j] + dp[i - k][j - 1];
if (i > k && 2 * dp[k + 1][j] + dp[i - k - 1][j - 1] < dp[i][j]) {
++k;
dp[i][j] = 2 * dp[k][j] + dp[i - k][j - 1];
} else
break;
}
}
}
}
int main() {
scanf("%d", &T);
f[1].len = 1;
f[1].wei[1] = 1;
init();
init2();
while (T--) { //由赛时代码修改而来 看起来可能有点怪
scanf("%d%d", &n, &m);
if (m == 1) printf("0\n");
else if (m == 2) {
n == 1 ? printf("1\n") : printf("No Solution\n");
} else if (m == 3) print(f[n]);
else printf("%lld\n", dp[n][m]);
}
return 0;
}
D.
cdx看这题说一眼秒了 就是下五子棋有个民间八卦阵可以让对方永远不赢
大概长这样:

然后我们用这玩意把 \(505 * 505\) 的正方形都铺满
然后我们枚举最左上角的 \(5 * 5\) 那 \(25\) 个格作为我要放整张雷图左上角那个点
然后就做完了
code:
#include <bits/stdc++.h>
#define x1 x_1
#define x2 x_2
#define y1 y_1
#define y2 y_2
using namespace std;
const int N = 521;
int f[N][N], st[5] = { 0, 2, 4, 1, 3 };
int n, m;
int minn = 0x7fffffff;
int cal(int x1, int y1, int x2, int y2) {
int res = 0;
for (int i = x1; i <= x2; ++i) {
for (int j = y1; j <= y2; ++j) res += f[i][j];
}
return res;
}
void print(int x1, int y1, int x2, int y2) {
for (int i = x1; i <= x2; ++i) {
for (int j = y1; j <= y2; ++j) printf("%d", f[i][j]);
printf("\n");
}
exit(0);
}
int main() {
for (int i = 0; i < N; ++i) {
for (int j = st[i % 5]; j < N; j += 5) f[i][j] = 1; //先把八卦阵填好
}
scanf("%d%d", &n, &m);
for (int i = 0; i < 5 && i < n; ++i) {
for (int j = 0; j < 5 && j < m; ++j) minn = min(minn, cal(i, j, i + n - 1, j + m - 1)); //枚举这个矩形在八卦阵中的左上角位置
}
printf("%d\n", minn);
for (int i = 0; i < 5 && i < n; ++i) {
for (int j = 0; j < 5 && j < m; ++j) {
if (cal(i, j, i + n - 1, j + m - 1) == minn) print(i, j, i + n - 1, j + m - 1);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号