2023.7.11 NOIP模拟赛
破防了 混个 100 怎么这么难
赛时记录
A 没看懂 难绷
B 没思路
C 什么是割 直接放吧
D 看懂了 但是好难
A后来附加了解释 终于看懂了 但还是很懵
看到数据范围应该是 \(O(n)\) 的 那每一项要么是单独 \(O(1)\) 要么是递推 应该是后者
那么我们考虑 \(i\) 插入对 \(i - 1\) 的影响
9:26 70pts的 \(O(n^2)\) 想出来了 但是希望别挂
9:44 写完了 熟悉的大样例寄掉了
9:45 大样例调过了!!!
D猜测正解或者说很大部分的部分分和运输计划很像 二分答案+树上差分
但是我的评价是我能码出来 \(O(n ^ 2 logn)\) 那个就不错了
结果一顿捣鼓发现我靠假了 是 \(O(n ^ 3 logn)\) 很寄
10:33 码完了 大样例又双叒叕寄了
发现链不只是从上到下的 开摆!
改完了 然后调不出来了 还是捆测 我谔谔
又改完了 但是不知道为啥 T 了
怄火 恼怒 转圈 怄火 恼怒 转圈 怄火 恼怒 转圈 怄火 恼怒 转圈 怄火 恼怒 转圈 怄火 恼怒 转圈 怄火 恼怒 转圈 怄火 恼怒 转圈
破防了 为什么我这么菜 破防了 为什么我这么菜 破防了 为什么我这么菜 破防了 为什么我这么菜 破防了 为什么我这么菜 破防了 为什么我这么菜
预计:70 + 0 + 0 + 0
实际:70 + 0 + 0 + 0 rk8
补:
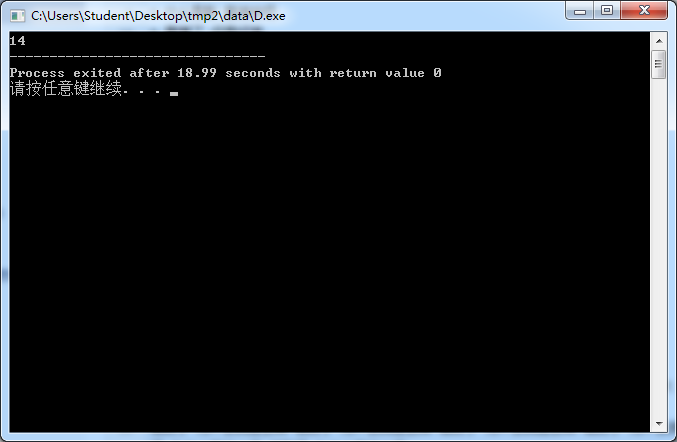
upd:吸了八聚氧变成了 14.36s 但还是没什么卵用
补题
A.
这里先贴一下 \(70pts\) 的赛时代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 0721;
ll f[N], fac[N], c[N][2], v[N];
int k;
ll inv, ans;
ll mod;
int n;
ll ksm(ll x, ll y) {
ll ret = 1;
while (y) {
if (y & 1) ret = ret * x % mod;
x = x * x % mod;
y >>= 1;
}
return ret;
}
void init() {
fac[0] = fac[1] = 1;
for (int i = 2; i <= n; ++i) fac[i] = fac[i - 1] * i % mod;
}
void dp(int m) {
k = k ^ 1;
for (int i = 1; i <= m; ++i) c[i][k] = (c[i - 1][k ^ 1] + c[i + 1][k ^ 1] * (i + 1) % mod) % mod;
c[0][k] = c[1][k ^ 1];
ll sum = 0;
for (int i = 0; i <= m; ++i) sum = (sum + ((i + 1) * c[i][k]) % mod) % mod;
v[m] = ((fac[m + 1] - sum) % mod + mod) * inv % mod;
ans ^= v[m];
}
int main() {
scanf("%d%lld", &n, &mod);
c[0][k] = 1;
inv = ksm(2, mod - 2);
init();
for (int i = 1; i < n; ++i) dp(i);
printf("%lld", ans);
return 0;
}
主要是这段讲起来很麻烦想起来也挺麻烦所以就摆了
后面其实偏了 主要是过分注意转移差值发现柿子错了
实际上我们观察一下这个图
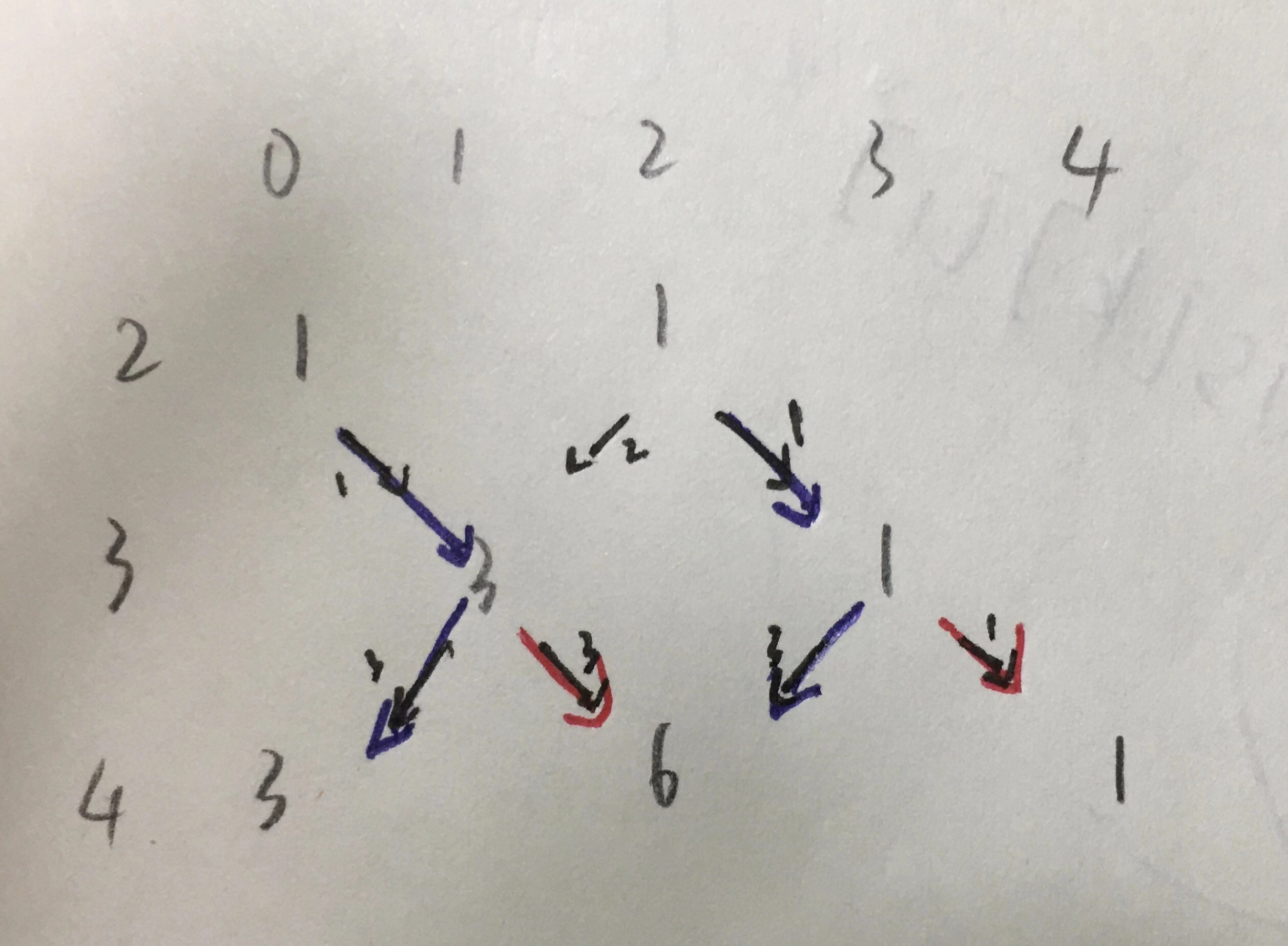
发现红色其实就是 \(f_{i - 1}\)
蓝色就是把 \(f_2\) 乘了 \(3\) 倍
那如果继续画下去 画到第五个 其实转移式就出来了
\(f_i = f_{i - 1} * f_{i - 2} * (i - 1)\)
没错 就是这么简单的一个玩意(吐血)
code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e7 + 0721;
ll f[N], fac[N], v[N];
int k;
ll inv, ans;
ll mod;
int n;
ll ksm(ll x, ll y) {
ll ret = 1;
while (y) {
if (y & 1) ret = ret * x % mod;
x = x * x % mod;
y >>= 1;
}
return ret;
}
void init() {
fac[0] = fac[1] = 1;
for (int i = 2; i <= n; ++i) fac[i] = fac[i - 1] * i % mod;
}
void dp(int m) {
f[m] = (f[m - 1] + f[m - 2] * (m - 1) % mod) % mod;
v[m] = ((fac[m] - f[m]) % mod + mod) * inv % mod;
ans ^= v[m];
}
int main() {
// freopen("ex_perm1.in", "r", stdin);
scanf("%d%lld", &n, &mod);
f[0] = f[1] = 1;
inv = ksm(2, mod - 2);
init();
for (int i = 2; i <= n; ++i) dp(i);
printf("%lld", ans);
return 0;
}
B.
与我也忘了昨天的哪道题一样 我们算贡献
即计算当这个最大值为 \(k\) 的时候的染色方案数 乘起来就是对应的贡献
首先这题要求的是两点间最大距离 考虑直径
如果直径的两个端点同色 那么别的点怎么染色都行
我们考虑直径的两个端点不同的情况 考虑此时两同色点之间的最距离为 \(k\)
那么对于一个点而言 与它距离的最大值点一定出现在直径的两个端点
那么如果假如说这个点到那个黑端点的距离为 \(d\) 并且 \(d > k\) 那么这个点就只能是白的
反过来也是同理的
如果这个点到两个端点的距离都不超过 \(k\) 那它就是涂什么颜色都可以的
如果到两个端点的距离都大于 \(k\) 那就没有合法方案数了 并且更小的 \(k\) 也没有合法方案数了
所以我们从直径的两个端点做一边 \(dfs\) 维护这个距离即可
\(std\) 统计答案的时候用了一种很新的写法
code:
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
const int N = 1e6 + 0721;
int x1, x2;
int head[N], nxt[N << 2], to[N << 2], cnt;
int dis[N];
int c[N];
bool vis[N];
int n, ans;
struct node {
int dis1, dis2;
} a[N];
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
int ksm(int x, int y) {
int ret = 1;
while (y) {
if (y & 1) ret = 1ll * ret * x % mod;
x = 1ll * x * x % mod;
y >>= 1;
}
return ret;
}
void dfs(int x, int fa) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
dis[y] = dis[x] + 1;
dfs(y, x);
}
}
void dfs1(int x, int fa) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
a[y].dis1 = a[x].dis1 + 1;
dfs1(y, x);
}
}
void dfs2(int x, int fa) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
a[y].dis2 = a[x].dis2 + 1;
dfs2(y, x);
}
}
void find_d() {
dfs(1, 0);
for (int i = 1; i <= n; ++i) if (dis[i] > dis[x1]) x1 = i;
dis[x1] = 0;
dfs(x1, 0);
for (int i = 1; i <= n; ++i) if (dis[i] > dis[x2]) x2 = i;
}
void find_dis() {
dfs1(x1, 0);
dfs2(x2, 0);
}
void solve() { //就这块
int maxn = dis[x2];
int sum = ksm(2, n);
int num = n + 1;
for (int i = maxn; i >= 0; --i) {
if (vis[i]) {
ans = (ans + 1ll * i * sum % mod) % mod;
printf("%d", ans);
return;
}
num -= c[i];
int tmp = ksm(2, num);
ans = (ans + 1ll * i * (sum - tmp + mod) % mod) % mod;
sum = tmp;
}
}
int main() {
// freopen("ex_tree2.in", "r", stdin);
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
add_edge(x, y);
add_edge(y, x);
}
find_d();
find_dis();
for (int i = 1; i <= n; ++i) {
++c[a[i].dis1];
++c[a[i].dis2];
vis[min(a[i].dis1, a[i].dis2)] = 1;
}
solve();
return 0;
}
C.
这题。。。你想到了就想到了 想不到就没办法了
首先对于一个图的 \(k\) 度子图 它一定是不相交的一坨一坨一坨
因为如果相交 那么两个相交的一坨会构成一坨更大的 \(k\) 度子图
然后我们考虑枚举 \(k\) 并把此时的答案算出来
那么我们发现这个图中所有度数小于 \(k\) 的点都会被删掉
所以我们先把这些点都删掉 然后把与它相邻的点也减一下度数
然后考虑 因为我们要枚举 \(k\) 我们显然要求出每个 \(k\) 图中的联通情况 或者说删了哪些点
然后我们发现 显然 \(k\) 越大 删掉的点就越多
并且当 \(k = i\) 时 删的点一定是基于 \(k = i - 1\) 那张图的基础上的
所以我们记录下当前 \(k\) 新删的点就可以了
最后统计的时候我们倒过来加点 然后用并查集维护
这个求割也是一种很新的方式
code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e6 + 0721;
int v[maxn], e[maxn], d[maxn]; //点数 边数 deg
int deg[maxn], fa[maxn];
int head[maxn], nxt[maxn << 2], to[maxn << 2], cnt;
vector<int> q[maxn];
bool vis[maxn], exist[maxn];
int M, N, B;
int n, m;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y) {
int fx = find(x), fy = find(y);
++e[fx];
if (fx == fy) return;
d[fx] += d[fy];
e[fx] += e[fy];
v[fx] += v[fy];
fa[fy] = fx;
}
ll calc(int x) {
int fx = find(x);
return 1ll * M * e[fx] - 1ll * N * v[fx] + 1ll * B * (d[fx] - (e[fx] << 1));
}
int main() {
// freopen("ex_data2.in", "r", stdin);
scanf("%d%d", &n, &m);
scanf("%d%d%d", &M, &N, &B);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
add_edge(x, y);
add_edge(y, x);
++deg[x], ++deg[y];
}
for (int i = 1; i <= n; ++i) {
q[deg[i]].push_back(i);
d[i] = deg[i];
fa[i] = i;
v[i] = 1;
}
for (int i = 1; i <= n; ++i) {
int len = 0;
for (int j = 0; j < q[i].size(); ++j) {
int id = q[i][j];
if (vis[id]) continue;
q[i][len] = id;
++len;
vis[id] = 1;
for (int k = head[id]; k; k = nxt[k]) {
int y = to[k];
if (vis[y]) continue; //已经被删掉了
--deg[y];
q[max(i, deg[y])].push_back(y); //如果原来deg等于i或者删完是i 都要在这波删掉 等会循环到它的时候就会把它记录到
}
}
q[i].resize(len);
}
ll maxx = -0x7ffffffffffffff;
int ans;
for (int i = n; i >= 1; --i) {
for (int u : q[i]) {
exist[u] = 1; //把这个点还原
for (int j = head[u]; j; j = nxt[j]) {
int y = to[j];
if (exist[y]) merge(u, y); //如果这个点存在
}
}
for (int u : q[i]) {
ll val = calc(u);
if (val > maxx) {
maxx = val;
ans = i;
}
}
}
printf("%d %lld", ans, maxx);
return 0;
}
D.
不会长链剖分 看不懂题解 再说吧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号