平衡树之Splay
本篇中所有应该放图的地方都会空出来 等拿到手机会补
但是我真的都画完了你相信我
upd:补完了
前置知识:二叉查找树
首先我们要看一下二叉查找树
它满足这些性质:
1.它是二叉树(废话)
2.对于任何一个根节点 它左子树的所有点都小于它 它右子树的所有点都大于它
所以实际上它的中序遍历就是对整个序列排序的结果
它非常的方便 支持查询很多的东西(后面会讲)
但是如果只是普通的插入 很容易让它复杂度假掉 所以我们需要一些手段来维持它的平衡
这就是平衡树
Splay
首先是祖传的新建节点和更新
int son[N][2], cnt[N], siz[N], fa[N], val[N]; //左右儿子编号 是这个权值的数的数目 子树大小 父亲编号 权值
int root = 0, tot = 0;
int newnode(int x, int f) {
val[++tot] = x;
fa[tot] = f;
son[tot][0] = son[tot][1] = 0;
cnt[tot] = siz[tot] = 1;
return tot;
}
inline void maintain(int x) {
siz[x] = cnt[x] + siz[son[x][0]] + siz[son[x][1]];
}
此外 我们还需要一个查询它是父亲的哪个儿子的函数 等会会用到
inline bool get(int x) { //查询x是它父亲的哪个儿子
return x == son[fa[x]][1]; //压行小技巧 如果x是右儿子就返还1 否则返还0
}
Splay的核心就在于旋转操作
我们首先看一下假如说我要把一个点往上转会发生什么
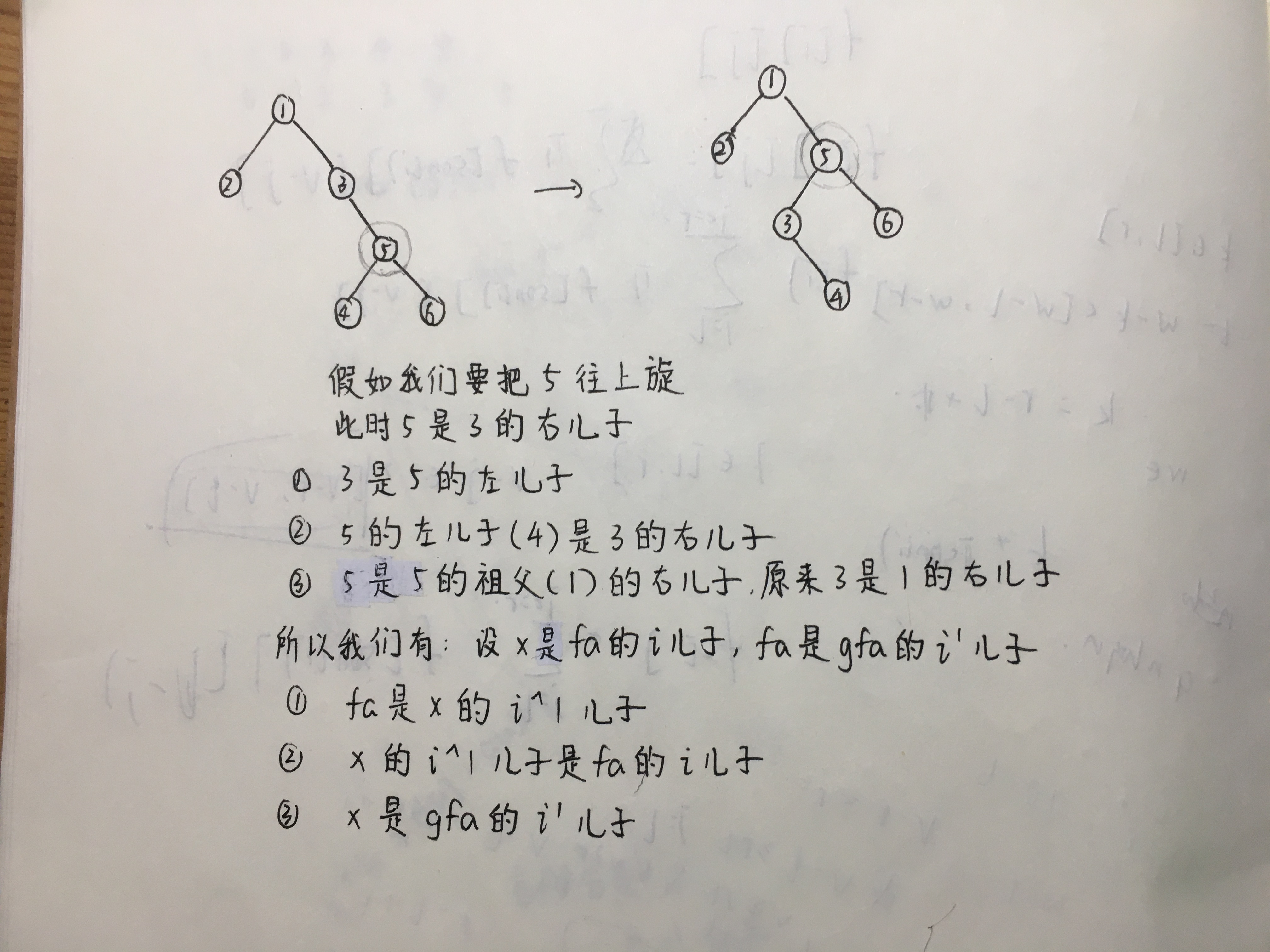
根据这个 我们可以写出以下代码
void rotate(int x) { //核心操作 将x往上旋
int f = fa[x], gfa = fa[f];
bool i = get(x), i_ = get(f);
son[f][i] = son[x][i ^ 1]; //x的i^1儿子是fa的i儿子 注意顺序不能反
fa[son[x][i ^ 1]] = f;
son[x][i ^ 1] = f; //x现在的i^1儿子是fa
fa[f] = x;
fa[x] = gfa;
if (gfa) son[gfa][i_] = x; //x是gfa的i'儿子
maintain(x);
maintain(f); //改一下x和f的大小 gfa就没必要改了
}
然后我们还需要一个 \(splay\) 操作 把编号为 \(x\) 的旋到根结点
这里我们有三种情况:
- \(x\) 的父亲就是根节点 那么 \(x\) 转一次就行
- \(x\) 和它的父亲 祖父三点共线 那么我们要先转父亲再转 \(x\)
- 否则 就把 \(x\) 转两次
这里解释一下第二条
因为我们 \(splay\) 的时候要顺便把路径上的链都消掉
如果我们先转儿子 就会出现以下情况
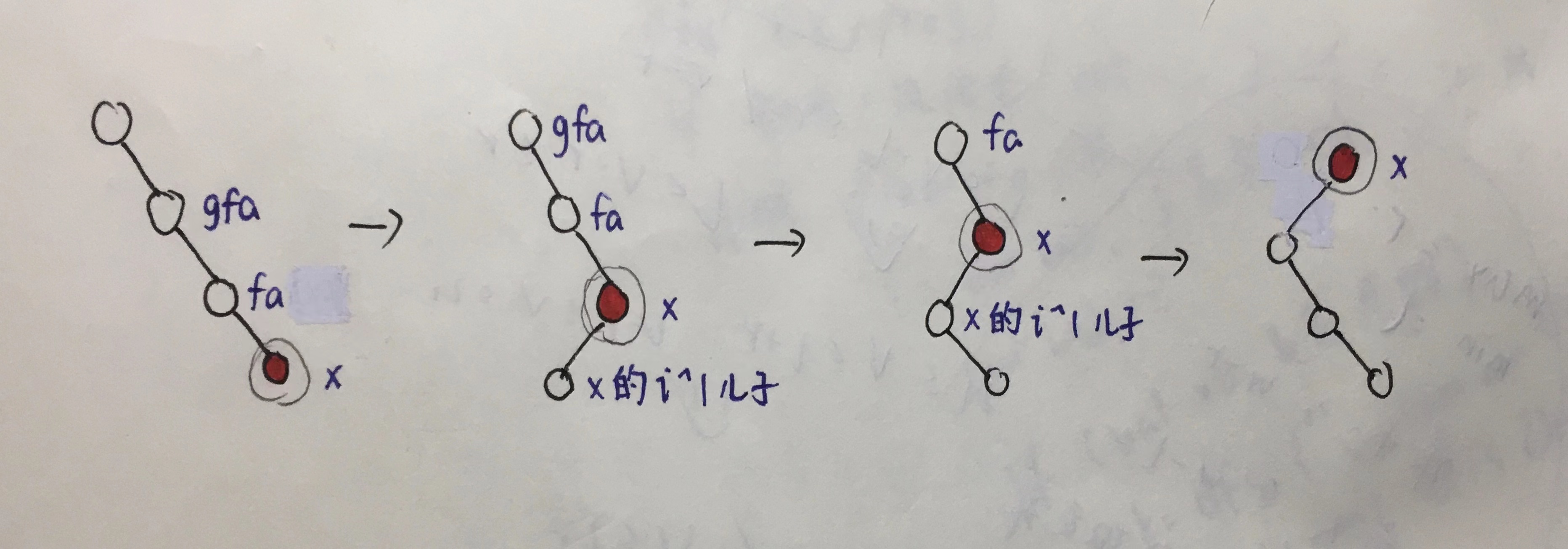
如果先转父亲 就可以使转完后路径上不存在链
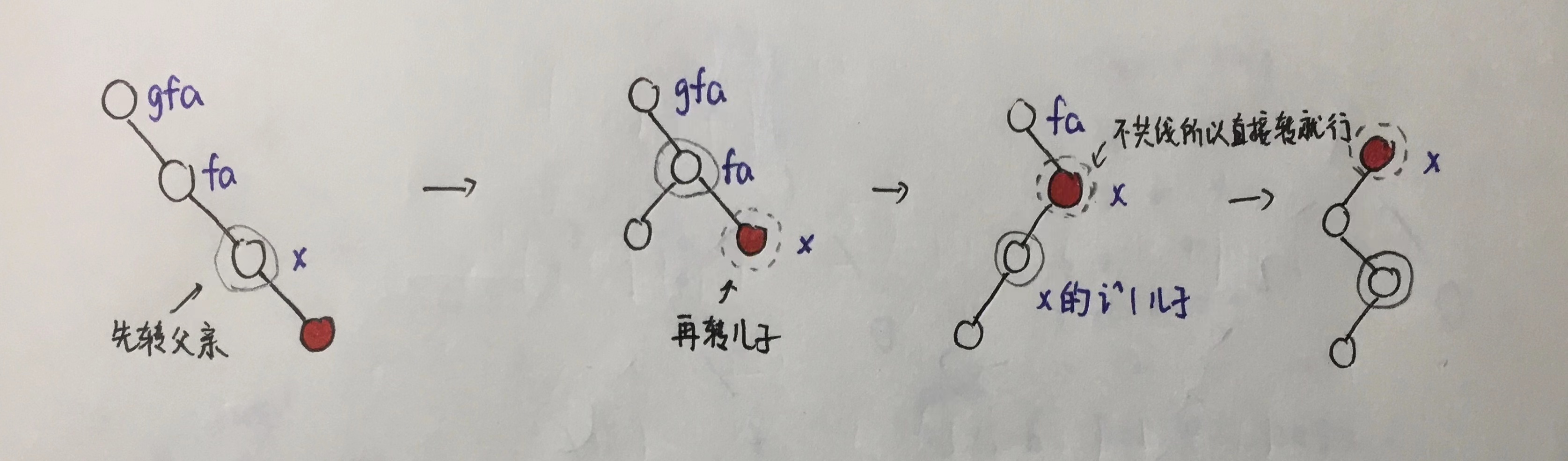
关于这个操作的复杂度我不会证 感兴趣的可以看看oi wiki
void splay(int x) { //把x旋到根
for (int f; f = fa[x]; rotate(x)) { //每次循环都转一次x
if (fa[f]) { //如果没有祖父在循环那转一次就行
if (get(f) == get(x)) rotate(f); //如果三点共线 第一次先转父亲 加上循环那次就是先转父亲再转x
else rotate(x); //否则 第一次转x 加上循环那次就是连续转两次x
}
}
root = x;
}
然后就是一些操作了
- insert
void insert(int x) { //插入一个权值为x的数
if (root == 0) { //没有根节点就把它当成根节点
root = newnode(x, 0);
return;
}
int now = root, f = 0;
while (1) {
if (val[now] == x) { //如果查到了这个权值对应的节点
++cnt[now];
maintain(now); //注意顺序不能反 先更新儿子再更新父亲
maintain(f);
splay(now);
return;
}
f = now;
now = son[now][x > val[now]]; //压行小技巧 如果当前权值大于x就说明在右子树里 不然在左子树里
if (!now) { //如果发现不存在这个权值对应的节点
now = newnode(x, f);
son[f][x > val[f]] = now; //还是那个压行小技巧
maintain(f);
splay(now);
return;
}
}
}
- kth
int kth(int x) { //查询排名为x的数
int now = root;
while (1) {
if (siz[son[now][0]] >= x) now = son[now][0]; //查过头了
else if (siz[son[now][0]] + cnt[now] >= x) return val[now]; //正好查到
else {
x -= (siz[son[now][0]] + cnt[now]);
now = son[now][1]; //没查够
}
}
}
- rank
int rank(int x) { //查询x的排名
int now = root, ans = 0;
while (1) {
if (!now) return ans + 1; //树中不存在这个数 那就是目前查到比它小的数的数目+1
if (val[now] > x) now = son[now][0]; //要查的数比now节点的数小 说明在左子树
else if (val[now] == x) {
ans += siz[son[now][0]]; //比它小的数的数目
splay(now);
return ans + 1;
} else { //要查的数在左子树
ans += siz[son[now][0]] + cnt[now]; //此时当前节点和左子树所有数都比它小
now = son[now][1];
}
}
}
- findpre / findnxt
int findpre() { //查询根节点的前驱对应的结点编号
int now = son[root][0]; //首先进入左子树 因为左子树的所有数都比它小
while (son[now][1]) now = son[now][1]; //然后一直往大的走 找最大的
return now;
}
int findnxt() { //跟上面同理
int now = son[root][1];
while (son[now][0]) now = son[now][0];
return now;
}
···
else if (opt == 5) {
splay.insert(x); //把x先旋到根节点 而且一定要插入而不是直接旋 防止树上本来就没有x
printf("%d\n", splay.val[splay.findpre()]);
splay.del(x); //用完删掉
} else {
splay.insert(x); //同上
printf("%d\n", splay.val[splay.findnxt()]);
splay.del(x);
}
- del
这个需要一些说明
首先我们用 rank 函数把权值为 \(x\) 的那个结点旋到根节点
那么会出现以下两种情况:
- 该点的 \(cnt > 1\) 那么就说明这个数不止一个 直接 \(--cnt\) 即可
- 该点的 \(cnt = 1\) 那么就说明要把这个点删掉
其中第二种情况可以继续细分:
- 它左右儿子都没有 那么整个树就被删光了
- 它左右儿子只有其中一个 那就让那个儿子成为新的根结点
- 它左右儿子都有
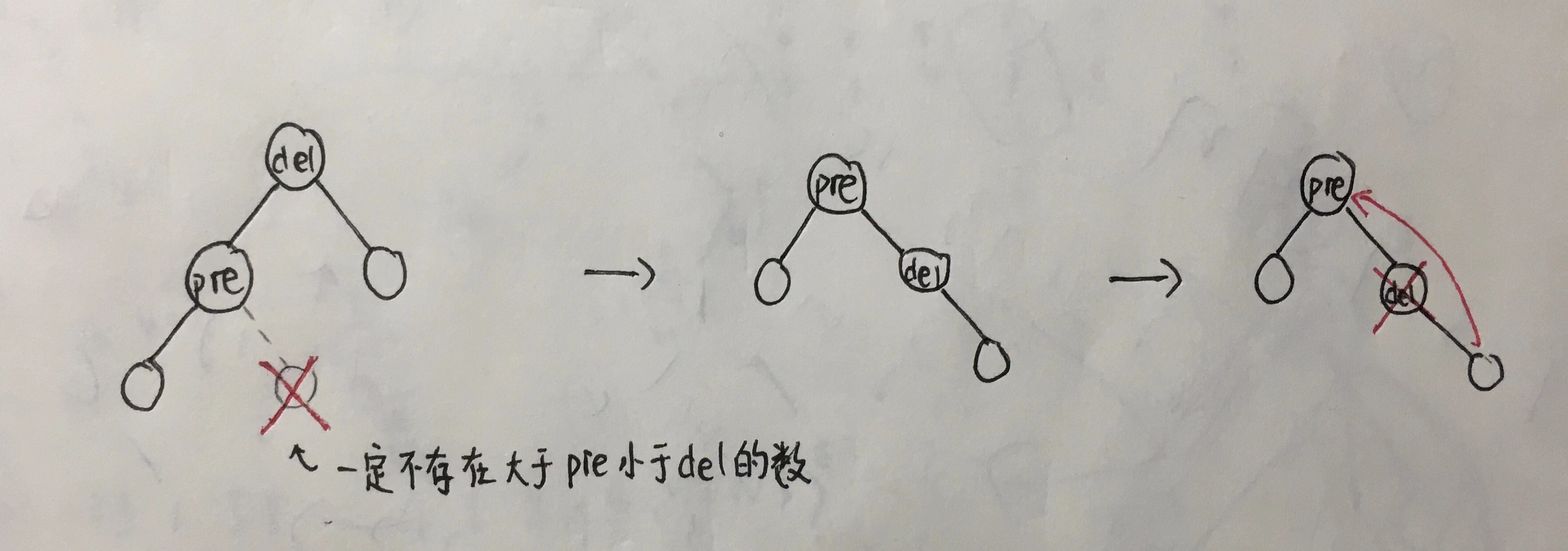
我们重点分析一下第三种情况:
我们首先利用 findpre 函数把 \(x\) 的前驱找到 此时该前驱一定在 \(x\) 的左子树里 并且该前驱一定没有右子树
然后我们把该前驱旋转到根节点 这样 \(x\) 就到了前驱的右子树里 并且 \(x\) 一定没有左子树
然后把 \(x\) 的右儿子直接连到根节点即可
void del(int x) { //删除大小为x的数
int _ = rank(x); //把代表x的结点旋到根节点
if (cnt[root] > 1) {
--cnt[root];
return;
} else if (son[root][0] == 0 && son[root][0]) { //左右儿子都没有 整个树就删光了
root = 0;
return;
} else if (son[root][0] == 0) { //只有右儿子
root = son[root][1];
fa[root] = 0;
} else if (son[root][1] == 0) { //只有左儿子
root = son[root][0];
fa[root] = 0;
} else { //左右儿子都有
int rs = son[root][1];
int pre = findpre(); //查询前驱
splay(pre); //把前驱旋到根
son[pre][1] = rs; //把原来的右儿子连到前驱上
fa[rs] = pre;
maintain(pre);
}
}
所以 splay 容易写挂的原因找到了 要是哪个 splay 和 maintain 忘写了就寄了
那么怎么记住到底哪要写哪不用写呢
对于 maintain 很简单 你改了啥就把它自己 maintain 一下 再把父亲(如果有)也 maintain 一下
对于 splay 实际上我们使用这个函数的同时如果要实现提根的功能 那就写
比如 insert 我们查询前驱后继需要使用它并且把插入的数旋到根 所以要写
比如 rank 我们就是要用它把权值为 \(x\) 的结点旋到根节点 所以要写
再比如 del 呃这个你肯定不能忘
如果还记不住怎么办呢
首先我们要明确 splay 是复杂度的保证 写少了复杂度就会假
但是你多写几个肯定是没事的
maintain 也是 如果你该更新的没更新肯定就寄了
但是你把没必要更新的也更新了问题就不大
所以实在不行这俩就是能写就写
当然这么干常数就又会变大 所以最好还是记一下上面那个
最后附上P3369 【模板】普通平衡树的代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
const int inf = 0x7fffffff;
int n;
struct tree {
int son[N][2], cnt[N], siz[N], fa[N], val[N]; //左右儿子编号 是这个权值的数的数目 子树大小 父亲编号 权值
int root = 0, tot = 0;
int newnode(int x, int f) {
val[++tot] = x;
fa[tot] = f;
son[tot][0] = son[tot][1] = 0;
cnt[tot] = siz[tot] = 1;
return tot;
}
inline void maintain(int x) {
siz[x] = cnt[x] + siz[son[x][0]] + siz[son[x][1]];
}
inline bool get(int x) { //查询x是它父亲的哪个儿子
return x == son[fa[x]][1]; //压行小技巧 如果x是右儿子就返还1 否则返还0
}
void rotate(int x) { //核心操作 将x往上旋
int f = fa[x], gfa = fa[f];
bool i = get(x), i_ = get(f);
son[f][i] = son[x][i ^ 1]; //x的i^1儿子是fa的i儿子 注意顺序不能反
fa[son[x][i ^ 1]] = f;
son[x][i ^ 1] = f; //x现在的i^1儿子是fa
fa[f] = x;
fa[x] = gfa;
if (gfa) son[gfa][i_] = x; //x是gfa的i'儿子
maintain(x);
maintain(f); //改一下x和f的大小 gfa就没必要改了
}
void splay(int x) { //把x旋到根
for (int f; f = fa[x]; rotate(x)) { //每次循环都转一次x
if (fa[f]) { //如果没有祖父在循环那转一次就行
if (get(f) == get(x)) rotate(f); //如果三点共线 第一次先转父亲 加上循环那次就是先转父亲再转x
else rotate(x); //否则 第一次转x 加上循环那次就是连续转两次x
}
}
root = x;
}
void insert(int x) { //插入一个权值为x的数
if (root == 0) { //没有根节点就把它当成根节点
root = newnode(x, 0);
return;
}
int now = root, f = 0;
while (1) {
if (val[now] == x) { //如果查到了这个权值对应的节点
++cnt[now];
maintain(now); //注意顺序不能反 先更新儿子再更新父亲
maintain(f);
splay(now);
return;
}
f = now;
now = son[now][x > val[now]]; //压行小技巧 如果当前权值大于x就说明在右子树里 不然在左子树里
if (!now) { //如果发现不存在这个权值对应的节点
now = newnode(x, f);
son[f][x > val[f]] = now; //还是那个压行小技巧
maintain(f);
splay(now);
return;
}
}
}
int kth(int x) { //查询排名为x的数
int now = root;
while (1) {
if (siz[son[now][0]] >= x) now = son[now][0]; //查过头了
else if (siz[son[now][0]] + cnt[now] >= x) return val[now]; //正好查到
else {
x -= (siz[son[now][0]] + cnt[now]);
now = son[now][1]; //没查够
}
}
}
int rank(int x) { //查询x的排名
int now = root, ans = 0;
while (1) {
if (!now) return ans + 1; //树中不存在这个数 那就是目前查到比它小的数的数目+1
if (val[now] > x) now = son[now][0]; //要查的数比now节点的数小 说明在左子树
else if (val[now] == x) {
ans += siz[son[now][0]]; //比它小的数的数目
splay(now);
return ans + 1;
} else { //要查的数在左子树
ans += siz[son[now][0]] + cnt[now]; //此时当前节点和左子树所有数都比它小
now = son[now][1];
}
}
}
int findpre() { //查询根节点的前驱对应的结点编号
int now = son[root][0]; //首先进入左子树 因为左子树的所有数都比它小
while (son[now][1]) now = son[now][1]; //然后一直往大的走 找最大的
return now;
}
int findnxt() { //跟上面同理
int now = son[root][1];
while (son[now][0]) now = son[now][0];
return now;
}
void del(int x) { //删除大小为x的数
int _ = rank(x); //把代表x的结点旋到根节点
if (cnt[root] > 1) {
--cnt[root];
return;
} else if (son[root][0] == 0 && son[root][0]) { //左右儿子都没有 整个树就删光了
root = 0;
return;
} else if (son[root][0] == 0) { //只有右儿子
root = son[root][1];
fa[root] = 0;
} else if (son[root][1] == 0) { //只有左儿子
root = son[root][0];
fa[root] = 0;
} else { //左右儿子都有
int rs = son[root][1];
int pre = findpre(); //查询前驱
splay(pre); //把前驱旋到根
son[pre][1] = rs; //把原来的右儿子连到前驱上
fa[rs] = pre;
maintain(pre);
}
}
} splay;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int opt, x;
scanf("%d%d", &opt, &x);
if (opt == 1) splay.insert(x);
else if (opt == 2) splay.del(x);
else if (opt == 3) printf("%d\n", splay.rank(x));
else if (opt == 4) printf("%d\n", splay.kth(x));
else if (opt == 5) {
splay.insert(x); //把x先旋到根节点 而且一定要插入而不是直接旋 防止树上本来就没有x
printf("%d\n", splay.val[splay.findpre()]);
splay.del(x); //用完删掉
} else {
splay.insert(x); //同上
printf("%d\n", splay.val[splay.findnxt()]);
splay.del(x);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号