YBTOJ 6.1矩阵快速幂
A.序列的第k个数
要求熟练掌握等差数列和等比数列的第 \(k\) 项公式虽然你不熟练掌握随便推推也能推出来
然后写个快速幂就行了
code:
#include <bits/stdc++.h>
#define ll long long
#define int long long
using namespace std;
const int N = 10;
const ll mod = 200907;
int a[N], k, T;
ll ksm(int x, int i) {
ll res = 1;
while (i) {
if (i % 2 == 1) res = res * x % mod;
x = x * x % mod;
i = i >> 1;
}
return res;
}
signed main() {
scanf("%lld", &T);
while (T--) {
for (int i = 1; i <= 3; ++i) scanf("%lld", &a[i]);
scanf("%lld", &k);
if (a[1] + a[3] == a[2] << 1) {
printf("%lld\n", (a[1] + 1ll * (k - 1) * (a[2] - a[1]) % mod) % mod);
} else {
printf("%lld\n", a[1] * ksm(a[2] / a[1], (k - 1)) % mod);
}
}
return 0;
}
B.斐波那契数列
经典矩阵加速
首先递推地计算斐波那契复杂度是 \(O(n)\) 的
这里介绍一下矩阵加速
对于斐波那契的递推 显然有 \(f[i - 2] + f[i - 1] = f[i]\)
我们再考虑造一个形如 \(x * f[i - 2] + y * f[i - 1]\) 的柿子
发现 \(0 * f[i - 2] + 1 * f[i - 1] = f[i - 1]\)
进一步的 我们发现
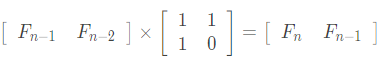
依次往下递推 就会得到 \(f_n\) 是
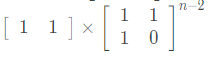
的第一项
code:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n;
const ll mod = 1e9 + 7;
struct node {
ll a[3][3];
};
void init(node &x) {
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= 2; ++j) x.a[i][j] = (i == j)? 1ll: 0ll;
}
}
void ch(node &x, node &y, node &z) {
memset(z.a, 0, sizeof(z.a) );
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= 2; ++j) {
for (int r = 1; r <= 2; ++r) {
z.a[i][j] += x.a[i][r] * y.a[r][j];
z.a[i][j] %= mod;
}
}
}
}
node ksm(node &x, ll k) {
node res;
init(res);
node ans;
node tmp = x;
while(k) {
if (k & 1) ch(res, tmp, ans), res = ans;
ch(tmp, tmp, ans), tmp = ans;
k >>= 1;
}
return res;
}
int main() {
scanf("%lld", &n);
node x;
x.a[1][1] = 1ll, x.a[1][2] = 1ll, x.a[2][1] = 1ll, x.a[2][2] = 0ll;
if (n == 1 || n == 2) {
printf("1");
return 0;
}
node ans = ksm(x, n - 2);
printf("%lld", (ans.a[1][1] + ans.a[1][2]) % mod);
return 0;
}
C.行为方案
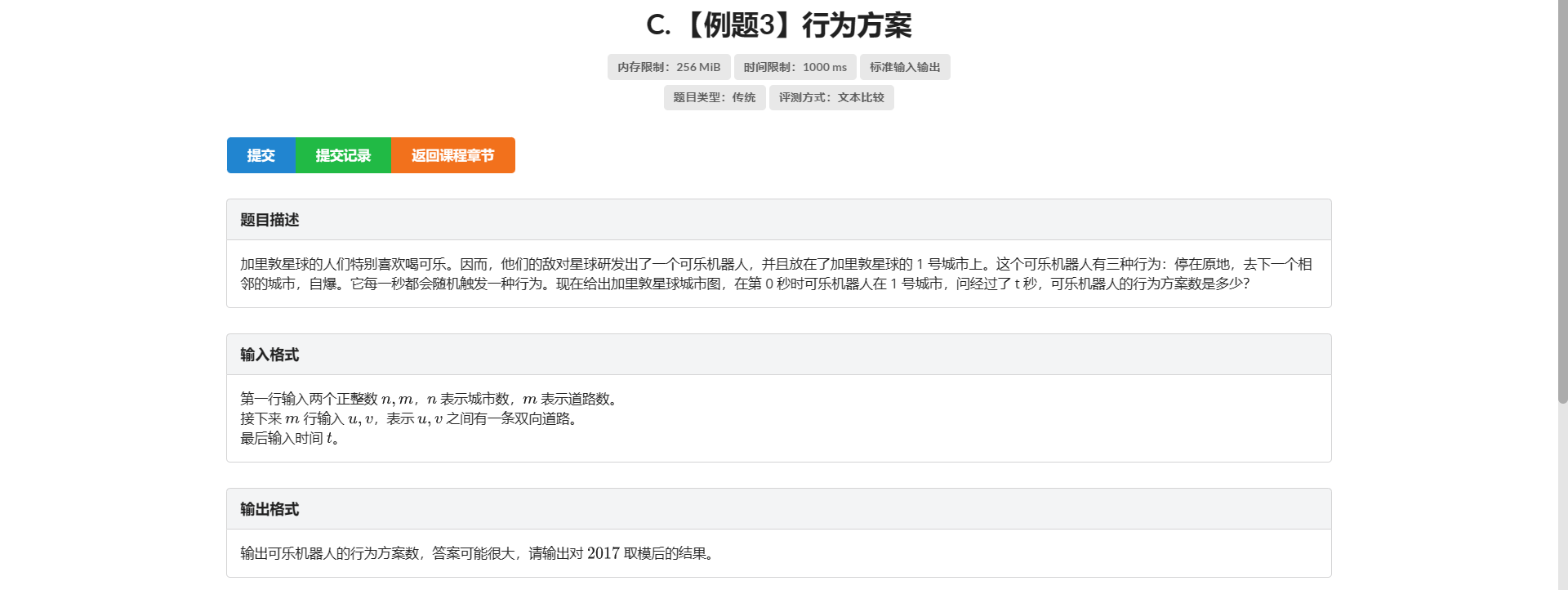
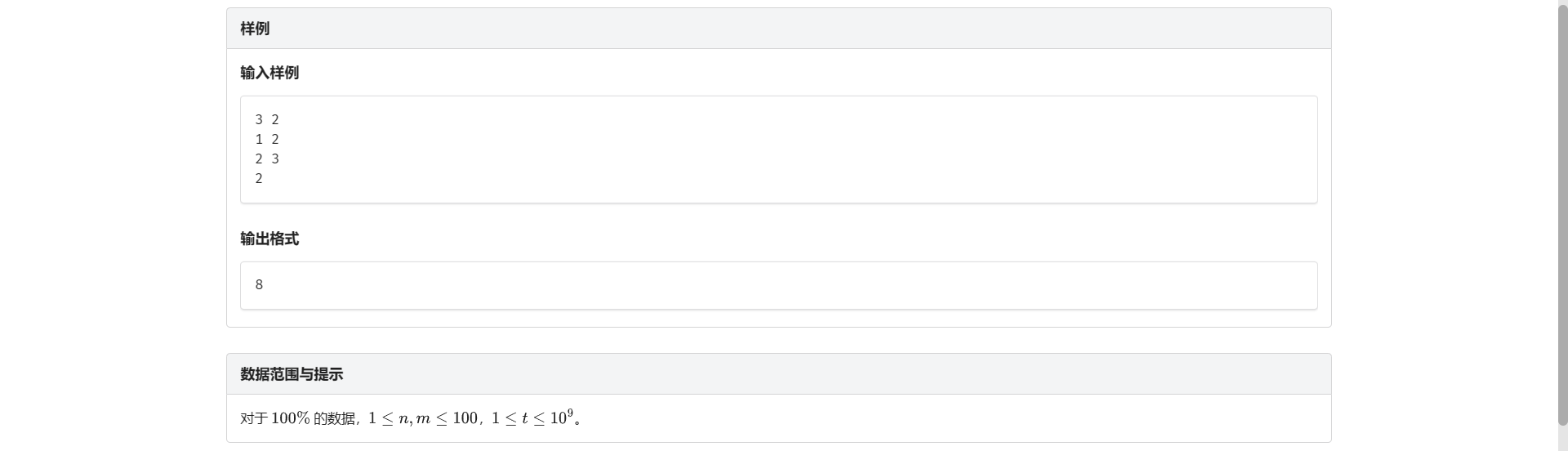
顶针 DP 麻了 真麻了
首先操作很多 我们考虑同化
停留原地视为走自环 自爆视为走到 0 点不回来
考虑转移
设 \(f_{i, j, k}\) 表示从 \(i\) 走到 \(j\) 一共走了 \(k\) 步的方案数
那显然有 \(f_{x, z, i + j} = \sum {(f_{x, y, i} \times f_{y, z, j})}\)
这个东西可以用矩快优化 具体可以参考YBTOJ 6.1例5 最短路径 题解
#include <bits/stdc++.h>
using namespace std;
const int N = 101;
const int mod = 2017;
struct node {
int a[N][N];
} mp;
int n, m, t;
void init(node &x) {
for (int i = 0; i <= n; ++i) x.a[i][i] = 1;
}
void ch(node &x, node &y, node &z) {
memset(z.a, 0, sizeof(z.a));
for (int i = 0; i <= n; ++i) {
for (int j = 0; j <= n; ++j) {
for (int loc = 0; loc <= n; ++loc) {
z.a[i][j] += x.a[i][loc] * y.a[loc][j];
z.a[i][j] %= mod;
}
}
}
}
node ksm(node &x, int k) {
node res;
init(res);
node tmp = x, ans;
while(k) {
if (k & 1) ch(res, tmp, ans), res = ans;
ch(tmp, tmp, ans), tmp = ans;
k >>= 1;
}
return res;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
mp.a[x][y] = mp.a[y][x] = 1;
}
scanf("%d", &t);
for (int i = 1; i <= n; ++i) mp.a[i][i] = mp.a[i][0] = 1;
mp.a[0][0] = 1;
node ret = ksm(mp, t);
int ans = 0;
for (int i = 0; i <= n; ++i) {
ans += ret.a[1][i];
ans %= mod;
}
printf("%d",ans);
return 0;
}
D.矩阵求和
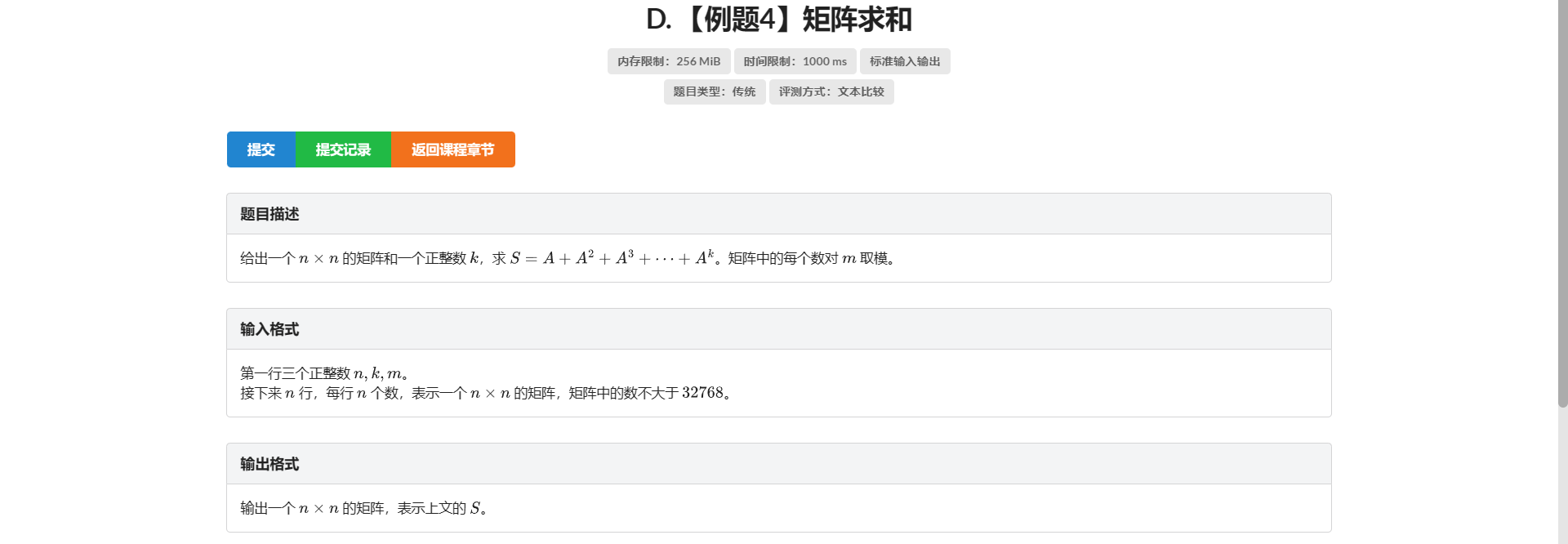
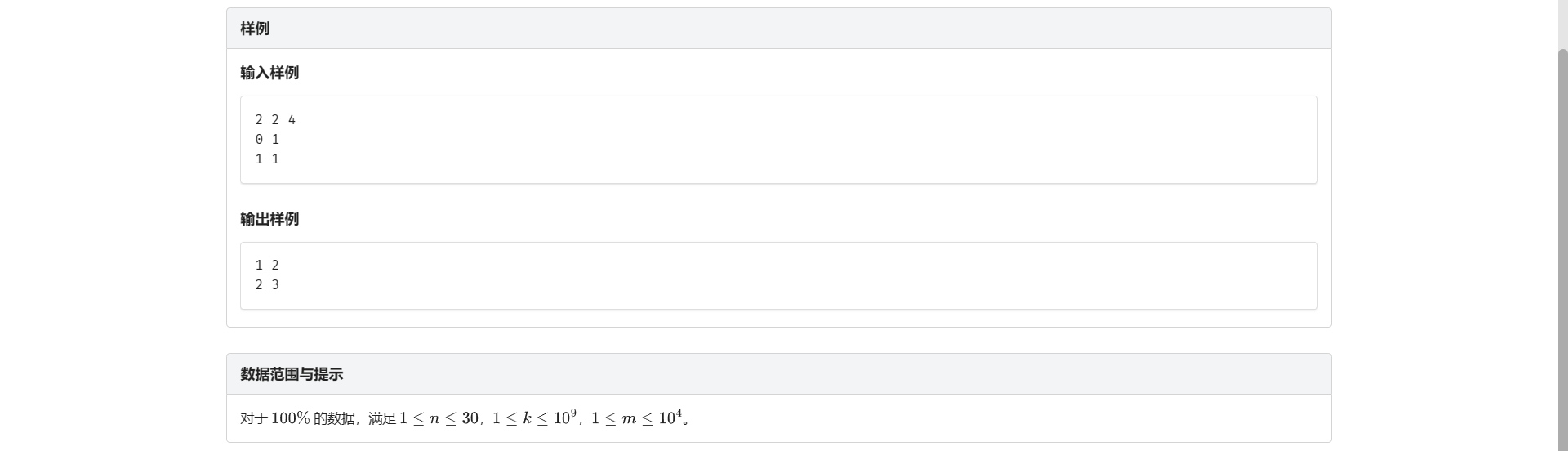
暴力怎么写很显然
暴力过不去也很显然
这题的关键在于矩阵套矩阵 那么我们构造一个矩阵 使ta的某一个元素为 \(\sum\limits_{i=1}^kA^i\) 即可
那么我们思考一下怎么构造
首先在此矩阵里构造一个 A 的 x + 1 次项是非常简单的
然后这个时候假如我们的矩阵里还有 \(\sum\limits_{i=1}^xA^i\) 那我们就能转移出下一个矩阵的对应
并且在下一项中应该还有 A 的 x + 2 次项在对应位置
那么我们可以猜这个项是由 A 的 x + 1 次项乘 A 加上一个什么项乘 0 得到的
同理 sum 项由原来的 sum 项乘 I 加上 A 的 x + 1 次项得到的
然后经过一顿蒙数学直觉的猜想 就可以构造出下面这个矩阵:
\(\begin{vmatrix}A&I\\0&I\end{vmatrix}\)
ta正好满足上述的所有性质
答案即为这个矩阵的 k + 1 次方的右上角元素减一个单位矩阵
#include <bits/stdc++.h>
using namespace std;
const int N = 31;
int n, m, k;
struct Matrix {
int a[N][N];
};
struct node {
Matrix a[3][3];
};
void init_Matrix(Matrix &x) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i == j) x.a[i][j] = 1;
else x.a[i][j] = 0;
}
}
}
void set_Matrix(Matrix &x) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) x.a[i][j] = 0;
}
}
Matrix operator * (Matrix x, Matrix y) {
Matrix ret;
set_Matrix(ret);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
for (int k = 1; k <= n; ++k) {
ret.a[i][j] += x.a[i][k] * y.a[k][j];
ret.a[i][j] %= m;
}
}
}
return ret;
}
Matrix operator + (Matrix x, Matrix y) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
x.a[i][j] = x.a[i][j] + y.a[i][j];
x.a[i][j] %= m;
}
}
return x;
}
void init_node(node &x) {
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= 2; ++j) {
if (i == j) init_Matrix(x.a[i][j]);
else set_Matrix(x.a[i][j]);
}
}
}
void set_node(node &x) {
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= 2; ++j) set_Matrix(x.a[i][j]);
}
}
node operator * (node x, node y) {
node ret;
set_node(ret);
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= 2; ++j) {
for (int k = 1; k <= 2; ++k) {
Matrix tmp = x.a[i][k] * y.a[k][j];
ret.a[i][j] = ret.a[i][j] + tmp;
}
}
}
return ret;
}
void print(node x) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i == j) printf("%d ",(x.a[1][2].a[i][j] - 1 + m) % m);
else printf("%d ",x.a[1][2].a[i][j]);
}
printf("\n");
}
}
node ksm_node(node x, int k) {
node ret;
init_node(ret);
while (k) {
if (k & 1) ret = ret * x;
x = x * x;
k >>= 1;
}
return ret;
}
int main() {
scanf("%d%d%d", &n, &k, &m);
node x;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) scanf("%d", &x.a[1][1].a[i][j]);
}
init_Matrix(x.a[1][2]);
init_Matrix(x.a[2][2]);
set_Matrix(x.a[2][1]);
x = ksm_node(x, k + 1);
print(x);
return 0;
}
(关于print函数里那个+m ybt上不加m才能AC 但是实际上你不加m连样例都过不去 std出大锅)
E.最短路径
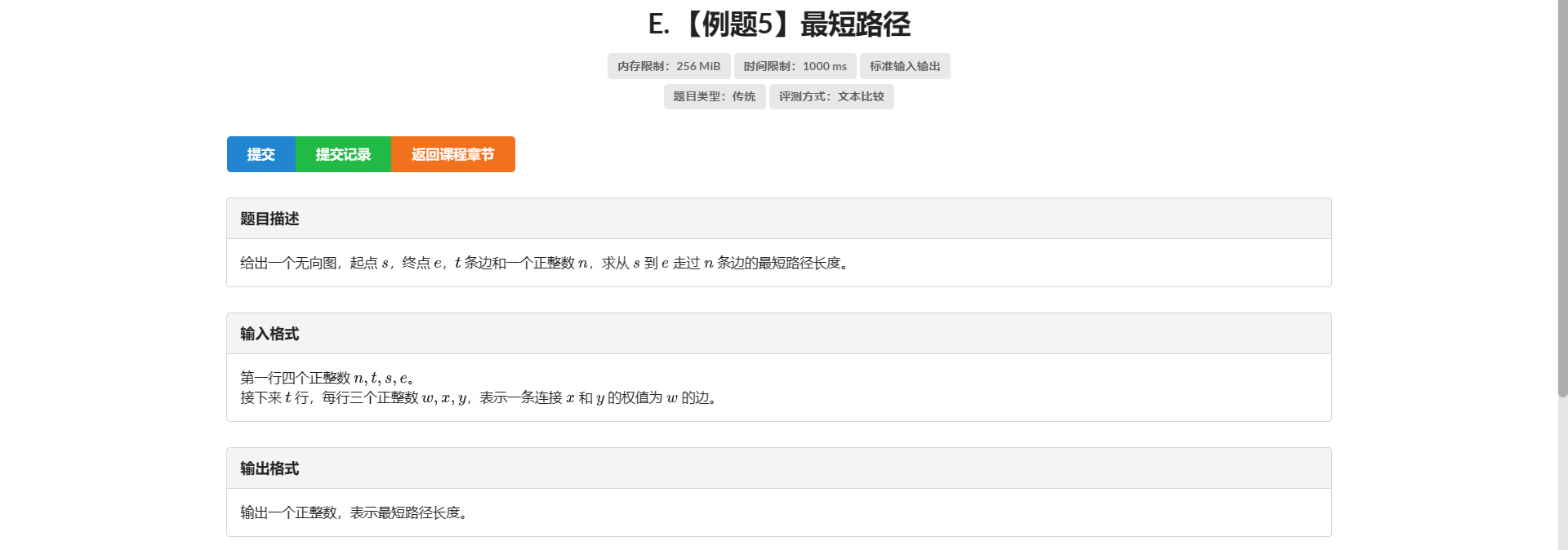
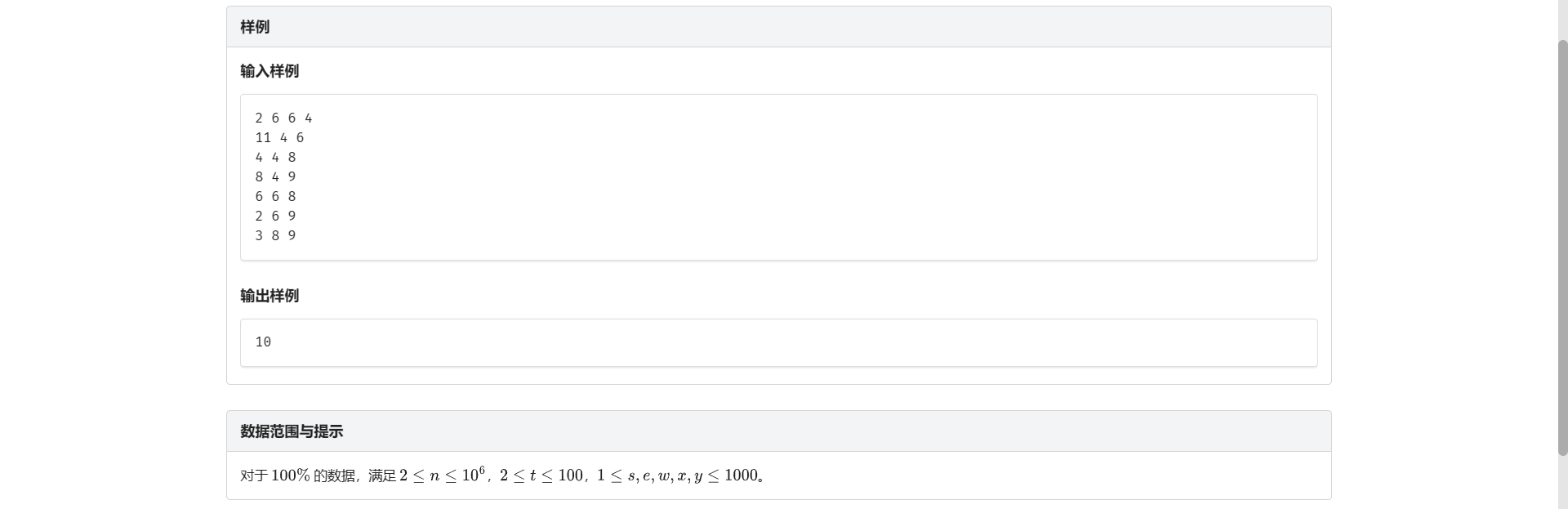
同样 考虑 \(f_{i, j, k}\) 表示从 \(i\) 到 \(j\) 走了 \(k\) 条边的最短路长度
那么还是有 \(f_{x, z, i + j} = \min{(f_{x, y, i} + f_{y, z, j})}\)
同样矩快优化顶针 DP 就好了
#include <bits/stdc++.h>
using namespace std;
const int N = 250;
const int M = 0x0d00;
int n, t, s, e;
int cnt;
int id[M];
struct matrix {
int a[N][N];
};
matrix dp(matrix x, matrix y) {
matrix ret;
memset(ret.a, 0x3f, sizeof(ret.a) );
for (int i = 1; i <= cnt; ++i) {
for (int j = 1; j <= cnt; ++j) {
for (int k = 1; k <= cnt; ++k) ret.a[i][j] = min(ret.a[i][j], x.a[i][k] + y.a[k][j]);
}
}
return ret;
}
matrix ksm(matrix x, int k) {
matrix ret;
memset(ret.a, 0x3f, sizeof(ret.a) );
for (int i = 1; i <= cnt; ++i) ret.a[i][i] = 0;
while (k) {
if (k & 1) ret = dp(ret, x);
x = dp(x, x);
k >>= 1;
}
return ret;
}
int main() {
matrix ans;
memset(ans.a, 0x3f, sizeof(ans.a) );
scanf("%d%d%d%d", &n, &t, &s, &e);
for (int i = 1; i <= t; ++i) {
int x, y, z;
scanf("%d%d%d", &z, &x, &y);
if (id[x] == 0) id[x] = ++cnt;
if (id[y] == 0) id[y] = ++cnt;
ans.a[id[x]][id[y]] = z;
ans.a[id[y]][id[x]] = z;
}
ans = ksm(ans, n);
printf("%d",ans.a[id[s]][id[e]]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号