YBTOJ 5.6单调队列
A.滑动窗口
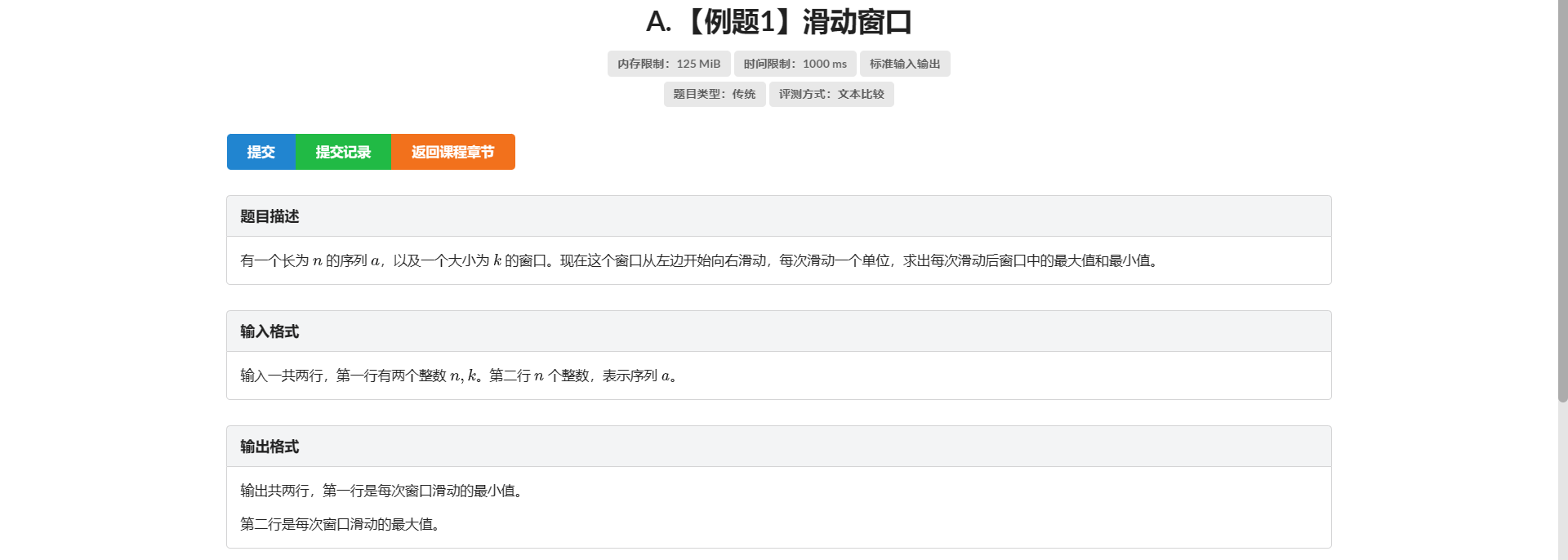
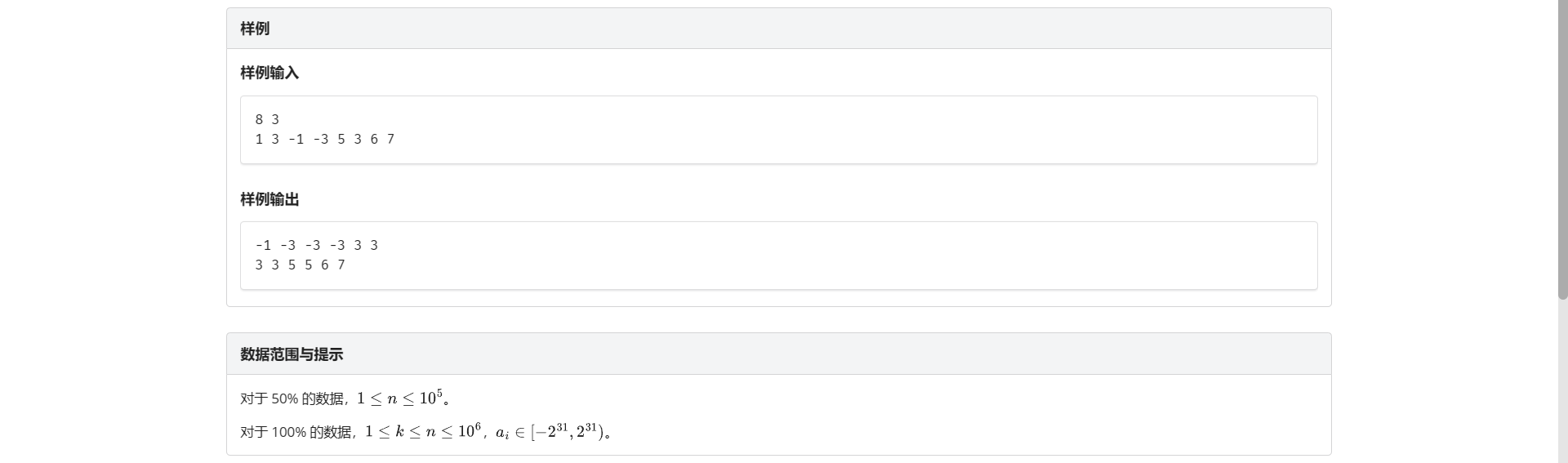
板子题
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1000037;
long long a[N];
int qmax[N], qmin[N];
int main() {
int n, k;
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
int hmin = 0, tmin = -1;
for (int i = 1; i <= n; i++) {
if (hmin <= tmin && i - qmin[hmin] >= k)
hmin++;
while (hmin <= tmin && a[i] < a[qmin[tmin]]) tmin--;
qmin[++tmin] = i;
if (i >= k)
printf("%lld ", a[qmin[hmin]]);
}
printf("\n");
int hmax = 0, tmax = -1;
for (int i = 1; i <= n; i++) {
if (hmax <= tmax && i - qmax[hmax] >= k)
hmax++;
while (hmax <= tmax && a[i] > a[qmax[tmax]]) tmax--;
qmax[++tmax] = i;
if (i >= k)
printf("%lld ", a[qmax[hmax]]);
}
return 0;
}
B.粉刷木板
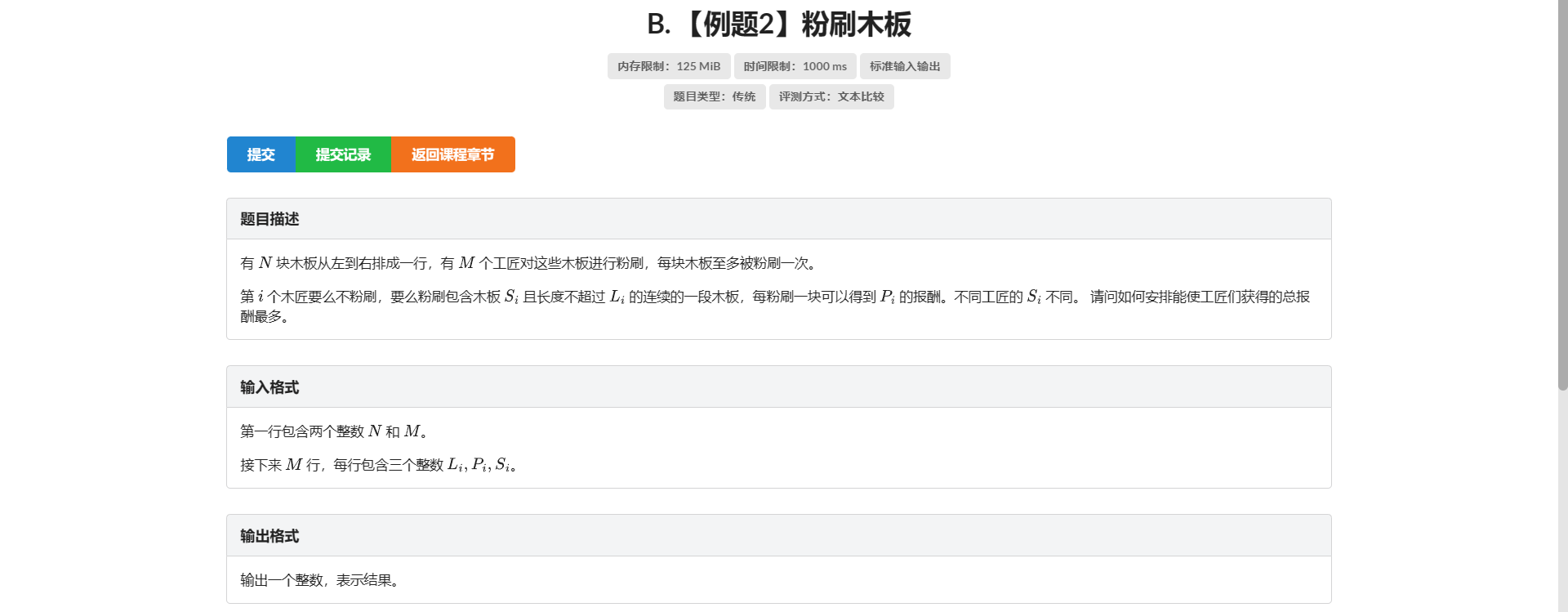
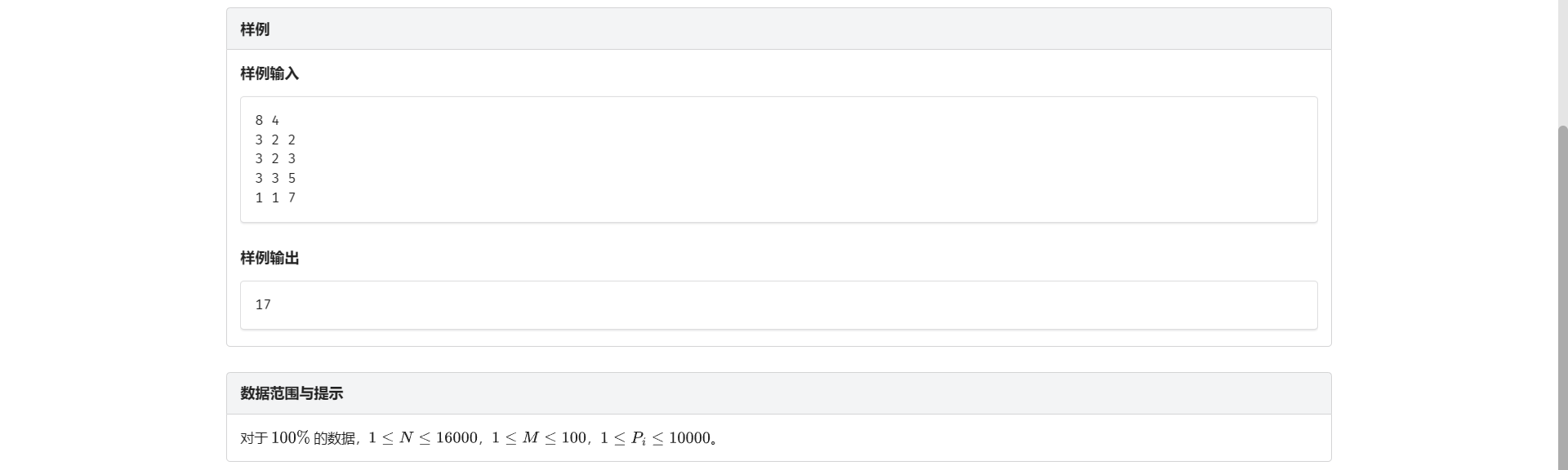
非常令人头疼的一道题
特别推荐下神 wind_whisper 的写法 不仅压到一维个人认为反而还比二维更为清晰明了
我们考虑每次刷对于整个序列的影响
因为要求的是一段连续长度不小于 \(L\) 的区间 所以我们考虑分别枚举左右端点
这样就有 \(f[r] = max(f[l] + (r - l) * p)\)
并且刷完之后要对后面点也进行更新 即 \(f[i] = max(f[i], f[i - 1])\)
这里我们就能发现一个转移顺序的问题 假如说你先转移了比较靠后的一段 然后转移了另一个比较靠前并且价值很大的一段 那么更新的时候就会把比较靠后的一段的贡献刷掉
所以要对 \(s\) 进行排序然后再转移
但是发现这样的做法是 \(O(m * n^2)\) 的 考虑优化
显然问题出在对 \(l\) \(r\) 的枚举上 我们想想能否优化这个过程
那我们考虑这题里的 \(l\) \(r\) 有什么特殊之处 然后我们就发现了 \(l\) \(r\) 之差不小于 \(L\)
进一步考虑 也就是说 对于一个给定的 \(l\) 它的 \(r\) 一定是在一段长度固定的区间里
又因为这题要求最大值 所以考虑能否用单调队列优化
但是又因为这题要转移的是 \(f[r]\) 所以我们应该是固定 \(r\) 然后把 \(l\) 用单调队列优化掉
那我们把 \(r\) 提出来 就有 \(f[r] = r * p + max(f[l] - p * l)\) 后面那坨就可以用单调队列优化
代码我写的二维的 比较臃肿
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e4 + 0721;
const int M = 121;
int f[M][N];
int q[N], h, t;
struct node {
int l, p, s;
friend bool operator<(node a, node b) {
return a.s < b.s;
}
} ban[M];
int n, m;
signed main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) scanf("%d%d%d", &ban[i].l, &ban[i].p, &ban[i].s);
sort(ban + 1, ban + 1 + m);
for (int i = 1; i <= m; ++i) {
h = 1, t = 0;
for (int k = max(0, (ban[i].s - ban[i].l)); k < ban[i].s; ++k) {
while (h <= t && f[i - 1][q[t]] - q[t] * ban[i].p <= f[i - 1][k] - k * ban[i].p) --t;
q[++t] = k;
}
for (int j = 1; j <= n; ++j) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (j >= ban[i].s) {
while (h <= t && j - q[h] > ban[i].l) ++h;
if (h <= t) f[i][j] = max(f[i][j], (j - q[h]) * ban[i].p + f[i - 1][q[h]]);
}
}
}
printf("%d",f[m][n]);
return 0;
}
C.耗费体力
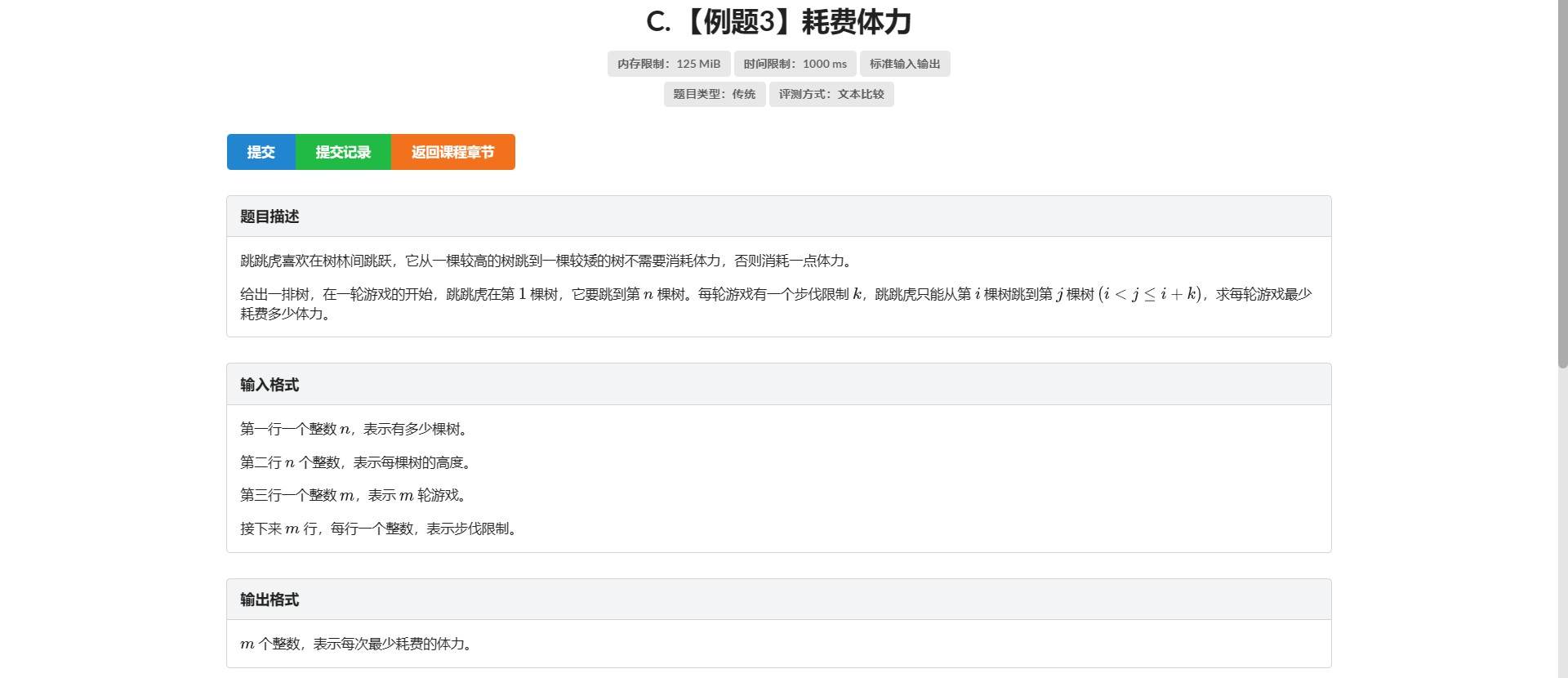
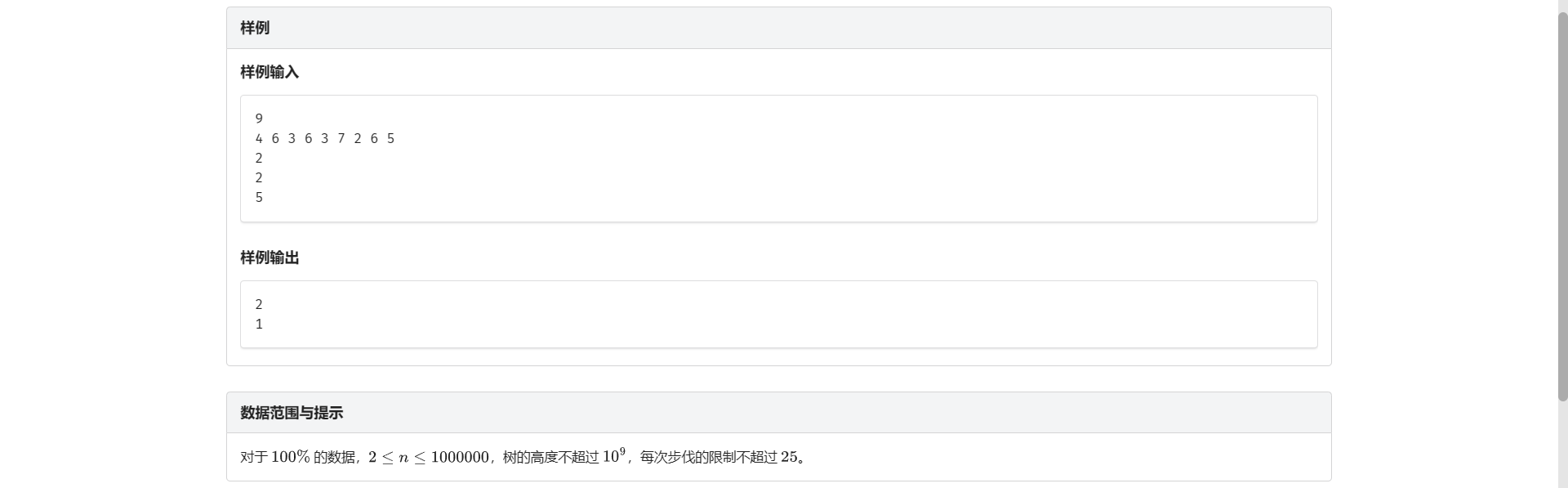
生动形象地诠释了题干的每个条件都不白给
设 \(f[i]\) 表示跳到 \(i\) 的最小体力花费
容易有
- \(f[i] = f[k] (h[k] > h[i])\)
- \(f[i] = f[k] + 1 (h[k] \le h[i])\)
然后 \(k\) 显然是 \(i\) 前面一段长度固定的区间 可以单调队列优化
然后就卡住了
瓶颈在于因为 \(k\) 分高于 \(i\) 和低于 \(i\) 两种
我们考虑“比你小还比你强原则” 能想到优先让 \(f\) 值小的在里面 \(f\) 值相同就优先让高度大的在里面 因为更有可能触发 \(h[k] > h[i]\)
那么这么干很容易想到一个问题:有没有可能这个点 \(f\) 值小但是比较矮会触发额外体力耗费 然后它后面有个不会触发额外体力耗费的稍大一点的点 那就会出问题
然后发现题干中额外体力耗费固定是 \(1\)
所以以上那种情况不可能发生 撑死是等于 这样做一定不会更劣
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 0721;
int a[N], q[N], f[N];
int h, t;
int n, m;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
scanf("%d", &m);
while (m--) {
int len;
scanf("%d", &len);
h = 1, t = 0;
q[++t] = 1;
for (int i = 2; i <= n; ++i) {
while (h <= t && i - q[h] > len) ++h;
if (a[q[h]] > a[i]) f[i] = f[q[h]];
else f[i] = f[q[h]] + 1;
while (f[i] < f[q[t]] || (f[i] == f[q[t]] && a[i] >= a[q[t]])) --t;
q[++t] = i;
}
printf("%d\n",f[n]);
}
return 0;
}
D.燃放烟火
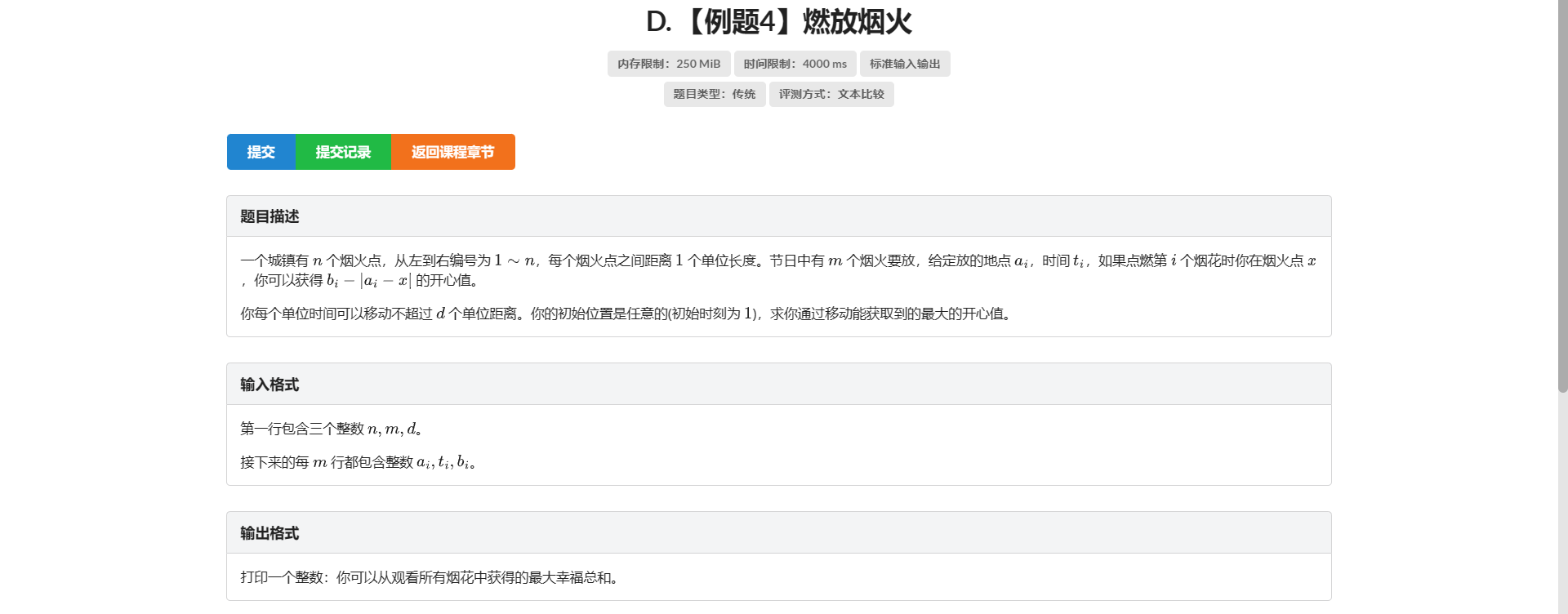
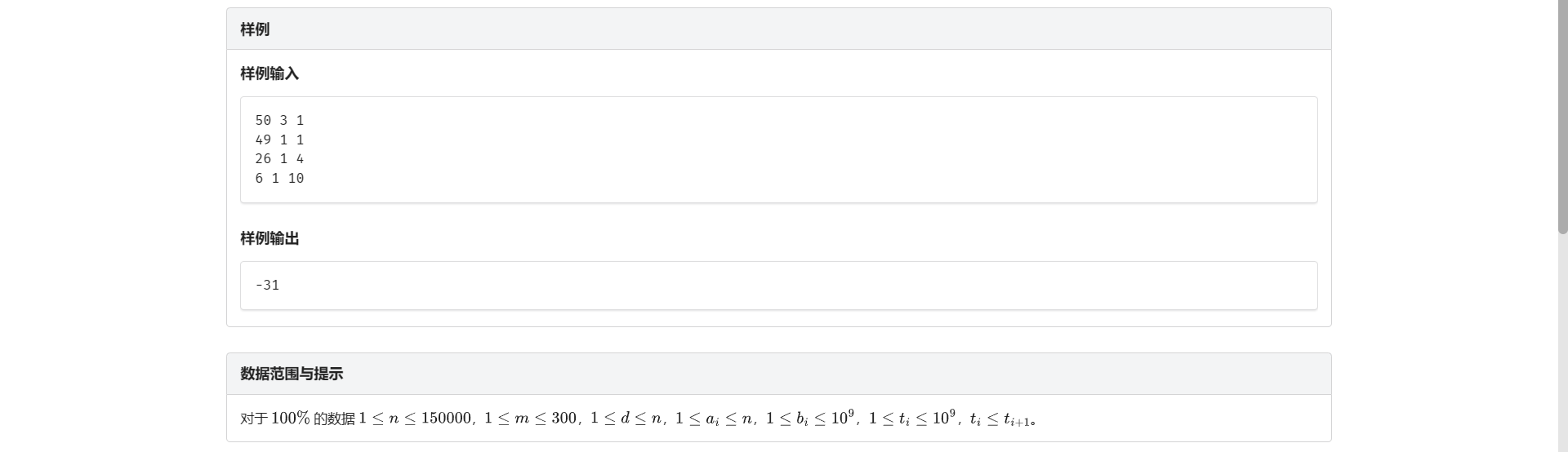
首先考虑简化条件 \(t_i\) 和 \(d\) 放一起显然就代表着两次烟火之间能移动的最大距离
我们设 \(f[i][j]\) 表示燃放第 \(i\) 个烟火时在 \(j\) 位置的最大幸福值
然后显然 \(f[i][j]\) 的状态能从 \(f[i - 1]\) 中 \(j\) 前面加后面一段连续的区间转移过来
这里要注意一个问题 因为单调队列优化 \(DP\) 只能更新当前定区间结尾的 \(DP\) 值
所以对于目标状态夹在中间的 我们要正反扫两遍
又因为 \(f[i]\) 只和 \(f[i - 1]\) 有关 所以开两个数组来回滚就行
复杂度 \(O(m * n)\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 152152;
ll f[2][N];
int t[N], q[N];
int n, m, d;
int main() {
scanf("%d%d%d", &n, &m, &d);
int p = 0;
for (int i = 1; i <= m; ++i) {
p = 1 - p;
int a, b;
scanf("%d%d%d", &a, &b, &t[i]);
ll len = 1ll * (t[i] - t[i - 1]) * d;
int h = 1, t = 0;
for (int j = 1; j <= n; ++j) {
while (h <= t && j - q[h] > len) ++h;
while (h <= t && f[1 - p][q[t]] < f[1 - p][j]) --t;
q[++t] = j;
f[p][j] = f[1 - p][q[h]] - abs(a - j) + b;
}
h = 1, t = 0;
for (int j = n; j >= 1; --j) {
while (h <= t && q[h] - j > len) ++h;
while (h <= t && f[1 - p][q[t]] < f[1 - p][j]) --t;
q[++t] = j;
f[p][j] = max(f[p][j], f[1 - p][q[h]] - abs(a - j) + b);
}
}
ll ans = -0x7ffffffffffffff;
for (int i = 1; i <= n; ++i) ans = max(ans, f[p][i]);
printf("%lld",ans);
return 0;
}
E.跳房子
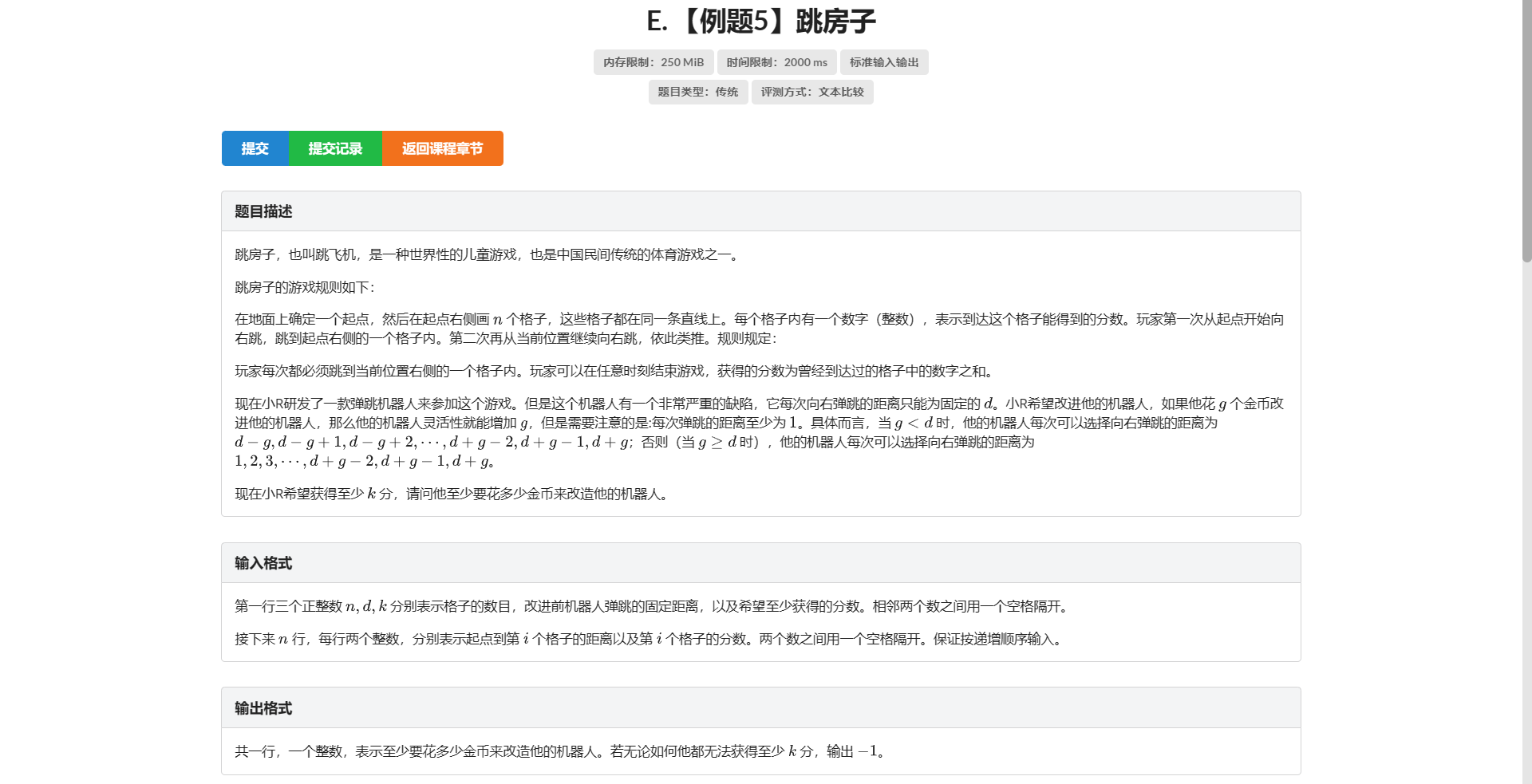
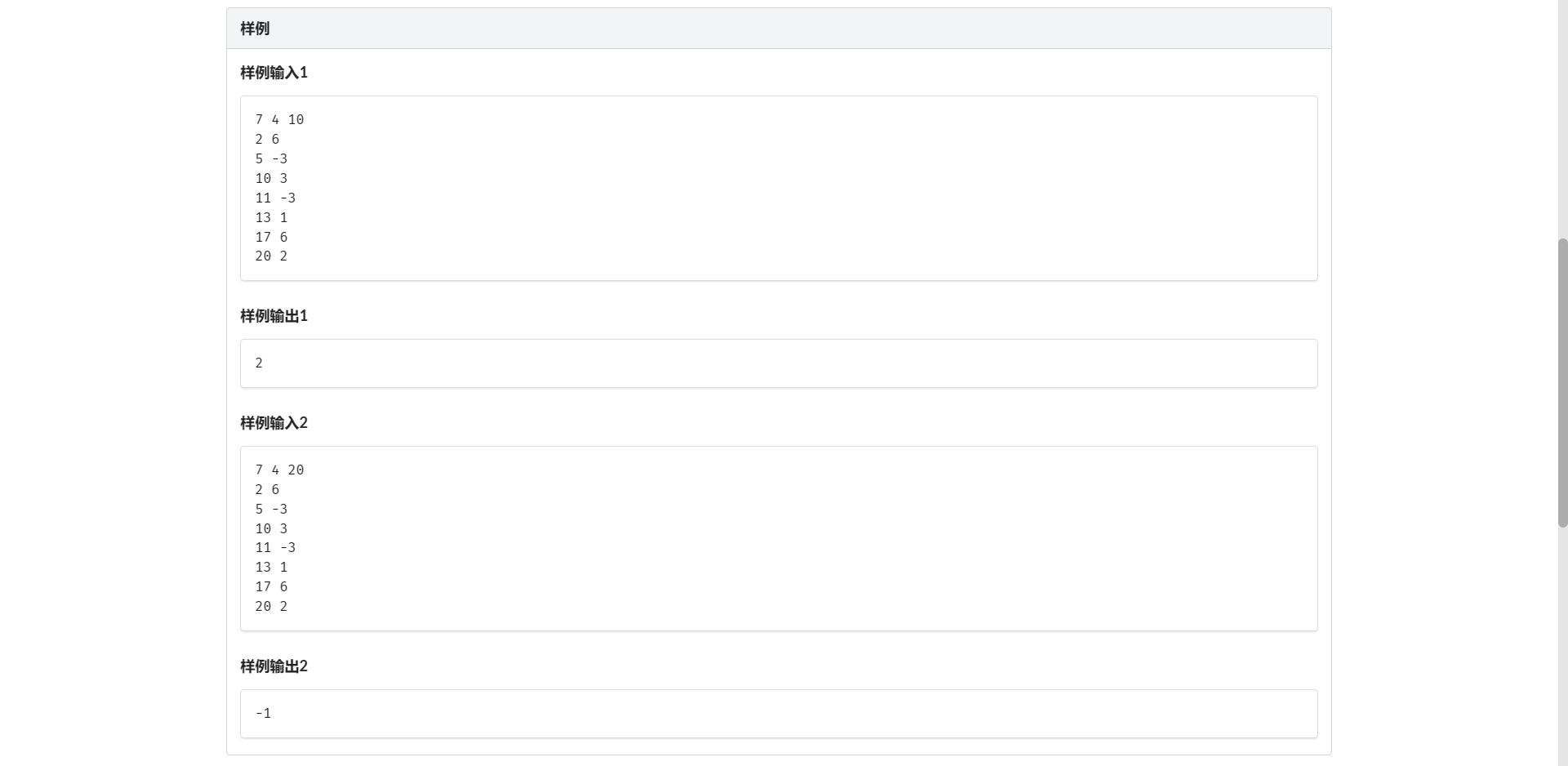

这竟然是道普及组的题
至少花多少金币 看起来就很二分
我们还是设 \(f[i]\) 表示跳到第 \(i\) 格的最大得分 考虑能从哪转移过来
发现是 \(i\) 前面和 \(i\) 隔着一些距离的连续一段定区间
那就上单调队列
那如何控制这个队列队尾元素的位置呢 实际上再弄个指针就行了
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e5 + 0721;
const ll inf = 0x7ffffffffffffff;
int loc[N], c[N], q[N];
ll f[N];
int n, d, k;
bool check(int x) {
int l = max(1, d - x), r = d + x;
f[0] = 0;
for (int i = 1; i <= n; ++i) f[i] = -inf;
int h = 1, t = 0, j = 0;
for (int i = 1; i <= n; ++i) {
while (loc[i] - loc[j] >= l) {
while (h <= t && f[q[t]] < f[j]) --t;
q[++t] = j;
++j;
}
while (h <= t && loc[i] - loc[q[h]] > r) ++h;
if (h <= t) f[i] = f[q[h]] + c[i];
if (f[i] >= k) return 1;
}
return 0;
}
int main() {
scanf("%d%d%d", &n, &d, &k);
for (int i = 1; i <= n; ++i) scanf("%d%d", &loc[i], &c[i]);
int l = 0, r = loc[n];
int ans, mid;
while (l <= r) {
mid = l + (r - l >> 1);
if (check(mid)) {
ans = mid;
r = mid - 1;
} else
l = mid + 1;
}
if (l >= loc[n]) printf("-1");
else printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号