YBTOJ 5.5状压DP
A.种植方案
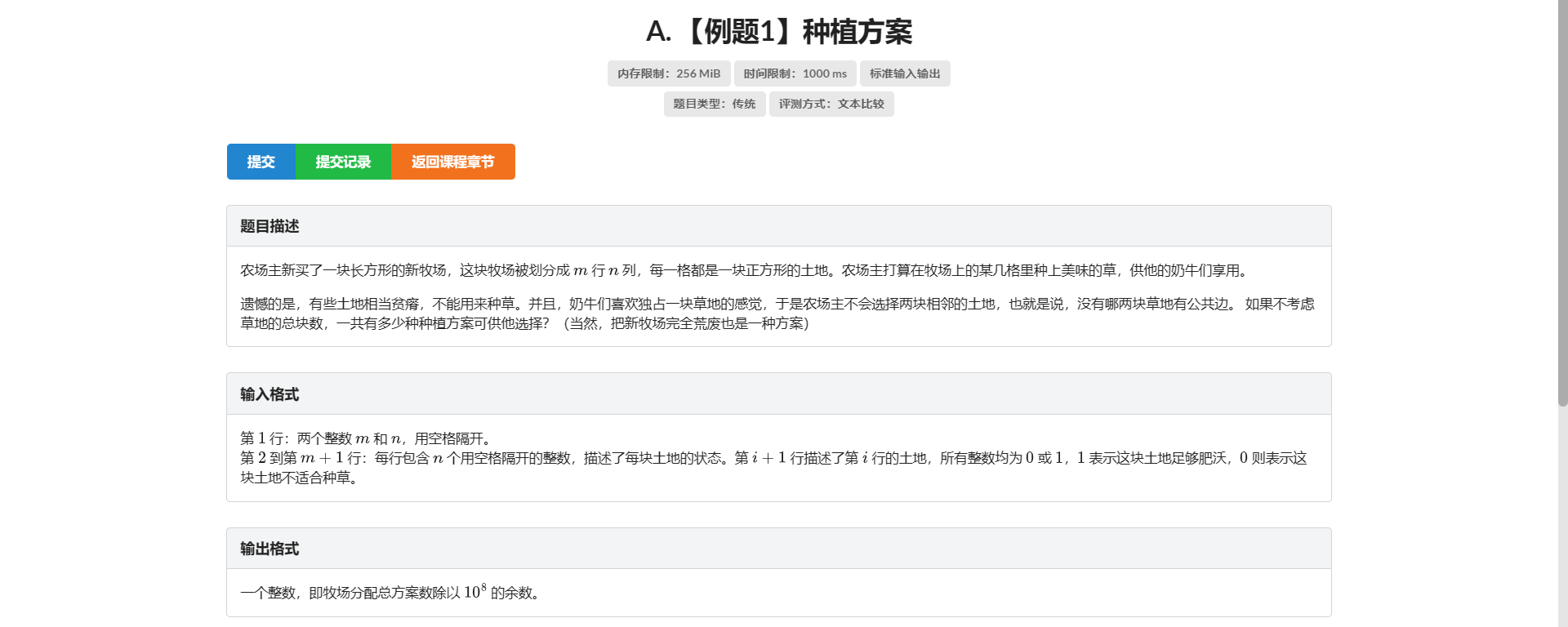
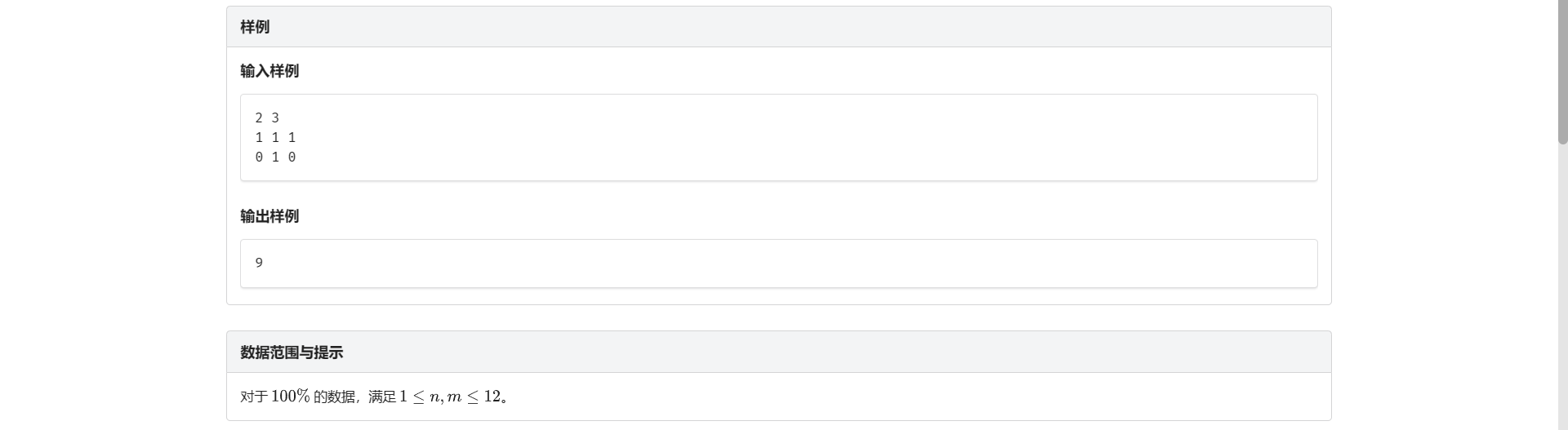
范围看起来很状压 放不放奶牛看起来也很状压 那我们就状压
首先判左右不同时有 那就判它左/右移一位和原来与起来为 \(0\)
然后判上下不同时有 那就判上一行和当前行与起来为 \(0\)
然后要判当前放置方案和地形是否符合 那就判它和地形与起来不为 \(0\)
有个常数上的小优化 就是提前枚举预处理出合法方案
但是不预处理直接暴力枚举也能过
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 0721;
const int M = 15;
const int mod = 1e8;
int loc[M];
int f[M][N];
int m, n;
int main() {
scanf("%d%d", &m, &n);
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
int x;
scanf("%d", &x);
loc[i] += ((1 - x) << j - 1);
}
// cout << i << " " << loc[i] << "\n";
}
for (int j = 0; j <= (1 << n) - 1; ++j) {
// cout << j << endl;
if (((j & loc[1]) == 0) && ((j & (j >> 1)) == 0) && ((j & (j << 1)) == 0)) {
// cout << j << endl;
f[1][j] = 1;
}
}
f[1][0] = 1;
for (int i = 2; i <= m; ++i) {
for (int j = 0; j <= (1 << n) - 1; ++j) {
if ((j & (j << 1)) || (j & (j >> 1)))
continue;
if ((j & loc[i]) == 0 || j == 0) {
// cout << j << endl;
for (int k = 0; k <= (1 << n) - 1; ++k) {
if ((j & k) == 0 && ((k & (k << 1)) == 0) && ((k & (k >> 1)) == 0))
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
int sum = 0;
for (int i = 0; i <= (1 << n) - 1; ++i) {
sum = (sum + f[m][i]) % mod;
}
printf("%d",sum);
return 0;
}
B.最短路径
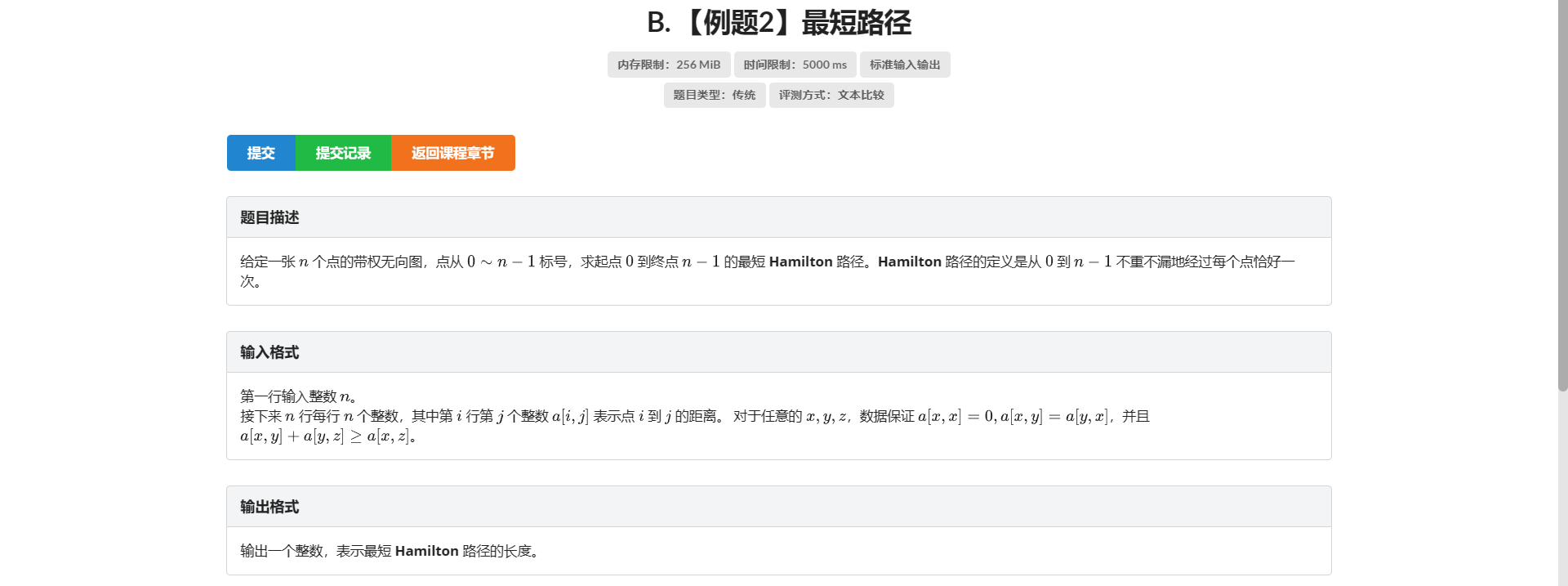
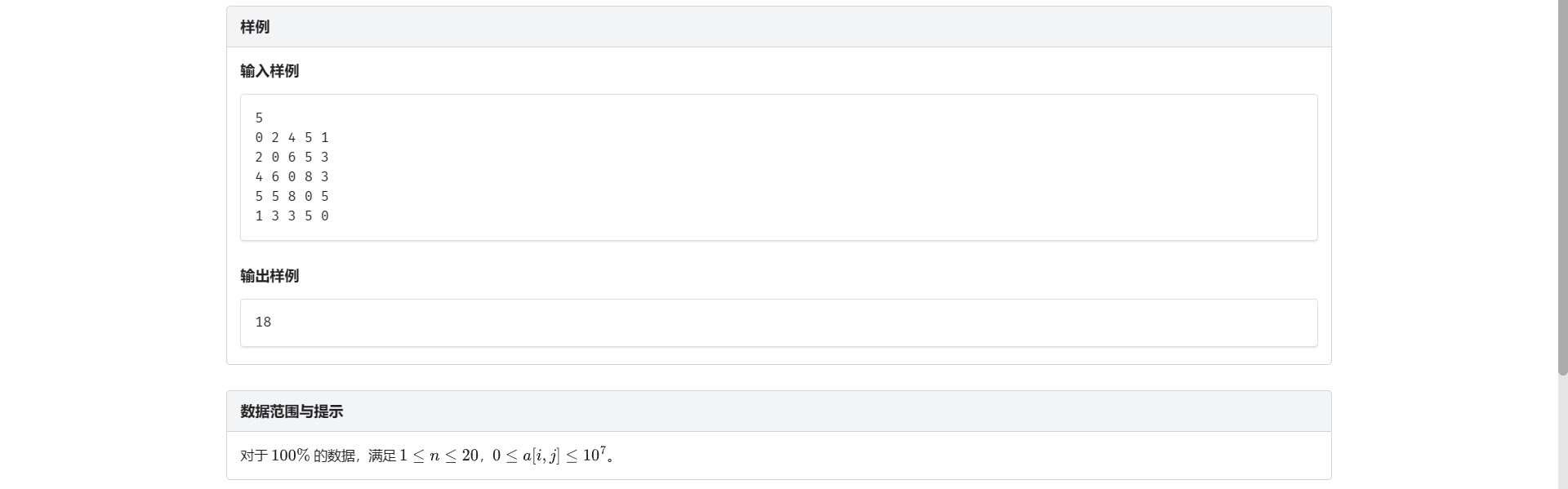
首先想到搜索 但是算一下也就只能过得去 \(n \le 10\) 的数据范围
那考虑一下这题与普通搜索题多了什么限制条件
发现如果是普通搜索 可以让每个点被经过多次
但是此题每个点只能被经过一次
所以说对于一个点来说 它只有两个状态:没被经过或者被经过一次
考虑状压 非常神奇的一个写法
设 \(f[i][j]\) 表示现在在第 \(i\) 个点 当前点的状态为 \(j\) 时的最短路
那我们枚举当前状态 \(j\) 作为外层循环 内层循环枚举当前的点 \(i\) 以及可以到达的点 \(k\)
然后判合法性 如果当前状态 \(j\) 中表示 \(i\) 或 \(k\) 的那位为 \(0\) 显然就不合法
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 22;
int dis[N][N], f[N][(1 << 21)];
int n;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) scanf("%d", &dis[i][j]);
}
memset(f, 0x3f, sizeof f );
f[1][1] = 0;
for (int j = 0; j < (1 << n); ++j) {
for (int i = 1; i <= n; ++i) {
if (!(j & (1 << i - 1))) continue;
for (int k = 1; k <= n; ++k) {
if (k == i) continue;
if (!(j & (1 << k - 1))) continue;
f[i][j] = min(f[i][j], f[k][j ^ (1 << i - 1)] + dis[i][k]);
}
}
}
printf("%d",f[n][(1 << n) - 1]);
return 0;
}
C.涂抹果酱
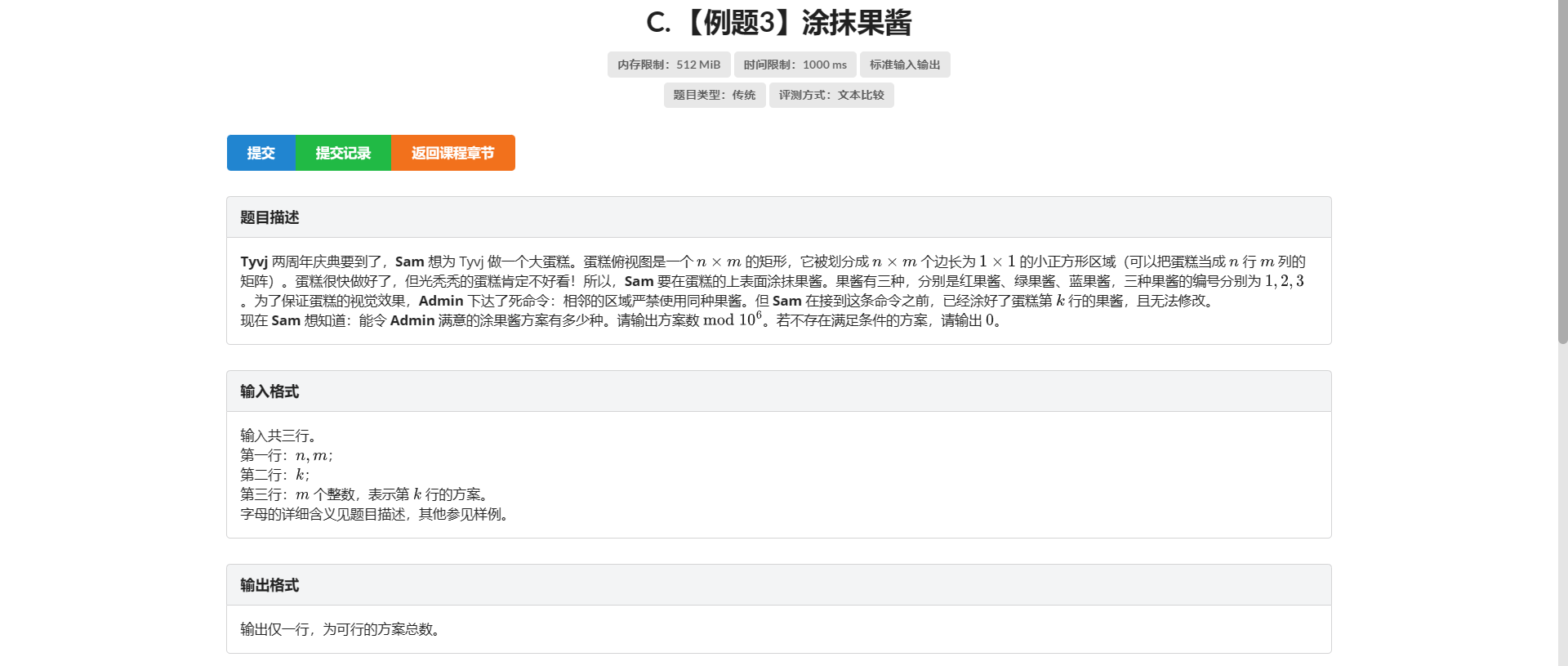
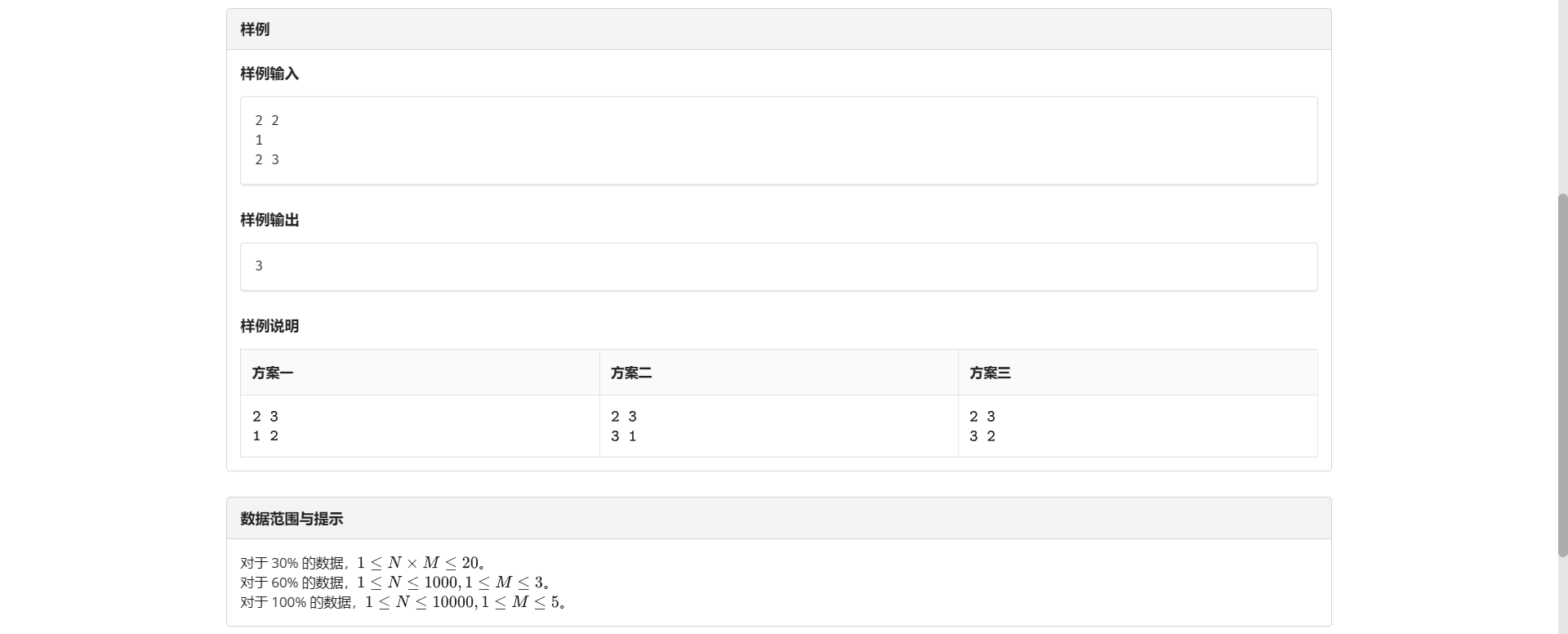
不难发现如果我们能写出三进制状压 这题就能秒
那我们研究一下三进制状压怎么写
首先位运算那一车东西肯定都要丢掉用不了
我们考虑将一个数化成三进制 显然是不断除 \(3\) 然后对 \(3\) 取模
那我们就可以记录范围内十进制数化成三进制的每一位
但是显然这个十进制很多 开数组空间不够用
进一步我们发现 我们只需要合法的三进制状态 即没有 \(0/1/2\) 左右相邻的状态
那我们就可以弄一个 \(tmp\) 数组把它拆掉然后判合法 合法之后再记录到要用的记录数组中
这样顺便也完成了离散化
这题同样可以预处理出合法状态来缩小常数
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
const int M = 10;
const int mod = 1e6;
bool valid[N][N];
int a[N][M], f[N][N];
int id[N];
int n, m, kk, sum, ans;
int tot;
void init_num() {
int t = pow(3, m);
for (int i = 0; i < t; ++i) {
int tmp[M], num = i, len = 0;
memset(tmp, 0, sizeof tmp );
while (num) {
tmp[++len] = num % 3;
num /= 3;
// cout << "1";
}
bool flag = 0;
for (int j = 2; j <= m; ++j) {
if (tmp[j] == tmp[j - 1]) {
flag = 1;
break;
}
}
if (!flag) {
id[i] = ++tot;
for (int j = 1; j <= m; ++j) a[tot][j] = tmp[j];
}
}
}
void init_valid() {
for (int i = 1; i <= tot; ++i) {
valid[i][i] = 0;
for (int j = i + 1; j <= tot; ++j) {
bool flag = 0;
for (int k = 1; k <= m; ++k) {
if (a[i][k] == a[j][k]) {
flag = 1;
break;
}
}
if (flag) valid[i][j] = valid[j][i] = 0;
else valid[i][j] = valid[j][i] = 1;
}
}
}
void dp() {
if (kk == 1) {
f[1][id[sum]] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= tot; ++j) {
for (int k = 1; k <= tot; ++k) {
if (valid[j][k]) f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
} else {
for (int i = 1; i <= tot; ++i) f[1][i] = 1;
for (int i = 2; i <= n; ++i) {
if (i == kk) {
for (int j = 1; j <= tot; ++j) {
if (valid[id[sum]][j]) f[i][id[sum]] = (f[i][id[sum]] + f[i - 1][j]) % mod;
}
} else {
for (int j = 1; j <= tot; ++j) {
for (int k = 1; k <= tot; ++k) {
if (valid[j][k]) f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
}
}
int main() {
scanf("%d%d", &n, &m);
scanf("%d", &kk);
for (int i = 0; i < m; ++i) {
int x;
scanf("%d", &x);
sum = sum * 3 + x - 1;
}
init_num();
init_valid();
dp();
for (int i = 1; i <= tot; ++i) ans = (ans + f[n][i]) % mod;
printf("%d",ans);
return 0;
}
D.炮兵阵地
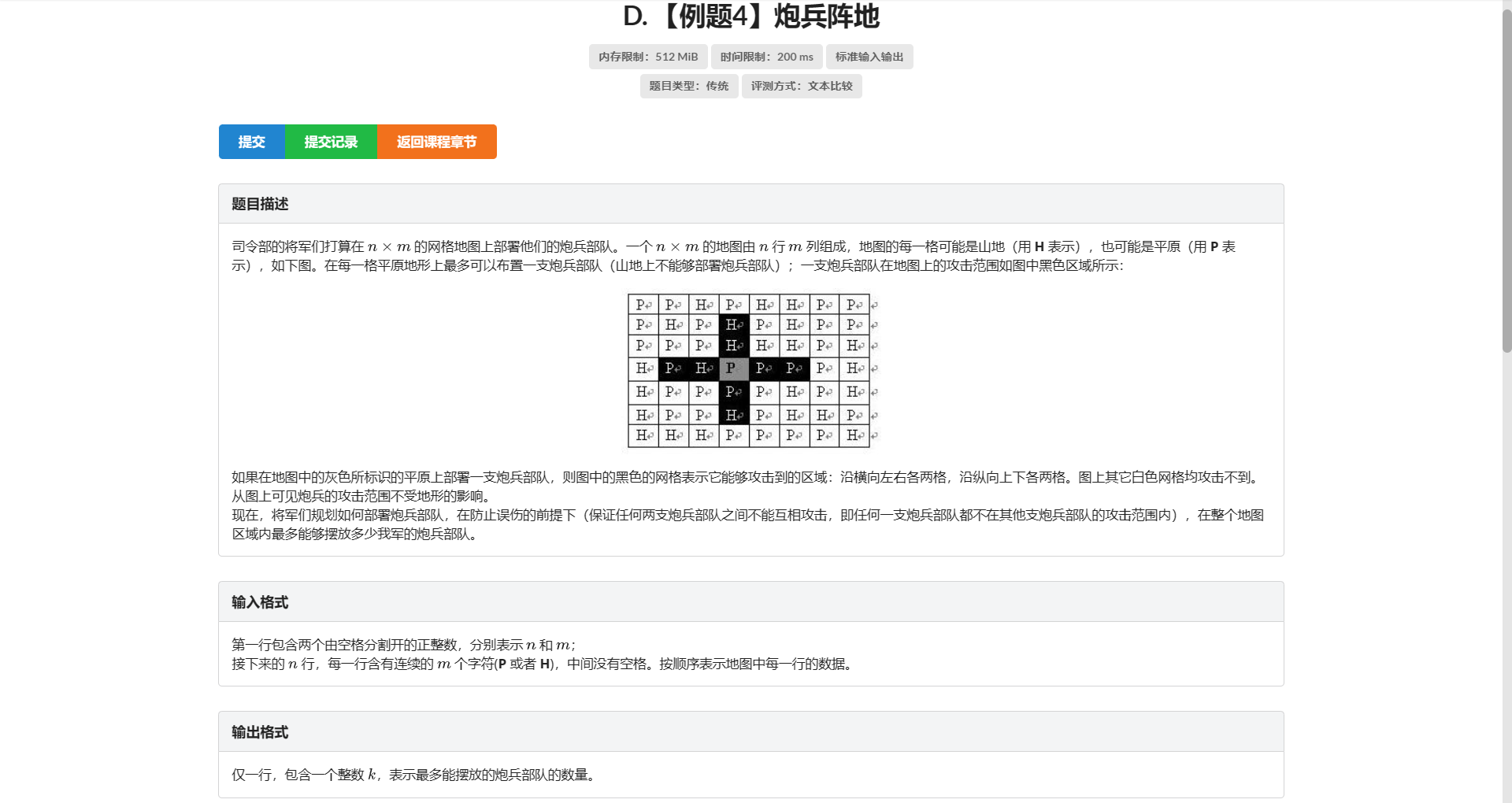
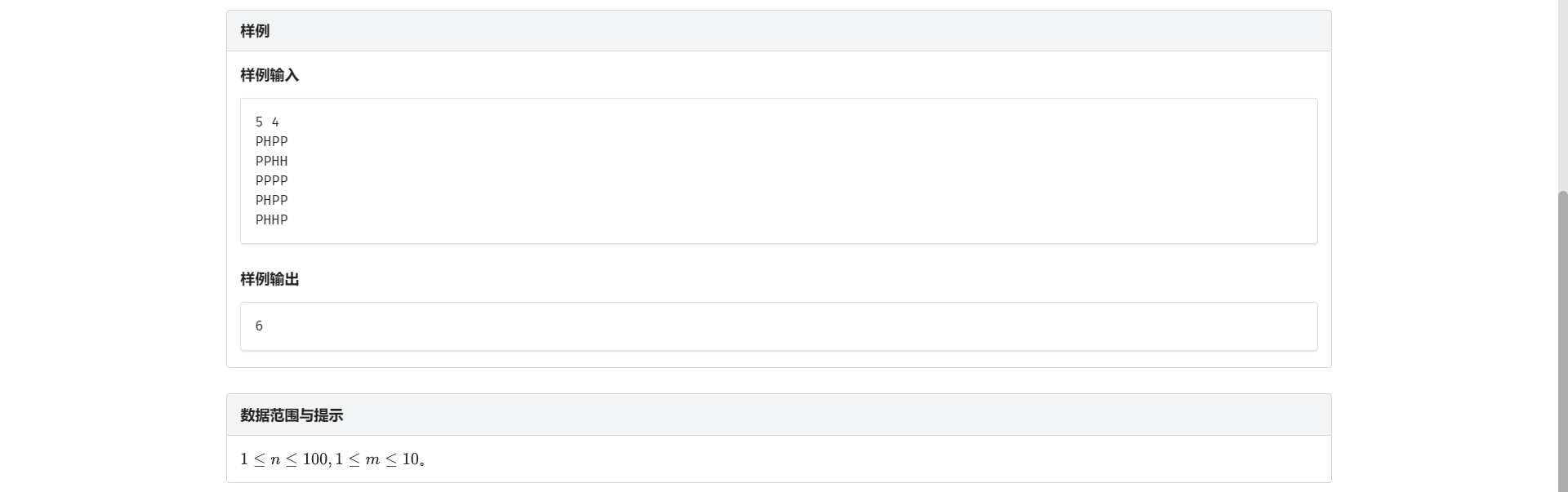
首先左和左左 右和右右是非常好判的 直接判左/右移 \(1/2\) 位即可
主要是如何判上和上上
首先我们还是看原来只用判上的 我们用 \(f[i][j]\) 表示第 \(i\) 行 当前状态为 \(j\) 的方案数
那么如果是上上 我们不妨扩展到 \(f[i][j][k]\) 表示第 \(i\) 行 当前状态为 \(j\) 上一行状态为 \(k\) 的方案数
转移式就比较显然了 主要是要预处理第 \(1\) \(2\) 行的方案数
(有一说一 越写越感觉到预处理对常数优化的强大作用)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
bool valid[N][N];
int f[N][N][N], val[N], s[N], mp[N], tot;
int n, m, ans;
inline int lowbit(int x) {
return x & (-x);
}
void init() {
for (int i = 0; i < (1 << m); ++i) {
if ((i & (i << 1)) || (i & (i << 2)) || (i & (i >> 1)) || (i & (i >> 2))) continue;
val[++tot] = i;
}
for (int i = 1; i <= tot; ++i) {
int tmp = val[i];
while (tmp) {
++s[i];
tmp -= lowbit(tmp);
}
}
for (int i = 1; i <= tot; ++i) {
valid[i][i] = 0;
for (int j = i + 1; j <= tot; ++j) {
if (val[i] & val[j]) valid[i][j] = valid[j][i] = 0;
else valid[i][j] = valid[j][i] = 1;
}
}
}
void dp() {
for (int i = 1; i <= tot; ++i) {
if (val[i] & mp[1]) continue;
for (int j = 1; j <= tot; ++j) {
if (val[j] & mp[2]) continue;
if (valid[i][j]) f[2][j][i] = s[i] + s[j];
}
}
for (int i = 3; i <= n; ++i) {
for (int j = 1; j <= tot; ++j) {
if (val[j] & mp[i]) continue;
for (int k = 1; k <= tot; ++k) {
if (!valid[j][k]) continue;
for (int l = 1; l <= tot; ++l) {
if (!valid[j][l]) continue;
if (!valid[k][l]) continue;
f[i][j][k] = max(f[i][j][k], f[i - 1][k][l] + s[j]);
}
}
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
char c;
cin >> c;
mp[i] <<= 1;
if (c == 'H') ++mp[i];
}
}
init();
dp();
for (int i = 1; i <= tot; ++i) {
for (int j = 1; j <= tot; ++j) ans = max(ans, f[n][i][j]);
}
printf("%d",ans);
return 0;
}
E.最优组队
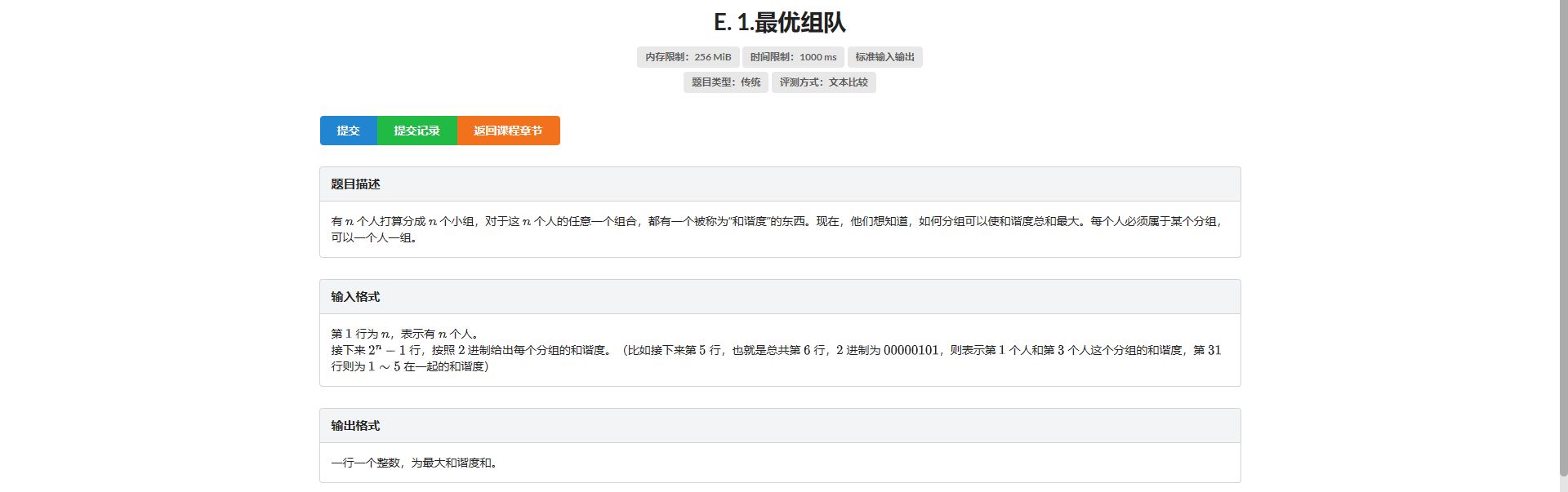
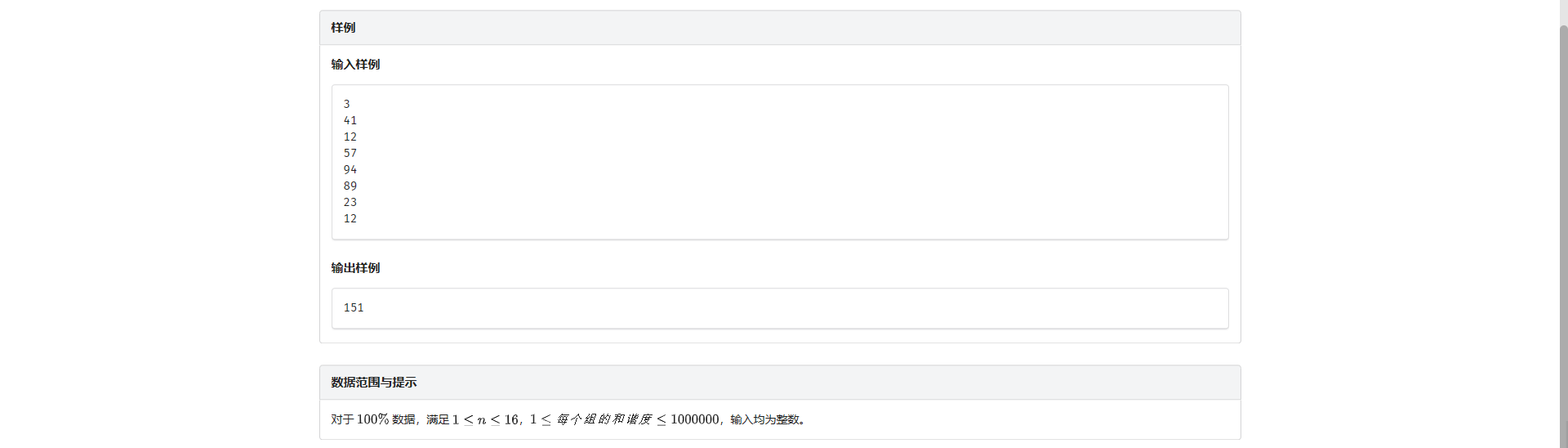
枚举子集 复杂度 \(\text{O}(3^n)\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
if (x < 0) putchar('-'), x = -x;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
const int N = 1e6 + 0721;
int f[N];
int n;
void main() {
n = read();
for (int i = 1; i <= (1 << n) - 1; ++i) f[i] = read();
for (int i = 1; i <= (1 << n) - 1; ++i) {
for (int j = i; j; j = (j - 1) & i) f[i] = max(f[i], f[i ^ j] + f[j]);
}
write(f[(1 << n) - 1]), putchar('\n');
}
}
int main() {
steven24::main();
return 0;
}
/*
3
41
12
57
94
89
23
12
*/
F.最短路径
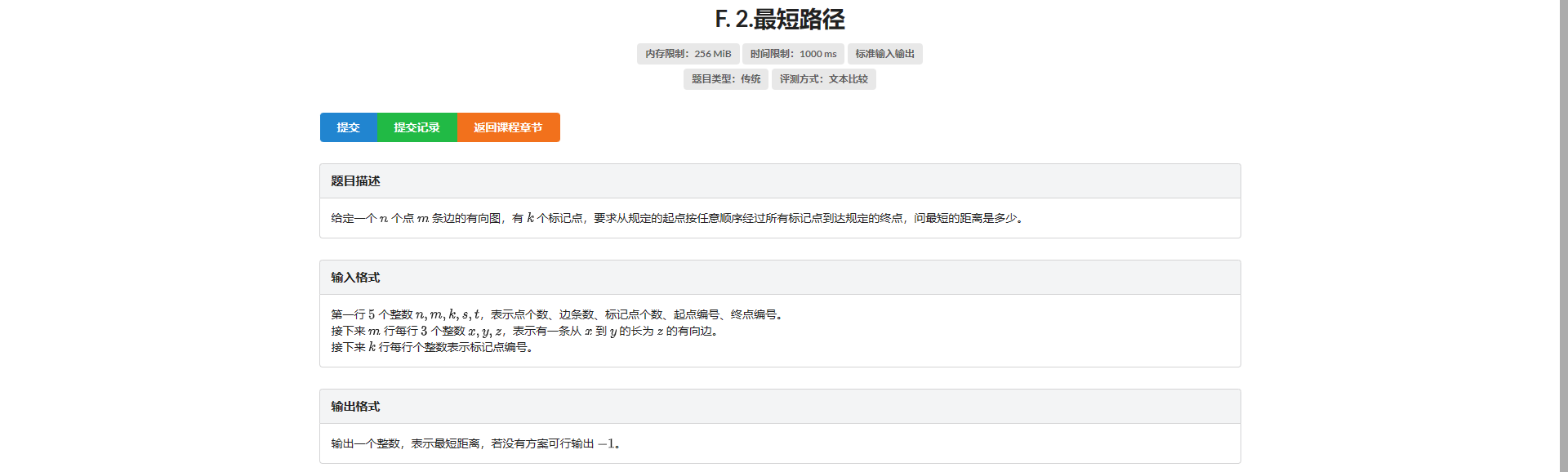
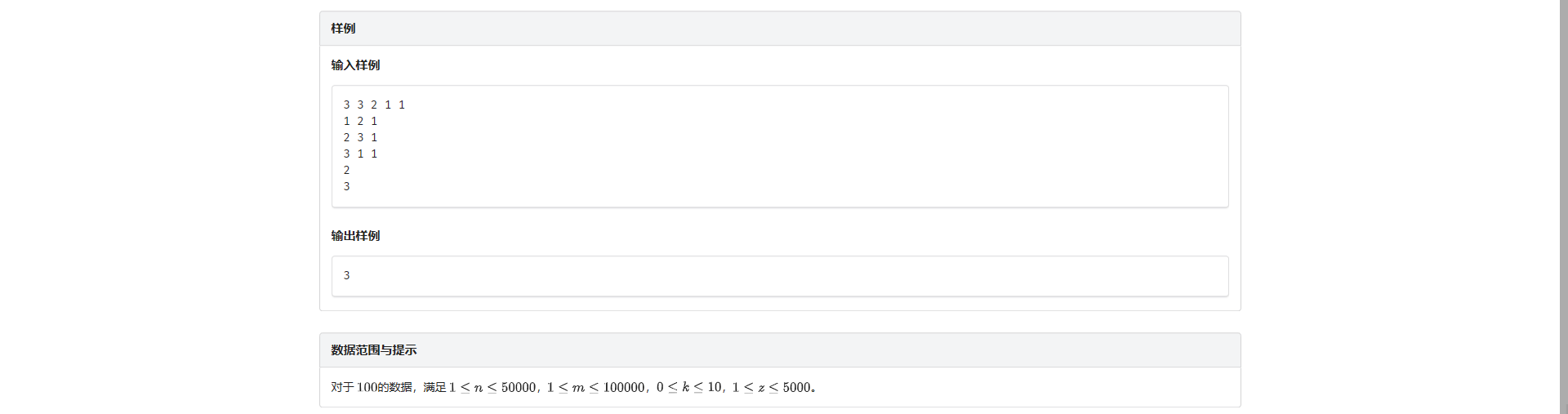
这是我在 ybt 里面见到的第几道最短路径了。。。
直接把起点和终点都加入特殊点然后跑哈密顿路即可
写的时候把 (s << 1) 写成了 (k << 1) 调了我15分钟 /fn
点击查看代码
#include <bits/stdc++.h>
#pragma GCC optimize(2)
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
if (x < 0) putchar('-'), x = -x;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
const int N = 5e4 + 0721;
const int M = 1e5 + 0721;
int head[N], nxt[M], to[M], len[M], cnt;
int sp[15];
ll dis[15][N], f[15][5210];
int n, m, k, S, T;
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
struct node {
int id;
ll dis;
friend bool operator<(node x, node y) {
return x.dis > y.dis;
}
};
priority_queue<node> q;
bool vis[N];
void dijkstra(int s, int id) {
memset(vis, 0, sizeof vis);
dis[id][s] = 0;
q.push((node){s, 0});
while (!q.empty()) {
int now = q.top().id;
q.pop();
if (vis[now]) continue;
vis[now] = 1;
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
if (dis[id][y] > dis[id][now] + len[i]) {
dis[id][y] = dis[id][now] + len[i];
q.push((node){y, dis[id][y]});
}
}
}
}
void main() {
n = read(), m = read(), k = read(), S = read(), T = read();
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= m; ++i) {
int x = read(), y = read(), z = read();
add_edge(x, y, z);
}
for (int i = 1; i <= k; ++i) {
int x = read();
sp[i] = x;
}
sp[0] = S;
++k;
sp[k] = T;
memset(dis, 0x3f, sizeof dis);
for (int i = 0; i <= k; ++i) dijkstra(sp[i], i);
f[0][1] = 0;
for (int i = 0; i <= (1 << k + 1) - 1; ++i) {
for (int j = 0; j <= k; ++j) {
for (int s = 0; s <= k; ++s) {
if (s == j) continue;
if ((i & (1 << j)) == 0) continue;
if ((i & (1 << s)) == 0) continue;
f[j][i] = min(f[j][i], f[s][i ^ (1 << j)] + dis[s][sp[j]]);
// cout << "dis: " << s << " " << sp[j] << " " << dis[s][sp[j]] << "\n";
// cout << j << " " << i << " " << s << " " << (i ^ (1 << j)) << " " << f[j][i] << "\n";
}
}
}
if (f[k][(1 << k + 1) - 1] < 0x3f3f3f3f3f3f3f3f) write(f[k][(1 << k + 1) - 1]), putchar('\n');
else puts("-1");
}
}
int main() {
steven24::main();
return 0;
}
/*
3 3 2 1 1
1 2 1
2 3 1
3 1 1
2
3
*/
G.小绿小蓝
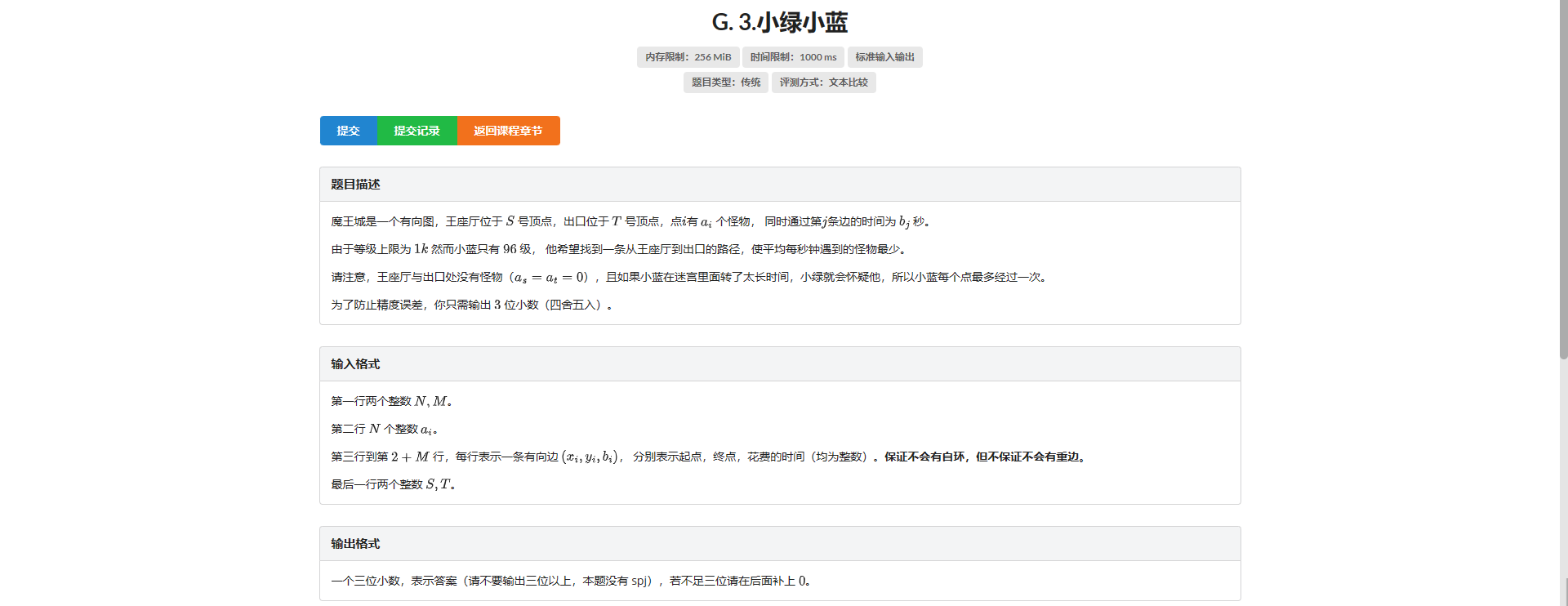
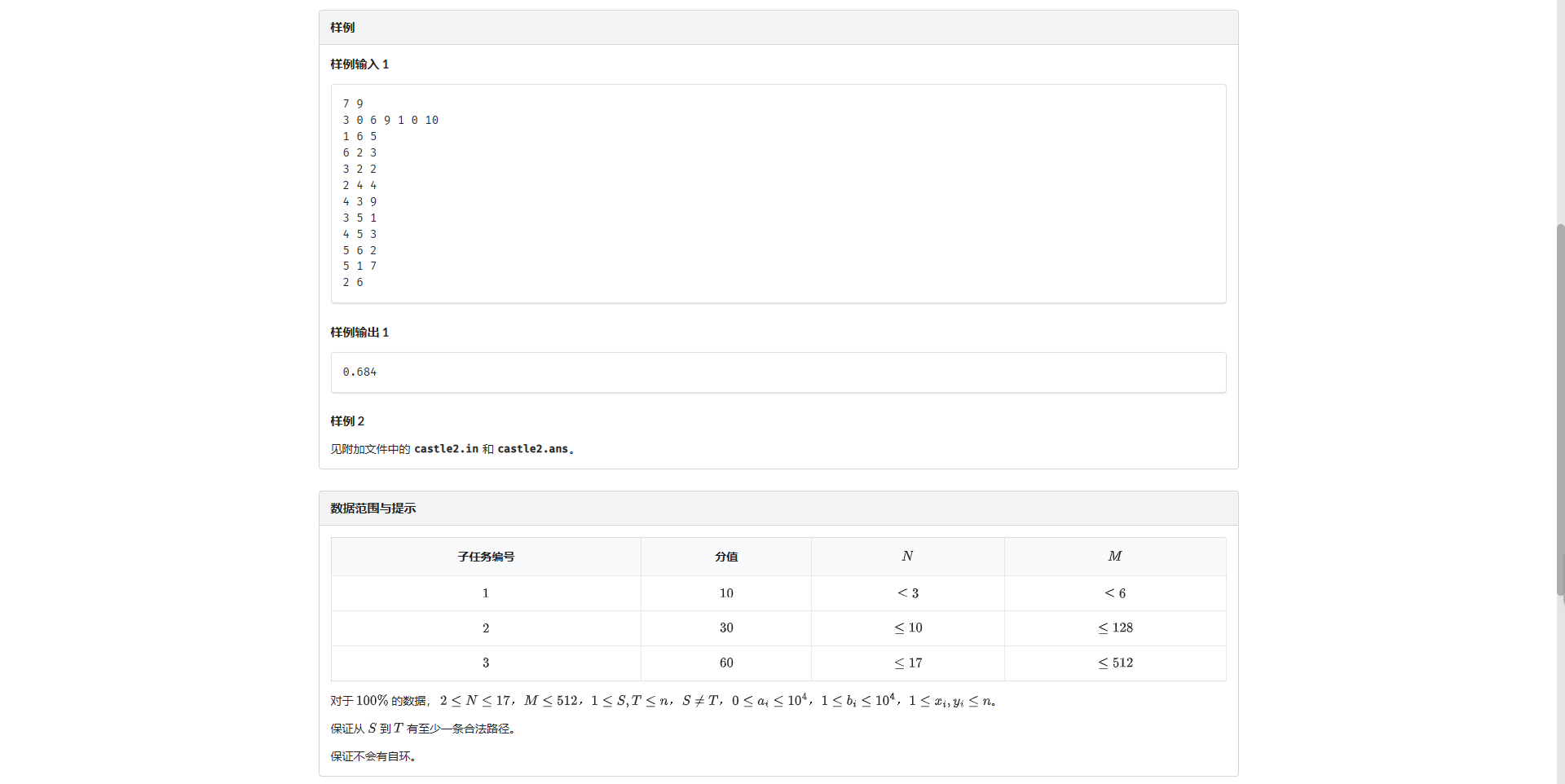
发现如果经过的点集固定 只需要最大化时间即可
所以直接跑哈密顿路求当前所有点经过情况为 \(S\) 的最长时间 最后枚举经过的点集统计答案即可
- 注意去重边
- 邻接表存图注意没有边连接的时候不能转移
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
if (x < 0) putchar('-'), x = -x;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
const int N = 2e5 + 0721;
const int M = 521;
const ll inf = 0x3f3f3f3f3f3f3f3f;
ll f[20][N];
int a[20];
int mp[20][20];
int n, m, S, T;
int calc(int s) {
int ret = 0;
for (int i = 1; i <= n; ++i) if (s & (1 << i - 1)) ret += a[i];
// cout << s << " " << ret
return ret;
}
void main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) a[i] = read();
for (int i = 1; i <= m; ++i) {
int x = read(), y = read(), z = read();
mp[x][y] = max(mp[x][y], z);
}
S = read(), T = read();
memset(f, -0x3f, sizeof f);
f[S][(1 << S - 1)] = 0;
for (int i = 0; i < (1 << n); ++i) {
for (int j = 1; j <= n; ++j) {
if (!(i & (1 << j - 1))) continue;
for (int k = 1; k <= n; ++k) {
if (j == k || !(i & (1 << k - 1))) continue;
if (!mp[k][j]) continue;
f[j][i] = max(f[j][i], f[k][i ^ (1 << j - 1)] + mp[k][j]);
}
}
}
double ans = 1e17;
for (int i = 0; i < (1 << n); ++i) {
if (f[T][i] <= 0) continue;
// cout << ans << "\n";
ans = min(ans, 1.0 * calc(i) / f[T][i]);
// cout << i << " " << f[T][i] << "\n";
}
printf("%.3lf", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
7 9
3 0 6 9 1 0 10
1 6 5
6 2 3
3 2 2
2 4 4
4 3 9
3 5 1
4 5 3
5 6 2
5 1 7
2 6
*/
H.擦除序列
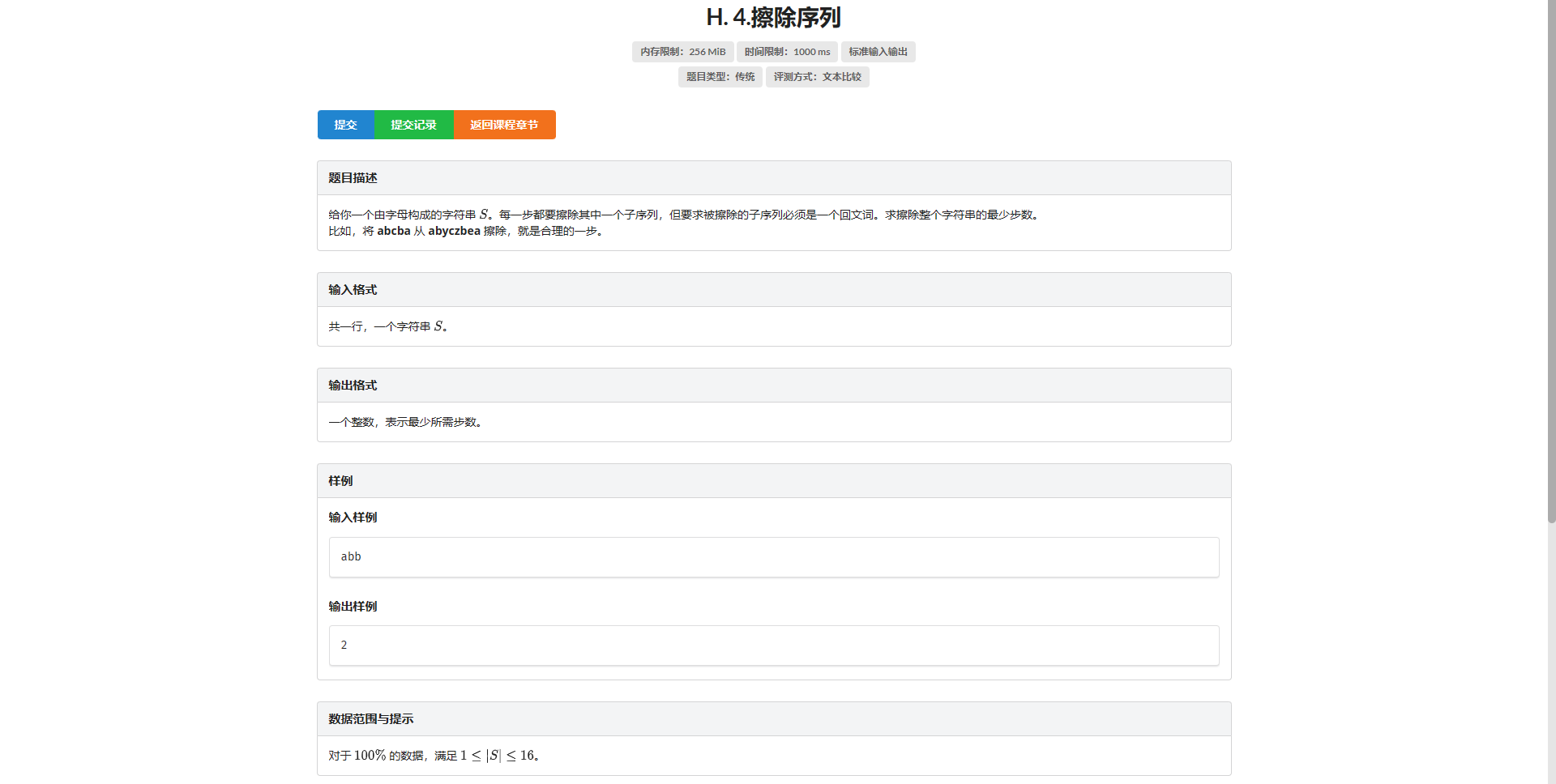
不难相当设 \(f_S\) 表示剩余字符集为 \(S\) 的最小步数
转移枚举子集显然
发现一个状态可能被判多次回文 所以判回文的时候记录一下保证不会TLE
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 1) + (xr << 3) + (cr ^ 48), cr = getchar();
return xr * F;
}
namespace steven24 {
const int N = 1e5 + 0721;
ll f[N];
int vis[N];
char tmp[21];
string s;
int n;
bool check(int S) {
if (vis[S] != -1) return vis[S];
int cnt = 0;
for (int i = 0; i < n; ++i) {
if (S & (1 << i)) tmp[++cnt] = s[i];
}
// for (int i = 1; i <= cnt; ++i) cerr << tmp[i];
// cerr << "\n";
for (int i = 1, j = cnt; i <= j; ++i, --j) {
if (tmp[i] != tmp[j]) return vis[S] = 0;
}
return vis[S] = 1;
}
void main() {
memset(vis, -1, sizeof vis);
cin >> s;
n = s.length();
memset(f, 0x3f, sizeof f);
f[(1 << n) - 1] = 0;
for (int i = (1 << n) - 1; i; --i) {
for (int j = i; j; j = (j - 1) & i) {
if (check(j)) f[i ^ j] = min(f[i ^ j], f[i] + 1);
}
}
// for (int i = 0; i < (1 << n); ++i) cerr << i << " " << vis[i] << "\n";
printf("%lld\n", f[0]);
}
}
int main() {
steven24::main();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号