YBTOJ 5.4树形DP
A.树上求和
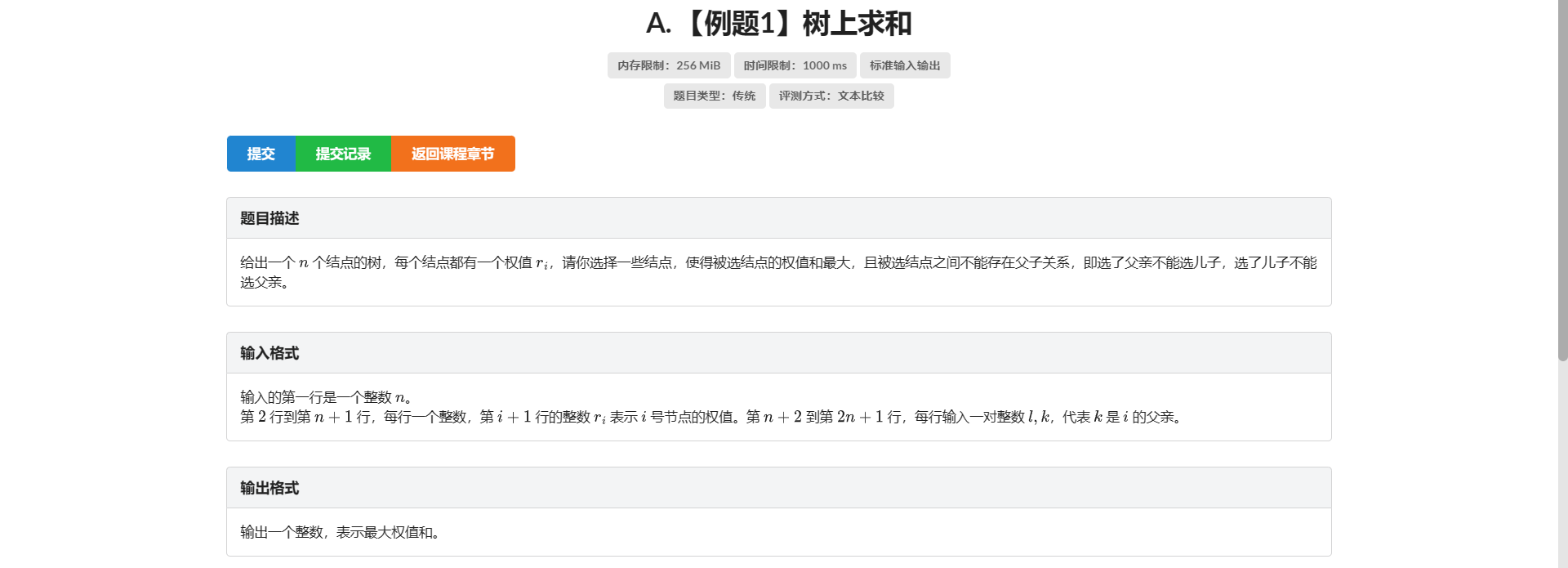
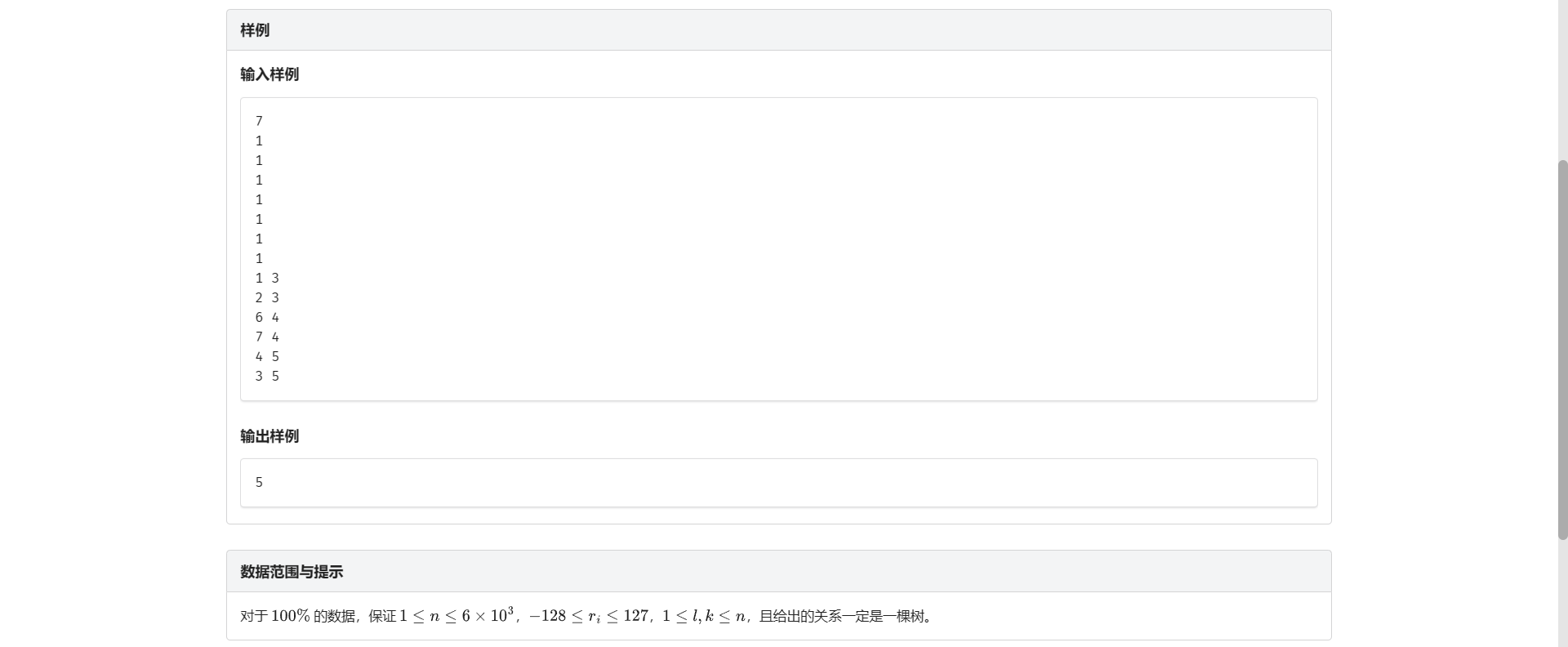
因为它有选/不选的状态 我们设状态的时候要考虑进去
所以设 \(f[i][0/1]\) 表示第 \(i\) 个节点没选/选的最大价值
显然就有:
- \(f[fa][0] = \sum max(f[son][0], f[son][1])\)
- \(f[fa][1] = \sum f[son][0]\)
因为父亲的状态要从儿子转移过来 所以先递归后转移
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 0721;
int head[N], to[N], nxt[N], cnt;
int f[N][2];
bool rt[N];
int n, root;
inline void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
dfs(y);
f[x][0] += max(f[y][0], f[y][1]);
f[x][1] += f[y][0];
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &f[i][1]);
for (int i = 1; i < n; ++i) {
int fa, son;
scanf("%d%d", &son, &fa);
cmb(fa, son);
rt[son] = 1;
}
for (int i = 1; i <= n; ++i) {
if (!rt[i]) {
root = i;
break;
}
}
dfs(root);
printf("%d", max(f[root][0], f[root][1]));
return 0;
}
B.节点覆盖
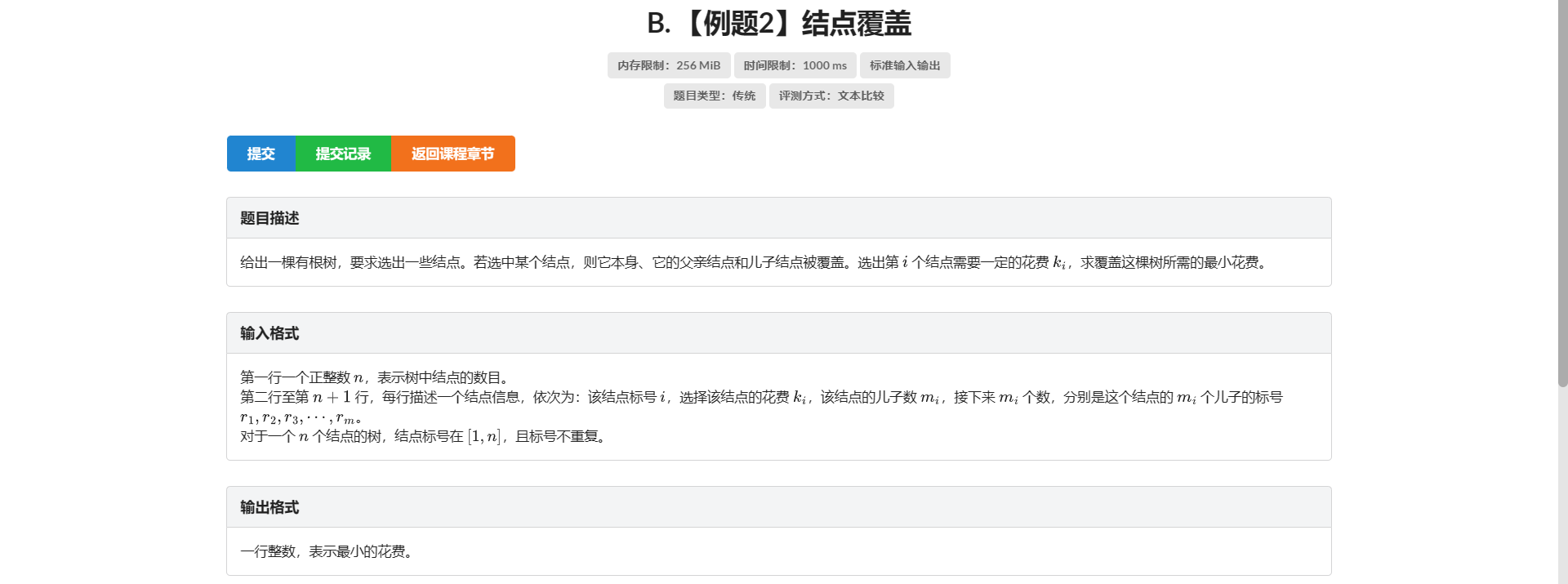
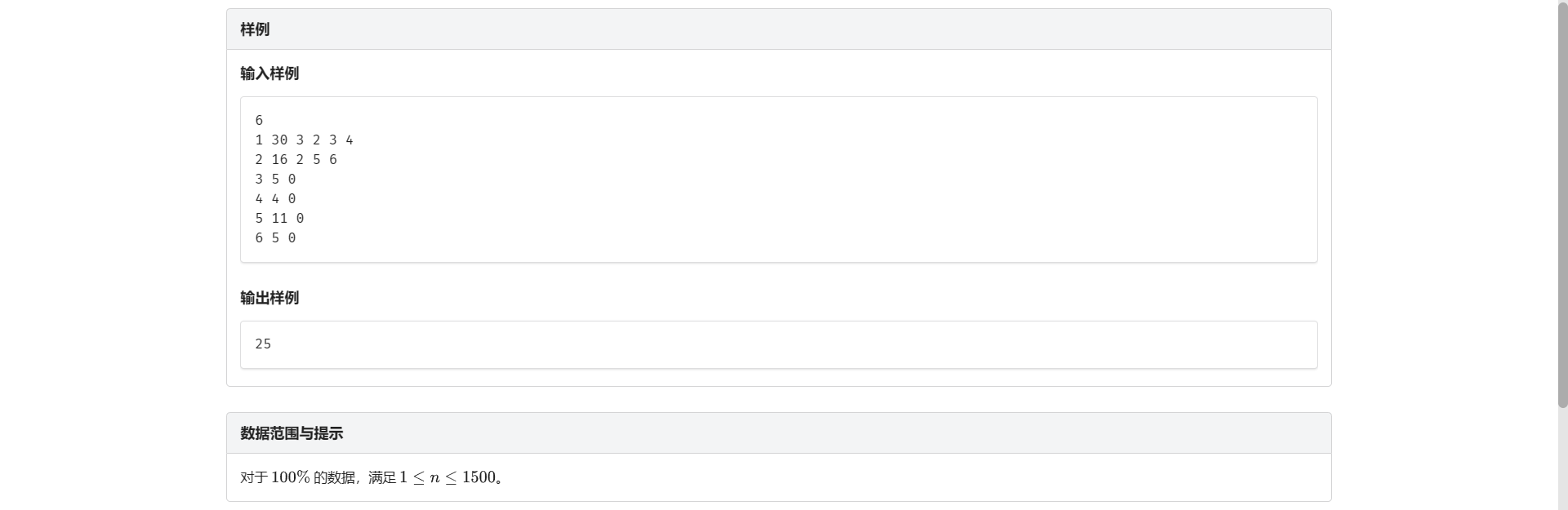
很容易想到的一个思路是用 \(1/0\) 表示选/不选这个节点
但是有一个问题 转移的时候它的父亲和它的儿子必须满足至少选一个 没法转移
所以我们考虑设 \(0/1/2\) 表示被父亲/自己/儿子看守
转移很显然 可以看代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 0x0d00;
int head[N], nxt[N], to[N], v[N];
int dp[N][3];
int cnt, n, ans;
void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int fa) {
dp[x][1] = v[x];
int tmp = 0x7ffffff;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa)
continue;
dfs(y, x);
tmp = min(tmp, dp[y][1] - dp[y][2]);
dp[x][0] += min(dp[y][1], dp[y][2]);
dp[x][1] += min(dp[y][0], min(dp[y][1], dp[y][2]));
dp[x][2] += min(dp[y][1], dp[y][2]);
}
dp[x][2] += max(tmp, 0);
if (fa == 0)
ans = min(dp[x][1], dp[x][2]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int x, m;
cin >> x;
cin >> v[x];
cin >> m;
if (m != 0) {
for (int j = 1; j <= m; ++j) {
int u;
scanf("%d", &u);
cmb(x, u);
cmb(u, x);
}
}
}
// cout<<cnt ;
dfs(1, 0);
// for( int i = 1 ; i <= cnt ; ++i )
// cout<<to[i]<<" " ;
printf("%d", ans);
return 0;
}
C.最长距离
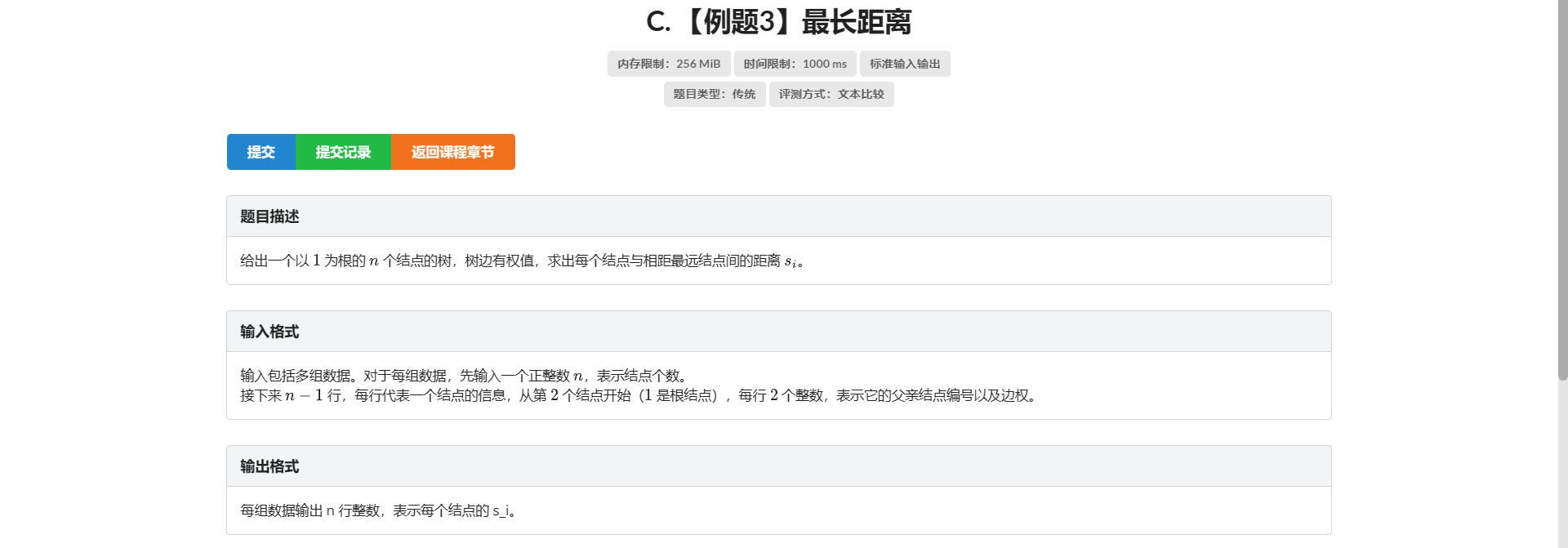
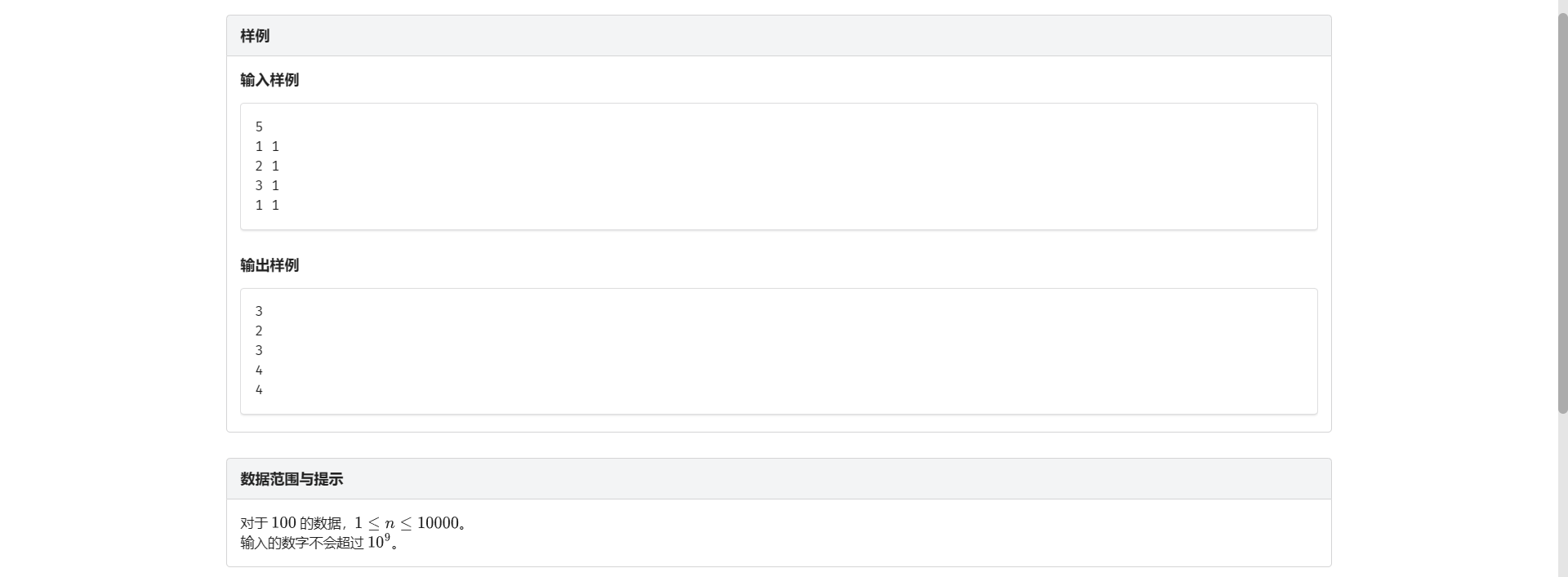
D.选课方案
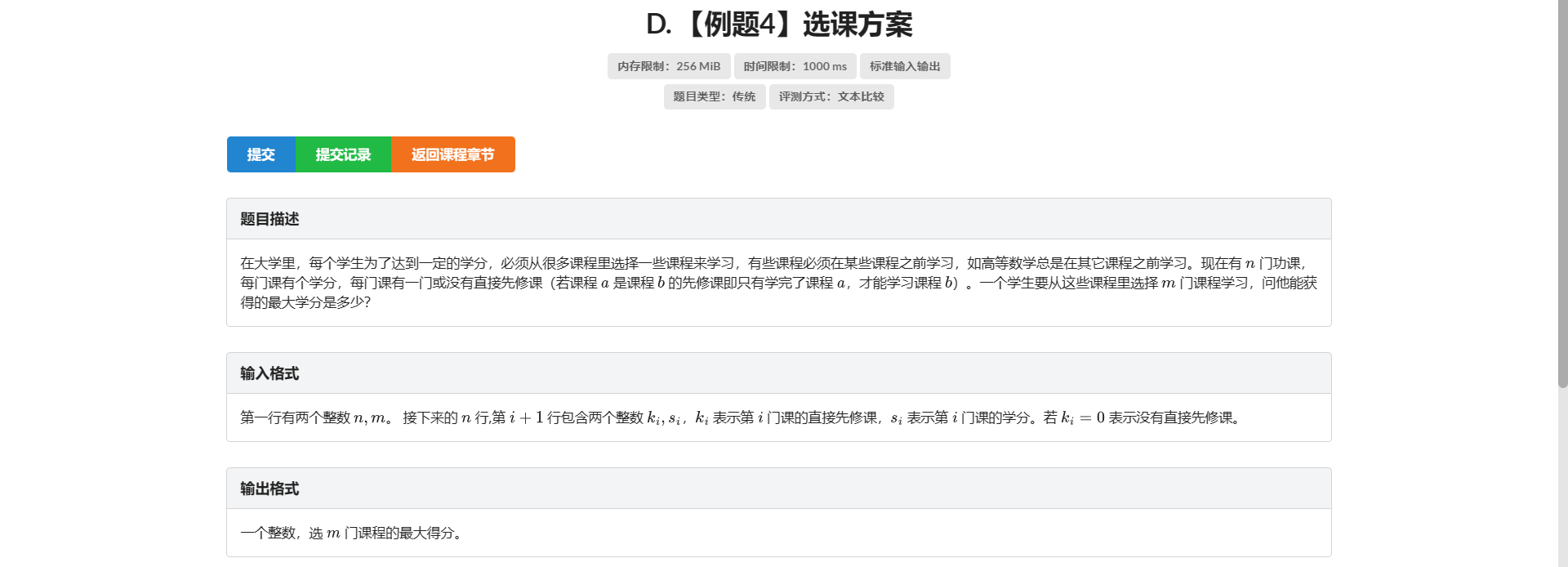
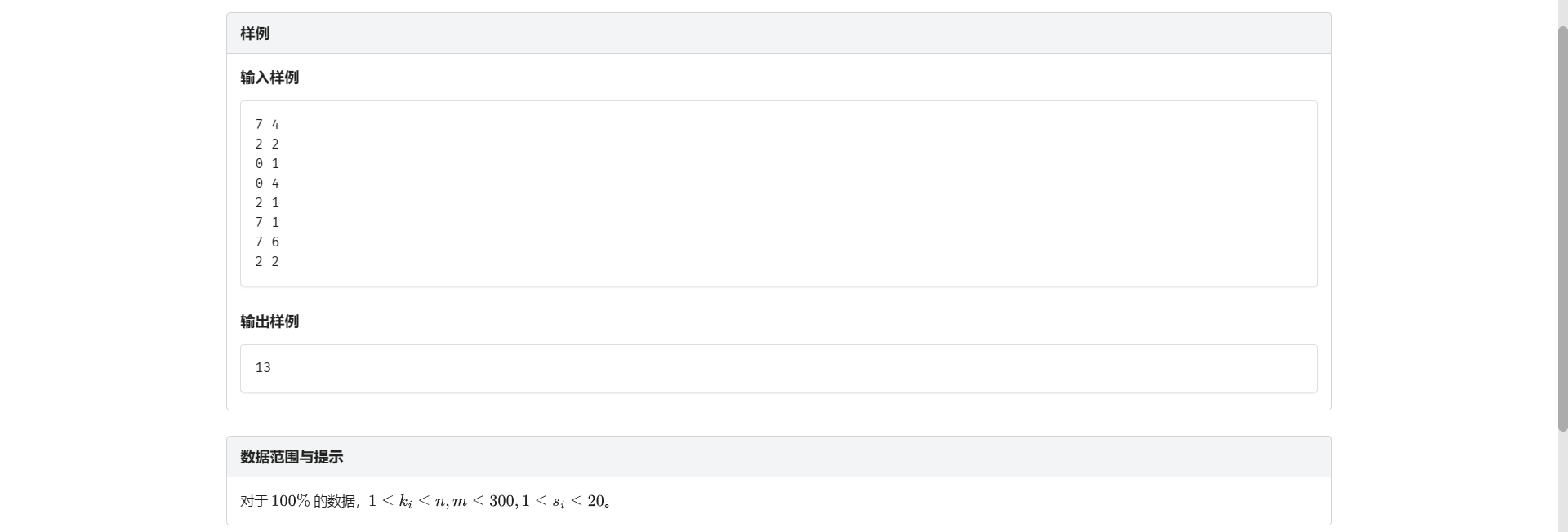
详见P2014 选课 ( 树上背包 )
复杂度证明是假的不要看
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 0721;
int head[N], nxt[N], to[N], cnt;
int dp[N][N];
int m, n;
void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
dfs(y);
for (int j = m + 1; j > 0; --j) {
for (int k = 0; k < j; ++k) dp[x][j] = max(dp[x][j], dp[x][j - k] + dp[y][k]);
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
cmb(x, i);
for (int j = 1; j <= m + 1; ++j) dp[i][j] = y;
}
dfs(0);
printf("%d", dp[0][m + 1]);
return 0;
}
E.路径求和
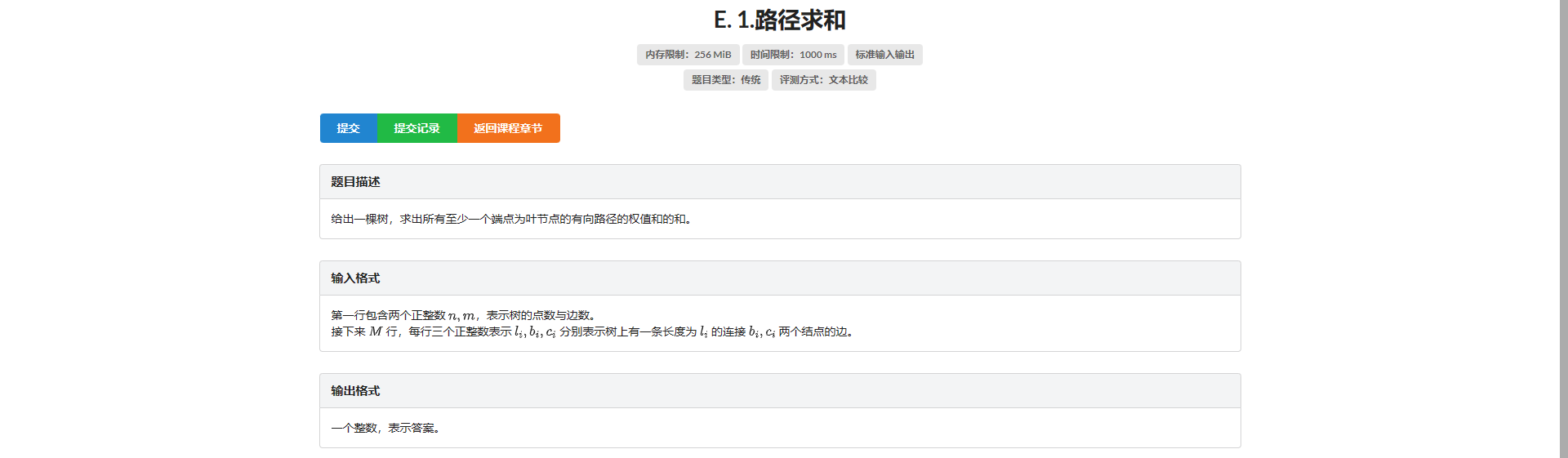
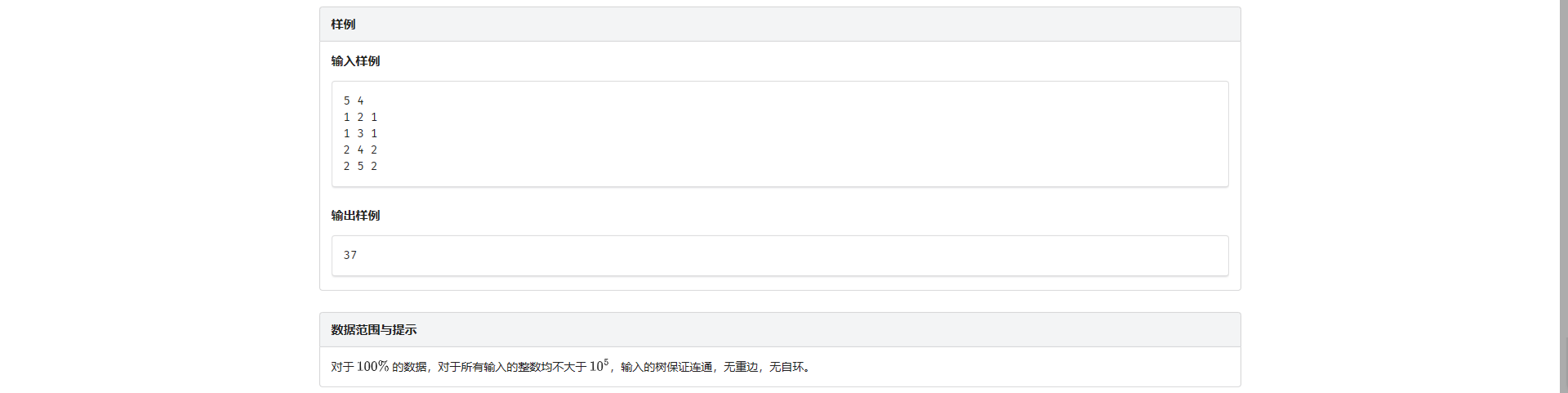
很适合独立思考的一道题 但是题面没看懂直接去找题解了 可惜了
应该加上一句话:对于无根树 我们定义度数为 \(1\) 的点为叶节点
暴力的想法是枚举点对 \(\text{O}(n ^ 2)\)
考虑每一条边对答案的贡献 把它断掉把树分为两个子树 \(x, y\)
那么这条边对答案的贡献就是 \(x\) 中的所有叶节点走到 \(y\) 中的所有节点 + \(y\) 中的所有叶节点走到 \(x\) 中的所有节点
所以我们直接维护出每个子树的大小以及叶节点数量即可
理论上要把 \(deg_i \neq 1\) 的 \(i\) 作根节点开始 dfs
但实际这题直接 dfs(1, 0) 也能过
注意本题是先输入边权再输入两端点 /fn
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
int head[N], to[N << 1], nxt[N << 1], len[N << 1], cnt;
int deg[N], siz[N], num[N];
int totleaf;
int n, m;
ll ans;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
void dfs(int x, int fa) {
siz[x] = 1;
if (deg[x] == 1) {
++totleaf;
num[x] = 1;
}
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
dfs(y, x);
siz[x] += siz[y];
num[x] += num[y];
}
}
void get_ans(int x, int fa) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
ans += 1ll * len[i] * (1ll * num[y] * (n - siz[y]) + 1ll * siz[y] * (totleaf - num[y]));
get_ans(y, x);
}
}
void main() {
n = read(), m = read();
// cerr << n << " " << m << "\n";
for (int i = 1; i <= m; ++i) {
int x, y, z;
z = read(), x = read(), y = read();
// cerr << x << " " << y << " " << z << "\n";
add_edge(x, y, z);
add_edge(y, x, z);
++deg[x], ++deg[y];
}
for (int i = 1; i <= n; ++i) {
if (deg[i] > 1) {
dfs(i, 0);
get_ans(i, 0);
break;
}
}
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
5 4
1 2 1
1 3 1
2 4 2
2 5 2
*/
F.树上移动
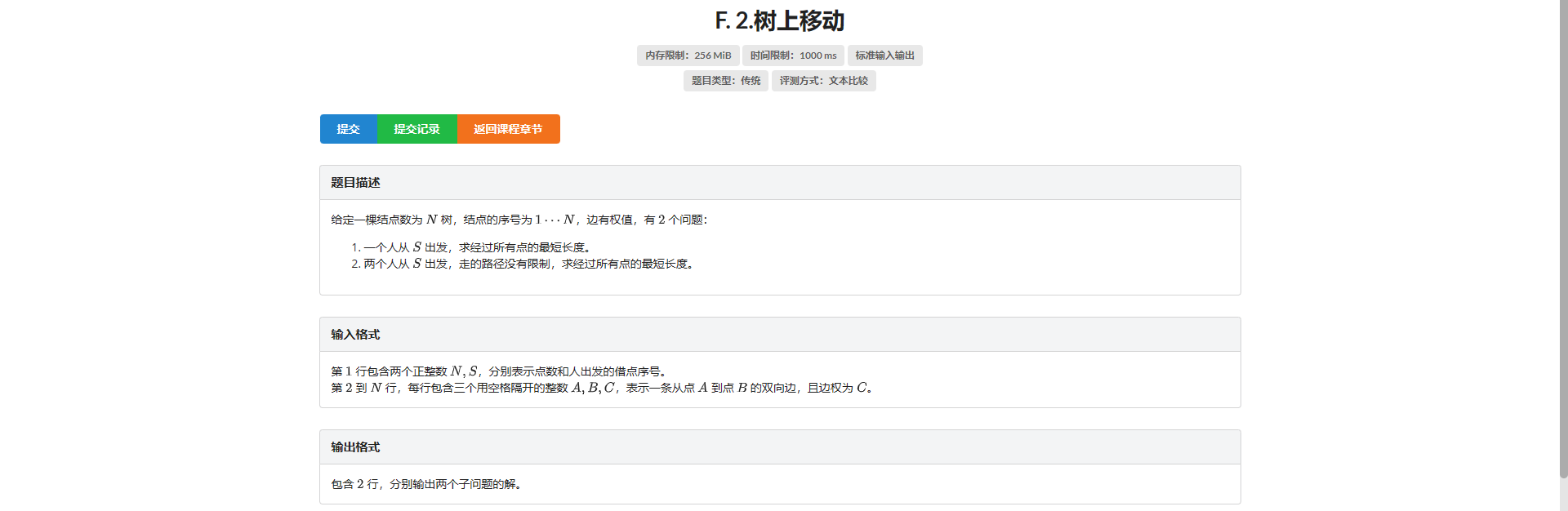
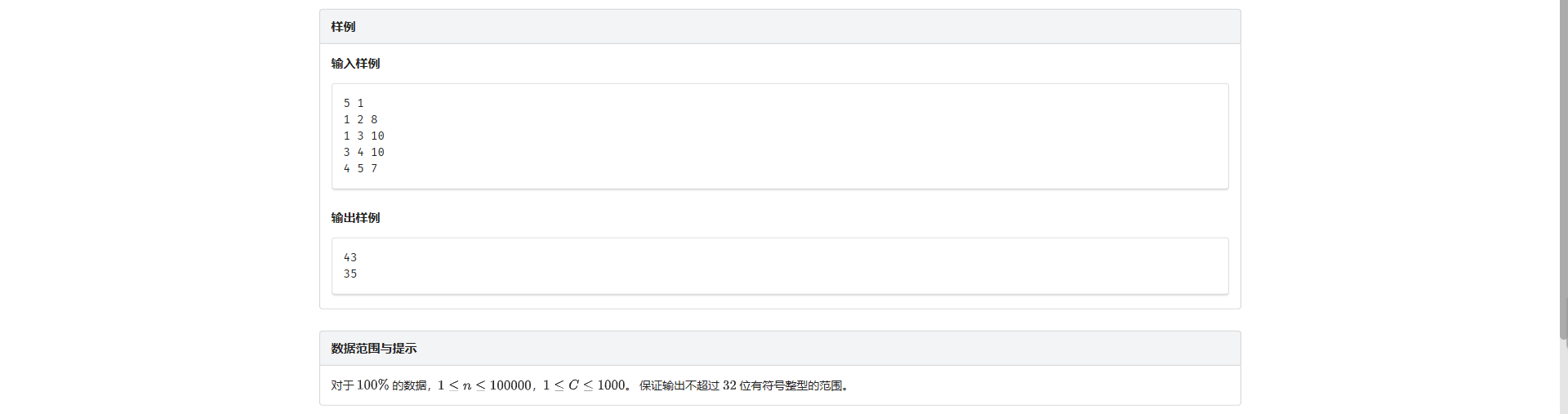
无根树 并且 \(S\) 是固定的 不难想到把 \(S\) 作为根节点
设 \(f_{i, 0/1/2}\) 表示从 \(i\) 出发遍历子树内所有节点 回到 / 一个点出发不回到 / 两个点出发不回到该节点的最短距离
转移的时候 对于 \(f_{x, 0}\) 有 \(f_{x, 0} = \sum\limits_{y \in son_x} f_{y, 0} + 2 \times dis_{x, y}\)
对于 \(f_{x, 1}\) 有 \(f_{x, 1} = \min\limits_{y \in son_x}(f_{y, 1} + dis_{x, y} + \sum\limits_{z \in son_x, z \ne y} f_{z, 0} + 2 \times dis_{x, z})\)
对于第二个转移 我们把 \(\sum\limits_{z \in son_x, z \ne y} f_{z, 0} + 2 \times dis_{x, z}\) 转化成 \(f_{x, 0} - f_{y, 0} - dis_{x, y} \times 2\) 来保证复杂度
对于 \(f_{x, 2}\) 可以是一个儿子的 \(f_{y, 2} + 2 \times dis_{x, y}\) + 剩余儿子的 \(f_{y, 0} + 2 \times dis_{x, y}\)
也可以是两个儿子的 \(f_{y, 1}\) + 剩余儿子的 \(f_{y, 0} + 2 \times dis_{x, y}\)
前面那个转移还是用上面那个优化来保证复杂度
对于下面那个 我们考虑取到 \(f_{y, 1}\) 与 \(f_{x, 0}\) 的差值 那就是 \(f_{x, 0} - f_{y, 0} + f_{y, 1} - dis_{x, y}\)
那么我们直接维护 $ - f_{y, 0} + f_{y, 1} - dis_{x, y}$ 的最小值和次小值即可
那么对于第一问 答案就是 \(f_{s, 1}\)
对于第二问 答案就是 \(f_{s, 2}\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
const ll inf = 0x7ffffffffffffff;
int head[N], to[N << 1], nxt[N << 1], len[N << 1], cnt;
ll f[N][3];
int n, s;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
void dfs(int x, int fa) {
bool isleaf = 1;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
isleaf = 0;
dfs(y, x);
f[x][0] += f[y][0] + 2 * len[i];
}
if (!isleaf) {
f[x][1] = inf;
f[x][2] = inf;
}
ll min1 = inf, min2 = inf;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
f[x][1] = min(f[x][1], f[y][1] - len[i] + f[x][0] - f[y][0]);
f[x][2] = min(f[x][2], f[y][2] + f[x][0] - f[y][0]);
if (f[y][1] - f[y][0] - len[i] < min1) {
min2 = min(min2, min1);
min1 = f[y][1] - f[y][0] - len[i];
} else min2 = min(min2, f[y][1] - f[y][0] - len[i]);
}
if (min1 != inf && min2 != inf) f[x][2] = min(f[x][2], f[x][0] + min1 + min2);
}
void main() {
n = read(), s = read();
for (int i = 1; i < n; ++i) {
int x, y, z;
x = read(), y = read(), z = read();
add_edge(x, y, z);
add_edge(y, x, z);
}
dfs(s, 0);
printf("%lld\n", f[s][1]);
printf("%lld\n", f[s][2]);
}
}
int main() {
steven24::main();
return 0;
}
/*
5 1
1 2 8
1 3 10
3 4 10
4 5 7
*/
G.块的计数
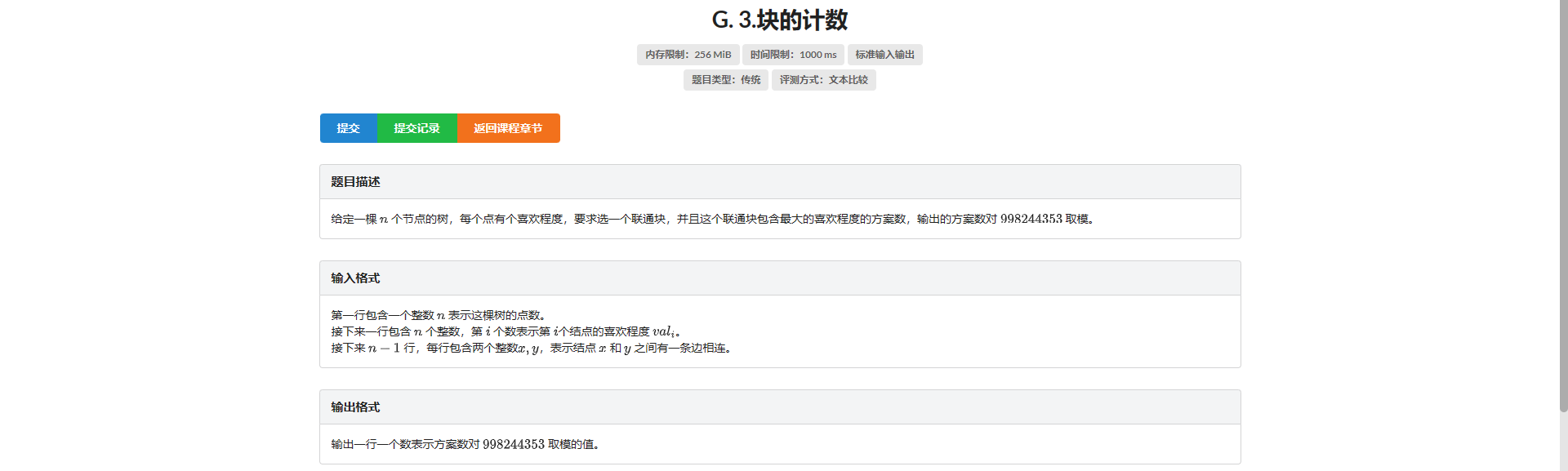
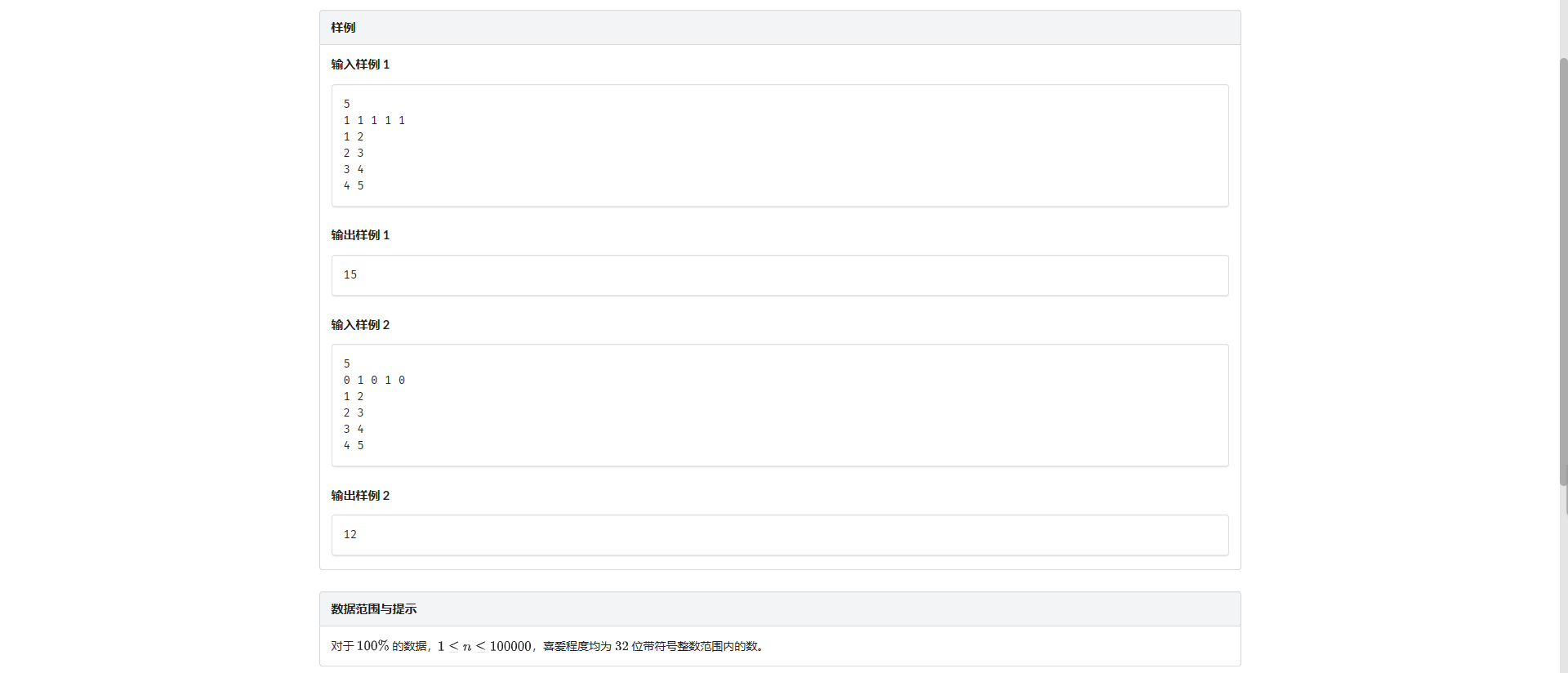
设 \(f_{i, 0/1}\) 表示以 \(i\) 为根节点的合法 / 不合法联通块个数
下意识觉得不合法联通块个数不是很好转移
进而考虑设 \(f_{i, 0/1}\) 表示以 \(i\) 为根节点的合法 / 合不合法都行的联通块个数 剩下那个减一下就行了
然后写假了 寄。
实际上不好转移的是合法连通块个数
所以设 \(f_{i, 0/1}\) 表示以 \(i\) 为根节点的不合法 / 合不合法都行的连通块个数
那么就有 \(f_{x, 0} = \prod\limits_{y \in son_x} (f_{y, 0} + 1)\) (可以不选)
\(f_{x, 1} = \prod\limits_{y \in son_x} (f_{y, 1} + 1)\) (可以不选)
答案就是 \(\sum\limits_{i = 1}^n (f_{i, 1} - f_{i, 0})\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
const int mod = 998244353;
ll f[N][2];
int val[N], maxn;
int head[N], nxt[N << 1], to[N << 1], cnt;
int n;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int fa) {
f[x][1] = 1;
if (val[x] != maxn) f[x][0] = 1;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
dfs(y, x);
f[x][1] = f[x][1] * (f[y][1] + 1) % mod;
f[x][0] = f[x][0] * (f[y][0] + 1) % mod;
}
}
void main() {
n = read();
for (int i = 1; i <= n; ++i) val[i] = read();
maxn = *max_element(val + 1, val + 1 + n);
for (int i = 1; i < n; ++i) {
int x, y;
x = read(), y = read();
add_edge(x, y);
add_edge(y, x);
}
dfs(1, 0);
ll ans = 0;
for (int i = 1; i <= n; ++i) ans = (mod + ans + f[i][1] - f[i][0]) % mod;
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
5
1 1 1 1 1
1 2
2 3
3 4
4 5
*/
H.树的合并
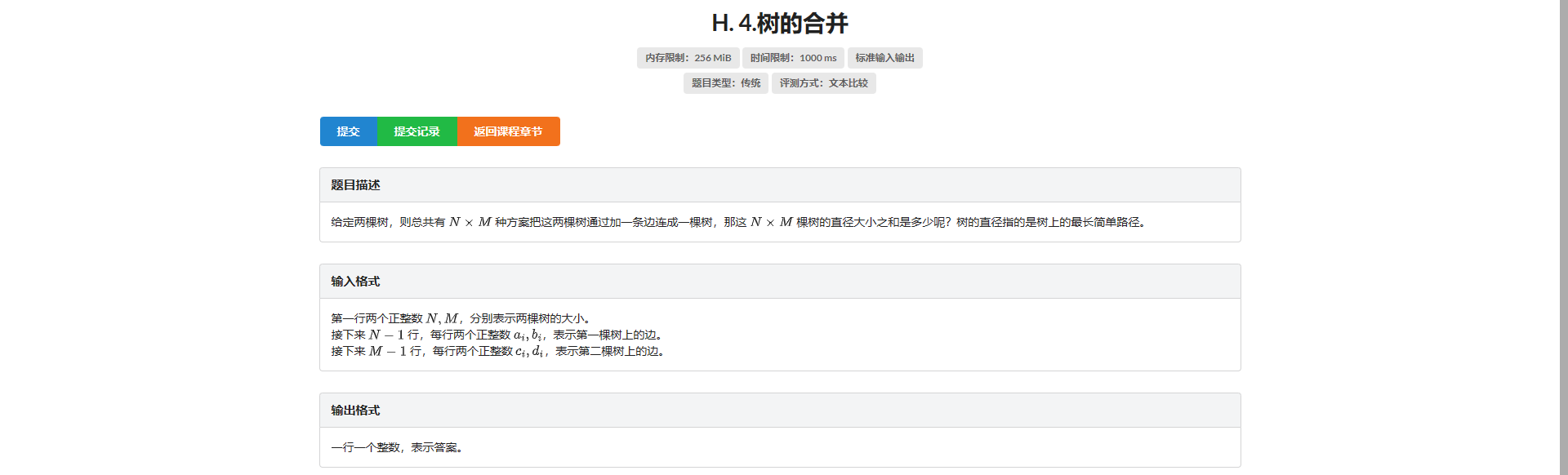
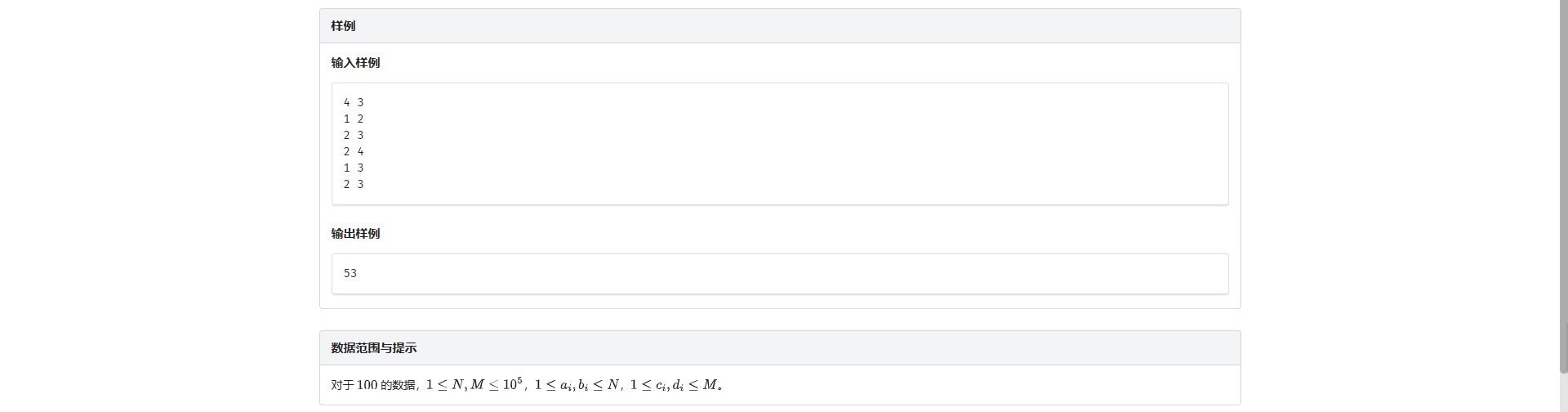
考虑枚举第一颗树上的点 把它们和第二颗树上所有点连边的情况
设两点为 \(u, v\) 设 \(f_i\) 表示 \(i\) 在它所在树里能走到的最远点距离
那么显然新树直径就是 \(\max(第一棵树直径, 第二棵树直径, f_u + f_v + 1)\)
我们枚举 \(u\) 点 那么我们就需要讨论 \(f_u + f_v + 1\) 与 \(\max(第一棵树直径, 第二棵树直径)\) 的大小
\(f_u\) 是给定的 那么如果我们把 \(f_v\) 排序 我们就可以二分一个位置 使它前面的 \(v\) 都取 \(\max(第一棵树直径, 第二棵树直径)\) 后面的 \(v\) 都取 \(f_u + f_v + 1\)
那么前面那些直接就是点数 \(\times \max(第一棵树直径, 第二棵树直径)\)
后面那些预处理一个后缀和即可
总复杂度 \(\text{O}(n \log n + n \log m + m \log m)\)
如果用 C 题那个做法来预处理 \(f\) 数组的话就是 \(\text{O}(n \log m + m \log m)\)
然后如果 \(m > n\) 的话就把两棵树 swap 一下 就可以做到极致复杂度 虽然最开始那个复杂度就随便过了(
注意二分边界为 \(\left[1, m + 1\right]\) 炸了一发
点击查看代码
/*
两次dfs求出直径两端点
维护树上距离
求出每个点的最长距离 然后全拿下来放到两个数组里
在b中二分找f[i] + g[j] + 1>max(d1, d2)的最小j
给g弄个后缀和
ans+=max(d1,d2)*(j-1)+h[j]+(f[i]+1)*(n2-j+1)
*/
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
if (x < 0) putchar('-'), x = -x;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
const int N = 1e5 + 0721;
int f[N], g[N];
ll h[N], ans;
int d;
struct tree {
int dis[N], dep[N], fa[21][N];
int head[N], nxt[N << 1], to[N << 1], cnt;
int u1, u2, d;
int n;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs1(int x, int f) {
dep[x] = dep[f] + 1;
fa[0][x] = f;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == f) continue;
dfs1(y, x);
}
}
void dfs2(int x, int f, bool opt) {
dis[x] = dis[f] + 1;
if (!opt) {
if (dis[x] > dis[u1]) u1 = x;
}
else {
if (dis[x] > dis[u2]) u2 = x;
}
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == f) continue;
dfs2(y, x, opt);
}
}
void init() {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) fa[j][i] = fa[j - 1][fa[j - 1][i]];
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (int j = 20; j >= 0; --j) if (dep[fa[j][x]] >= dep[y]) x = fa[j][x];
if (x == y) return x;
for (int j = 20; j >= 0; --j) if (fa[j][x] != fa[j][y]) x = fa[j][x], y = fa[j][y];
return fa[0][x];
}
int query(int x, int y) {
return dep[x] + dep[y] - (dep[lca(x, y)] << 1);
}
} tr1, tr2;
void init(tree &x) {
x.dfs1(1, 0);
x.init();
x.dfs2(1, 0, 0);
memset(x.dis, 0, sizeof x.dis);
x.dfs2(x.u1, 0, 1);
x.d = x.query(x.u1, x.u2);
}
int binary_search(int val, int l, int r) {
int mid, ret = -1;
while (l <= r) {
mid = (l + r) >> 1;
if (g[mid] + val + 1 > d) {
ret = mid;
r = mid - 1;
} else
l = mid + 1;
}
if (ret == -1) return r + 1;
else return ret;
}
void main() {
tr1.n = read(), tr2.n = read();
int n1 = tr1.n, n2 = tr2.n;
for (int i = 1; i < n1; ++i) {
int x = read(), y = read();
tr1.add_edge(x, y);
tr1.add_edge(y, x);
}
for (int i = 1; i < n2; ++i) {
int x = read(), y = read();
tr2.add_edge(x, y);
tr2.add_edge(y, x);
}
init(tr1);
init(tr2);
for (int i = 1; i <= n1; ++i) f[i] = max(tr1.query(i, tr1.u1), tr1.query(i, tr1.u2));
for (int i = 1; i <= n2; ++i) g[i] = max(tr2.query(i, tr2.u1), tr2.query(i, tr2.u2));
sort(g + 1, g + 1 + n2);
for (int i = n2; i; --i) h[i] = h[i + 1] + g[i];
d = max(tr1.d, tr2.d);
for (int i = 1; i <= n1; ++i) {
int loc = binary_search(f[i], 1, n2);
ans += 1ll * d * (loc - 1) + h[loc] + 1ll * (f[i] + 1) * (n2 - loc + 1);
}
write(ans), putchar('\n');
}
}
int main() {
steven24::main();
return 0;
}
/*
4 3
1 2
2 3
2 4
1 3
2 3
*/
I.权值统计
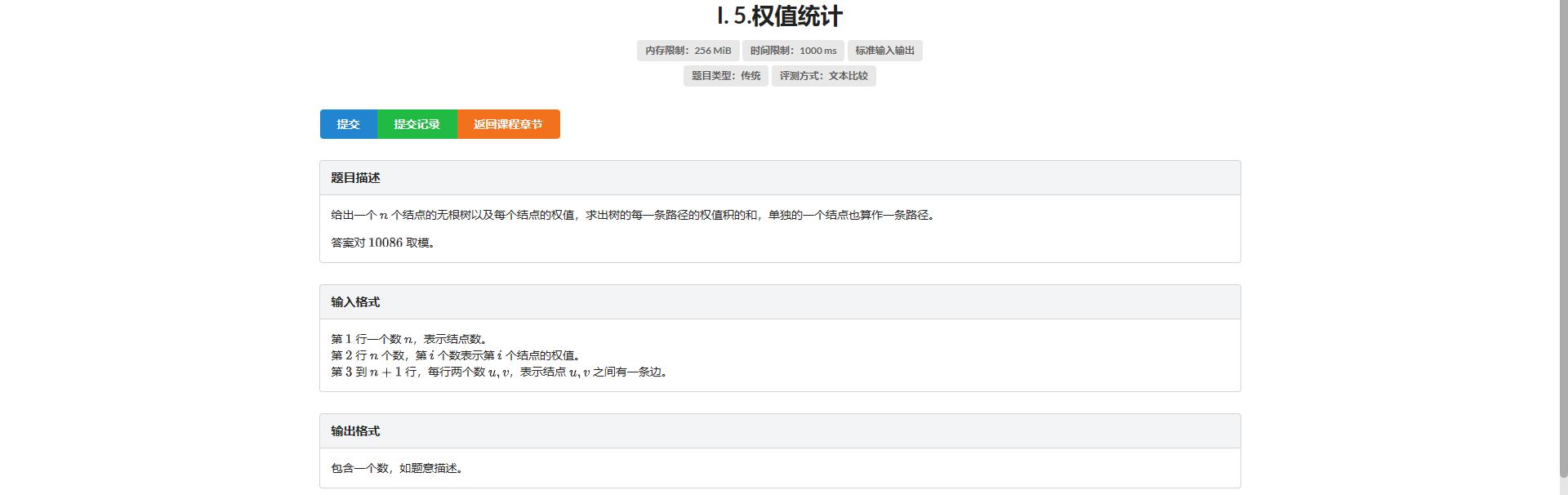
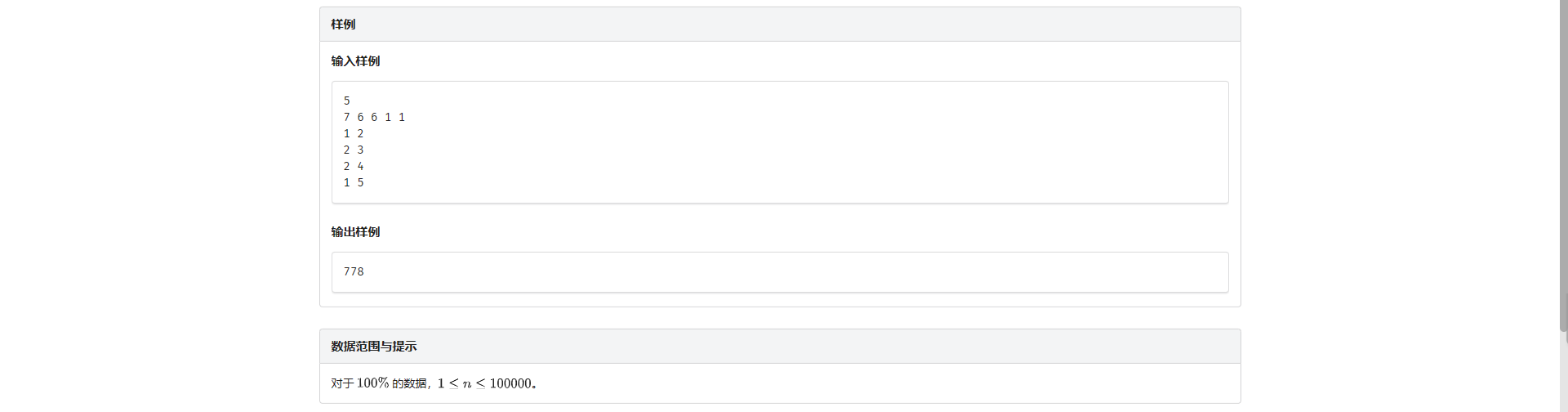
想到个换根的做法结果被卡模数 怎么会是呢
设 \(f_i\) 表示以 \(i\) 为根的子树内所有以 \(i\) 为终点的路径权值和
设 \(g_i\) 表示以 \(i\) 为根的子树内所有经过 \(i\) 的路径权值和
考虑转移
对于 \(f_i\) 显然就是所有以它儿子为终点的路径都加上它自己 还有只包含它自己一个点的路径
有 \(f_i = (\sum\limits f_{son_i} + 1) \times v_i\)
对于 \(g_i\) 需要额外统计从一个子树出来经过 \(i\) 再进入另一个子树的路径权值和
实际上这部分就是 \((\sum\limits 儿子的f值两两相乘) \times v_i\) 具体可以自己拆一下
注意到 \(2(x_1x_2 + x_2x_3 + x_1x_3) = (x_1 + x_2 + x_3) ^ 2 - (x_1^2 + x_2^2 + x_3^2)\) 并且这个柿子对于更多的 \(x_i\) 也成立
所以就可以换成 \(\frac{(\sum\limits f_{son_i})^2 - \sum\limits f_{son_i}^2}{2}\)
那么就有 \(g_i = f_i + \frac{(\sum\limits f_{son_i})^2 - \sum\limits f_{son_i}^2}{2} \times v_i\)
最终答案为 \(\sum\limits_{i=1}^n g_i\)
点击查看代码
/*
*/
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
if (x < 0) putchar('-'), x = -x;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
const int N = 1e5 + 0721;
const int mod = 10086;
ll f[N];
int v[N];
int head[N], nxt[N << 1], to[N << 1], cnt;
int n;
ll ans;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int fa) {
ll sum = 0, tot = 0;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
dfs(y, x);
sum += f[y];
tot += f[y] * f[y];
}
f[x] = 1ll * (sum + 1) * v[x] % mod;
ans = (ans + f[x] + (sum * sum - tot) / 2 * v[x]) % mod;
}
void main() {
n = read();
for (int i = 1; i <= n; ++i) v[i] = read();
for (int i = 1; i < n; ++i) {
int x = read(), y = read();
add_edge(x, y);
add_edge(y, x);
}
dfs(1, 0);
write(ans), putchar('\n');
}
}
int main() {
steven24::main();
return 0;
}
/*
4 3
1 2
2 3
2 4
1 3
2 3
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号