YBTOJ 5.3数位DP
来自神 wind_whisper 的一句话

A.B数计数
问是否能被 \(13\) 整除和是否包含 \(13\) 考虑加上这两维信息
设 \(f[pos][mod][k]\) 表示在 \(pos\) 位 当前模数为 \(mod\) 含 \(13\) 的状态为 \(k\)
其中 \(k = 2\) 表示已经有 \(13\) \(k = 1\) 表示当前位有 \(3\) \(k = 0\) 表示啥也没有
考虑转移 首先对于模数问题 我们假设当前位的数为 \(i\)
那么当前位的 \(mod\) 由原来 \((mod + power[wei - 1] * i) mod 13\) 得到
那么逆推回去 原来的 \(mod\) 就是当前 \(mod - power[wei - 1] * i\)
然后考虑含 \(13\) 状态的转移:
- 当 \(k = 0\) 时 首先这一位不能填 \(3\) 它可以是由上一位 \(k = 0\) 填任何数转移过来
也可能是由上一位 \(k = 1\) 但是这一位没有填 \(1\) 转移过来 - 当 \(k = 1\) 时 显然只能是上一位 \(k \neq 2\) 并且这一位填 \(3\) 转移过来
- 当 \(k = 2\) 时 可以是由上一位 \(k = 2\) 填任何数
或者上一位 \(k = 1\) 并且这一位填 \(1\)
还需要开个 \(lim\) 表示之前是否填的都是最高位 那么这一位的枚举就要有限制
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int f[11][13][3], power[10], n;
void init() {
power[0] = 1;
for (int i = 1; i <= 9; ++i) power[i] = power[i - 1] * 10;
}
int dp(int wei, int mod, int pos, bool lim) {
if (!lim && f[wei][mod][pos] != -1) return f[wei][mod][pos];
if (!wei && !mod && !pos) return 1;
if (!wei) return 0;
int maxn;
if (lim) maxn = n / power[wei - 1] % 10;
else maxn = 9;
int ans = 0;
for (int i = 0; i <= maxn; ++i) {
int t = (mod + 13 - i * power[wei - 1] % 13) % 13;
if (pos == 2) {
ans += dp(wei - 1, t, 2, lim & (i == maxn));
if (i == 1) ans += dp(wei - 1, t, 1, lim & (i == maxn));
}
if (pos == 1 && i == 3) ans += dp(wei - 1, t, 1, lim & (i == maxn)) + dp(wei - 1, t, 0, lim & (i == maxn));
if (pos == 0) {
if (i != 3) ans += dp(wei - 1, t, 0, lim & (i == maxn));
if (i != 3 && i != 1) ans += dp(wei - 1, t, 1, lim & (i == maxn));
}
}
if (lim) return ans;
else return f[wei][mod][pos] = ans;
}
int work(int x) {
if (x == 0) return 0;
int wei = 0;
while (x) {
x /= 10;
++wei;
}
return dp(wei, 0, 2, 1);
}
int main() {
init();
while (~scanf("%d", &n)) {
// cin >> n;
memset(f, -1, sizeof f );
f[0][0][0] = 1;
printf("%d\n", work(n));
}
return 0;
}
B.区间圆数
本来的思路就是像上一道题一样 搜 \(0\) 出现的次数
然后判次数是否超过总位数的一半
然后忘了前导 \(0\) 会有影响 直接寄掉了。。。
实际上这题另外记录一下前导 \(0\) 即可
另外事实上还是记录 \(0\) \(1\) 的次数更为合理
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 31;
int f[N][N][N], l, r;
int s[N];
int dp(int wei, int sum0, int sum1, bool lead, bool lim) {
if (wei == 0) {
if (lead || sum0 >= sum1) return 1;
else return 0;
}
if (!lead && !lim && f[wei][sum0][sum1] != -1) return f[wei][sum0][sum1];
int ans = 0;
int maxn;
if (lim) maxn = s[wei];
else maxn = 1;
for (int i = 0; i <= maxn; ++i) {
if (lead && i == 0) ans += dp(wei - 1, 0, 0, 1, lim & (i == maxn));
else {
if (i == 1) ans += dp(wei - 1, sum0, sum1 + 1, 0, lim & (i == maxn));
else ans += dp(wei - 1, sum0 + 1, sum1, 0, lim & (i == maxn));
}
}
// cout << wei << " " << sum0 << " " << sum1 << " " << lead << " " << lim << " " << ans << "\n";
if (!lead && !lim) return f[wei][sum0][sum1] = ans;
else return ans;
}
int work(int x) {
memset(f, -1, sizeof f);
int wei = 0;
while (x) {
s[++wei] = (x & 1);
x >>= 1;
}
return dp(wei, 0, 0, 1, 1);
}
int main() {
scanf("%d%d", &l, &r);
printf("%d",work(r) - work(l - 1));
return 0;
}
C.数字计数
对于此题 我们很容易发现 比如在 \(1-1000\) 和 \(1000-2000\) 中 算上前导 \(0\) 的话只看后三位所有数字出现的次数是一样的
我们尝试算出这个次数
首先 在 \(0-9\) 中 每个数字都出现了 \(1\) 次 这很显然
我们考虑 \(0-99\) \(0-9\) 在这里面出现了 \(10\) 遍 加上每个数作为十位数的时候 都出现了 \(10\) 遍 所以每个数出现了 \(10 + 10 = 20\) 次
再考虑 \(0-999\) 首先在这里面 \(0-99\) 出现了 \(10\) 遍 加上每个数作为百位数的时候 都出现了 \(100\) 遍 所以每个数共出现了 \(10 * 20 + 100 = 300\) 次
然后我们就有这样的式子 \(f[i] = f[i - 1] * 10 + power[i - 1]\)
我们再思考怎么算这个题
假如说这个数是 \(ABCD\) 我们考虑之前试填法或者 \(lim\) 的思想
当这位没满的时候 后面就随便填 当这位满的时候 后面就有限制
那假如说我填到 \(A\) 这一位 那么 \(0 - A-1\) 后面的数就都没有限制
那么就一共出现了 \(A * f[i - 1]\) 次 并且千位数每个都出现了 \(1000\) 次
然后对于最高位是 \(A\) 后面就有限制 递归下去即可 此时千位的 \(A\) 出现了 \(BCD\) 次
然后再减去前导 \(0\) 的个数 这题就解决了
代码写的非记搜
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 31;
ll f[N], power[N];
int s[N];
ll cnta[10], cntb[10], cnt[10];
ll a, b;
void init() {
power[0] = 1;
for (int i = 1; i <= 15; ++i) power[i] = 10 * power[i - 1];
for (int i = 1; i <= 15; ++i) f[i] = f[i - 1] * 10 + power[i - 1];
for (int i = 1; i <= 15; ++i) cout << f[i] << " ";
}
void solve(ll x) {
memset(cnt, 0, sizeof cnt);
int wei = 0;
ll tmp = x;
while (tmp) {
s[++wei] = tmp % 10;
tmp /= 10;
}
for (int i = wei; i; --i) {
for (int j = 0; j <= 9; ++j) cnt[j] += s[i] * f[i - 1];
for (int j = 0; j < s[i]; ++j) cnt[j] += power[i - 1];
cnt[s[i]] += x % power[i- 1] + 1;
cnt[0] -= power[i - 1];
}
}
int main() {
init();
scanf("%lld%lld", &a, &b);
solve(a - 1);
for (int i = 0; i <= 9; ++i) cnta[i] = cnt[i];
solve(b);
for (int i = 0; i <= 9; ++i) cntb[i] = cnt[i];
for (int i = 0; i <= 9; ++i) printf("%lld ",cntb[i] - cnta[i]);
return 0;
}
D.数字整除
首先算 \(\left[l, r\right]\) 区间可以转化为前缀和相减
然后显然要记录个位之和和整个数的大小
但是发现整个数的大小太大了 没法记录状态
想到对整个数用各位之和取模
但是会发现一个问题 各位之和只有搜到头才知道是多少 那我怎么在过程中随时取模呢
然后发现各位之和的范围很小 可以暴力枚举这个模数
然后搜到底的时候判断各位之和和枚举的这个模数是否相等即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll f[101][11][101][101];
int s[10];
int mod, l, r;
ll dp(int mod, int wei, int sum, int shu, bool lim) {
if (wei == 0) return sum == mod && shu == 0;
if (!lim && f[mod][wei][sum][shu] != -1) return f[mod][wei][sum][shu];
int maxn = lim? s[wei]: 9;
ll ans = 0;
for (int i = 0; i <= maxn; ++i) {
ans += dp(mod, wei - 1, sum + i, (shu * 10 + i) % mod, lim & (i == maxn));
}
if (!lim) return f[mod][wei][sum][shu] = ans;
else return ans;
}
ll solve(int x) {
int wei = 0;
while (x) {
s[++wei] = x % 10;
x /= 10;
}
ll ret = 0;
for (mod = 1; mod <= 9 * wei; ++mod) ret += dp(mod, wei, 0, 0, 1);
return ret;
}
int main() {
memset(f, -1, sizeof f);
while (~scanf("%d%d", &l, &r)) {
printf("%lld\n", solve(r) - solve(l - 1));
}
return 0;
}
E.山谷数
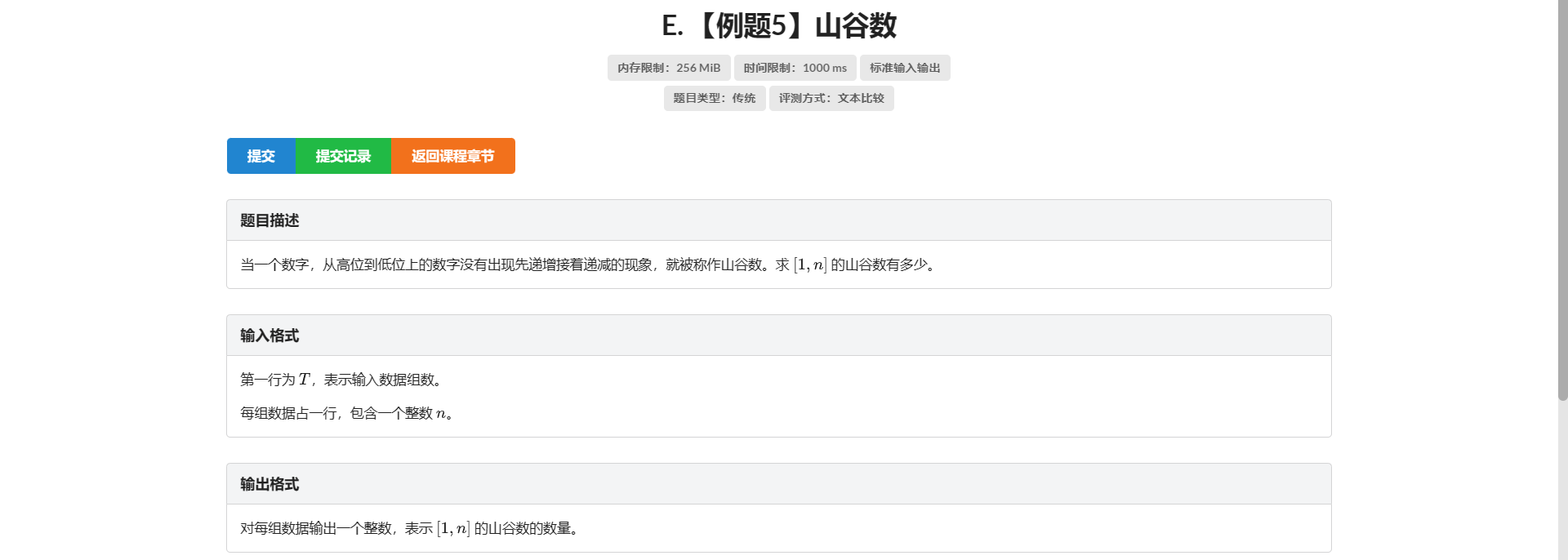
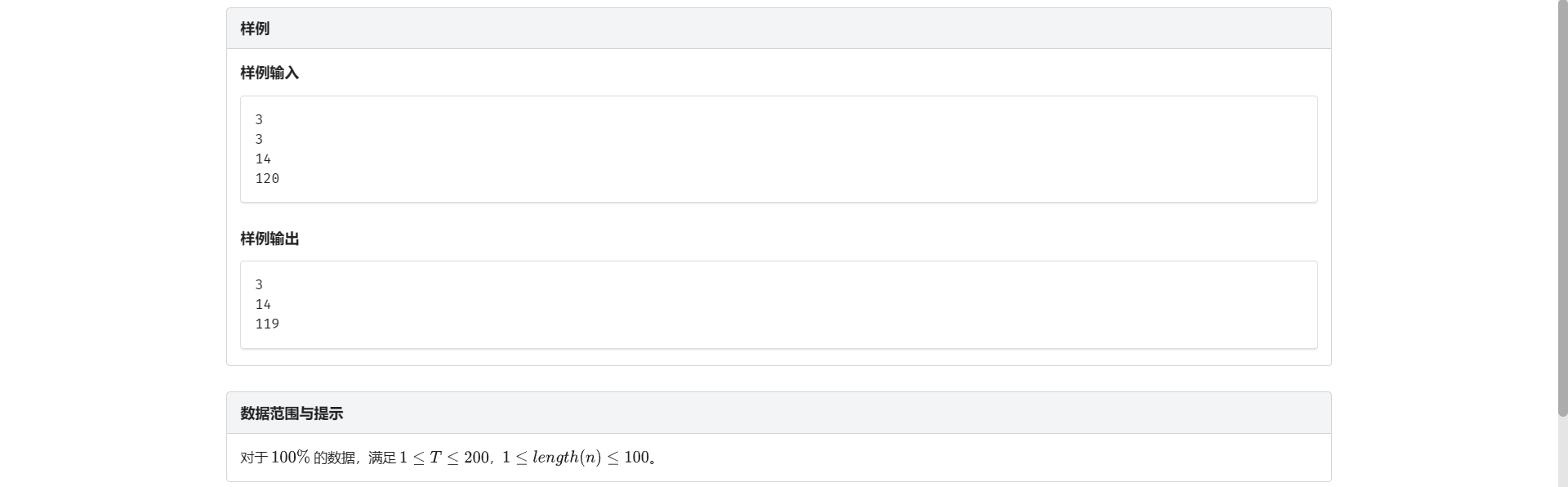
首先这题要对 \(10^9 + 7\) 取模 题面没说
然后我们要记录当前递增/递减/不变的状况
又因为要记录当前变化 所以还要记录上一个数是啥
再然后还要判前导 \(0\)
然后就没有然后了
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 1e9 + 7;
ll f[101][11][3];
string s;
int n[101];
int T;
ll dp(int wei, int pre, int k, bool lead, bool lim) {
if (wei == 0) return !lead;
if (!lead && !lim && f[wei][pre][k] != -1) return f[wei][pre][k];
int maxn = lim? n[wei]: 9;
ll ans = 0;
for (int i = 0; i <= maxn; ++i) {
if (k == 1 && i < pre) continue;
if (lead) ans = (ans + dp(wei - 1, i, k, lead & (i == 0), lim & (i == maxn))) % mod;
else if (i == pre) ans = (ans + dp(wei - 1, i, k, 0, lim & (i == maxn))) % mod;
else ans = (ans + dp(wei - 1, i, (i < pre ? 2: 1), 0, lim & (i == maxn))) % mod;
}
if (!lim && !lead) return f[wei][pre][k] = ans;
else return ans;
}
ll solve() {
memset(f, -1, sizeof f);
int wei = s.length();
for (int i = 1, j = wei - 1; i <= wei; ++i, --j) n[i] = s[j] - '0';
return dp(wei, 0, 0, 1, 1);
}
int main() {
scanf("%d", &T);
while (T--) {
cin >> s;
printf("%lld\n",solve());
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号