YBTOJ 5.2区间DP
A.石子合并
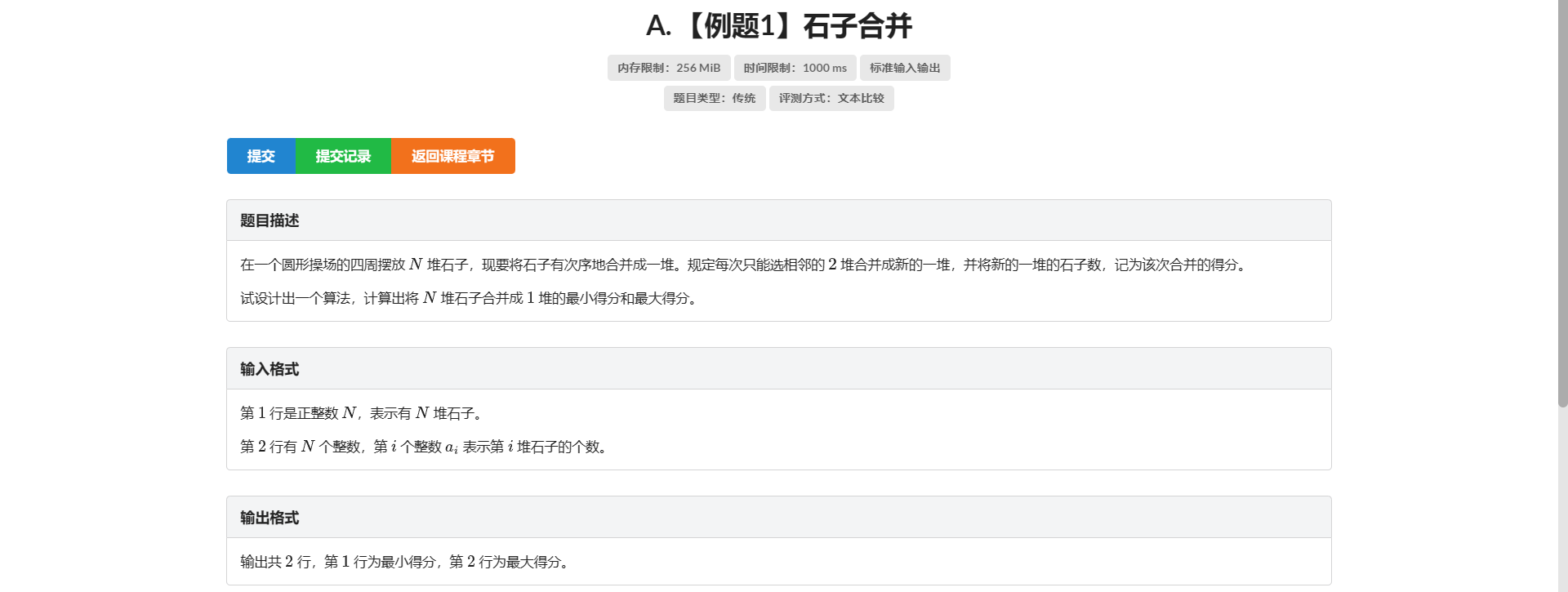
很经典的区间 \(DP\) 模板题
我们设 \(f[l][r]\) 表示把 \(\left[l, r\right]\) 这段区间的最小/大得分
考虑枚举 \(\left[l, r\right]\) 之间的断点 \(k\) 有 \(f[l][r] = max/min(f[l][k] + f[k][r])\)
但是由于这题是要考虑 我们考虑把原队列复制一份放在末尾
然后枚举一个长度为 \(n\) 的定区间
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 201;
int a[N], dpmax[N][N], dpmin[N][N];
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) a[i + n] = a[i];
for (int len = 2; len <= n; len++) {
for (int i = 1; i <= 2 * n + 1 - len; i++) {
dpmin[i][i + len - 1] = 0x7fffffff;
for (int k = 0; k < len - 1; k++) {
dpmax[i][i + len - 1] =
max(dpmax[i][i + k] + dpmax[i + k + 1][i + len - 1], dpmax[i][i + len - 1]);
dpmin[i][i + len - 1] =
min(dpmin[i][i + k] + dpmin[i + k + 1][i + len - 1], dpmin[i][i + len - 1]);
}
for (int k = i; k <= i + len - 1; k++) {
dpmax[i][i + len - 1] += a[k];
dpmin[i][i + len - 1] += a[k];
}
}
}
int maxn = 0, minn = 0x7fffffff;
for (int i = 1; i <= 2 * n + 1 - n; i++) {
maxn = max(maxn, dpmax[i][i + n - 1]);
minn = min(minn, dpmin[i][i + n - 1]);
}
printf("%d\n%d", minn, maxn);
return 0;
}
B.木板涂色
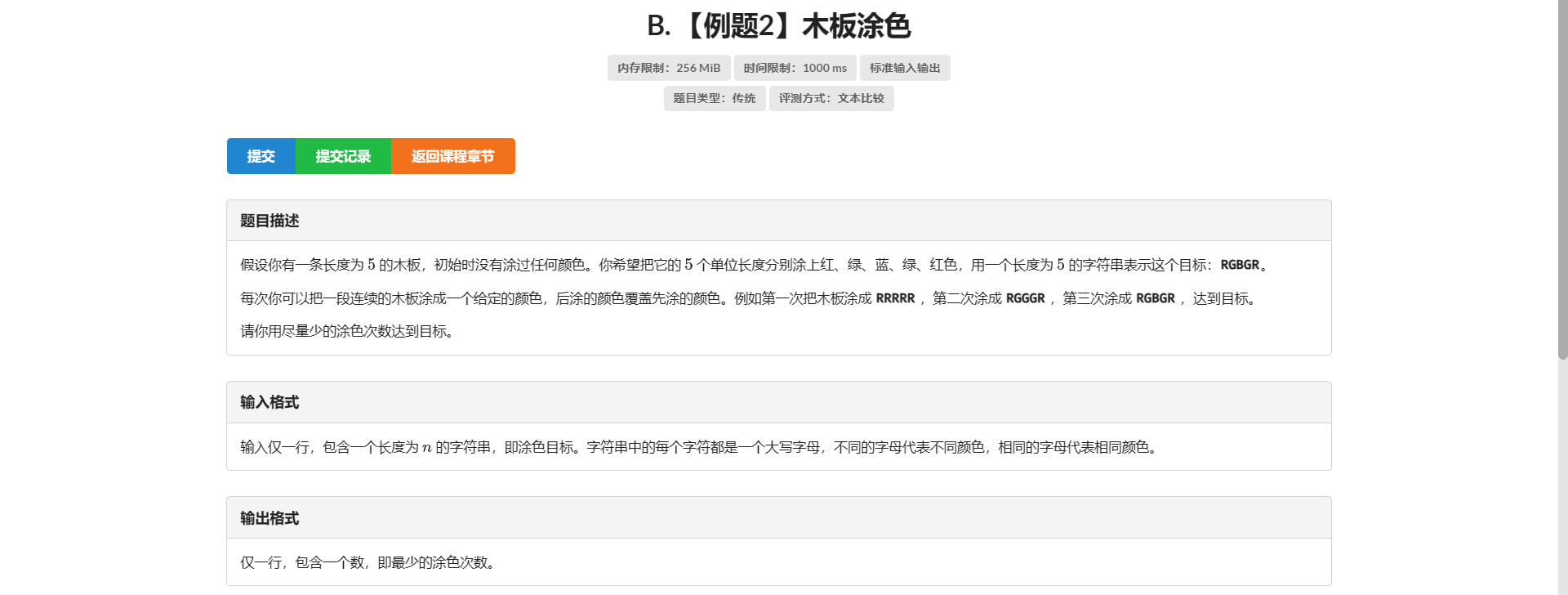
因为数据范围比较美丽 并且涂色是一个区间的操作
所以可以考虑一下区间 \(DP\)
设 \(f[l][r]\) 表示把 \(\left[l, r\right]\) 刷到目标状态的最小次数花费
考虑转移 还是有 \(f[l][r] = min(f[l][k] + f[k][r])\)
但问题在于 题目给的颜色没用上
发现如果 \(l\) 和 \(r\) 颜色相同 只需要刷一次
所以有 \(f[l][r] = min(f[l + 1][r], f[l][r - 1])\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 52;
int f[N][N];
string s;
int main() {
cin >> s;
int n = s.length();
memset(f, 0x3f, sizeof f );
for (int i = 0; i < n; ++i) f[i][i] = 1;
for (int len = 2; len <= n; ++len) {
for (int l = 0; l + len - 1 < n; ++l) {
int r = l + len - 1;
if (s[l] == s[r])
f[l][r] = min(f[l][r - 1], f[l + 1][r]);
else {
for (int k = l; k < r; ++k)
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r]);
}
}
}
printf("%d",f[0][n - 1]);
return 0;
}
C.消除木块
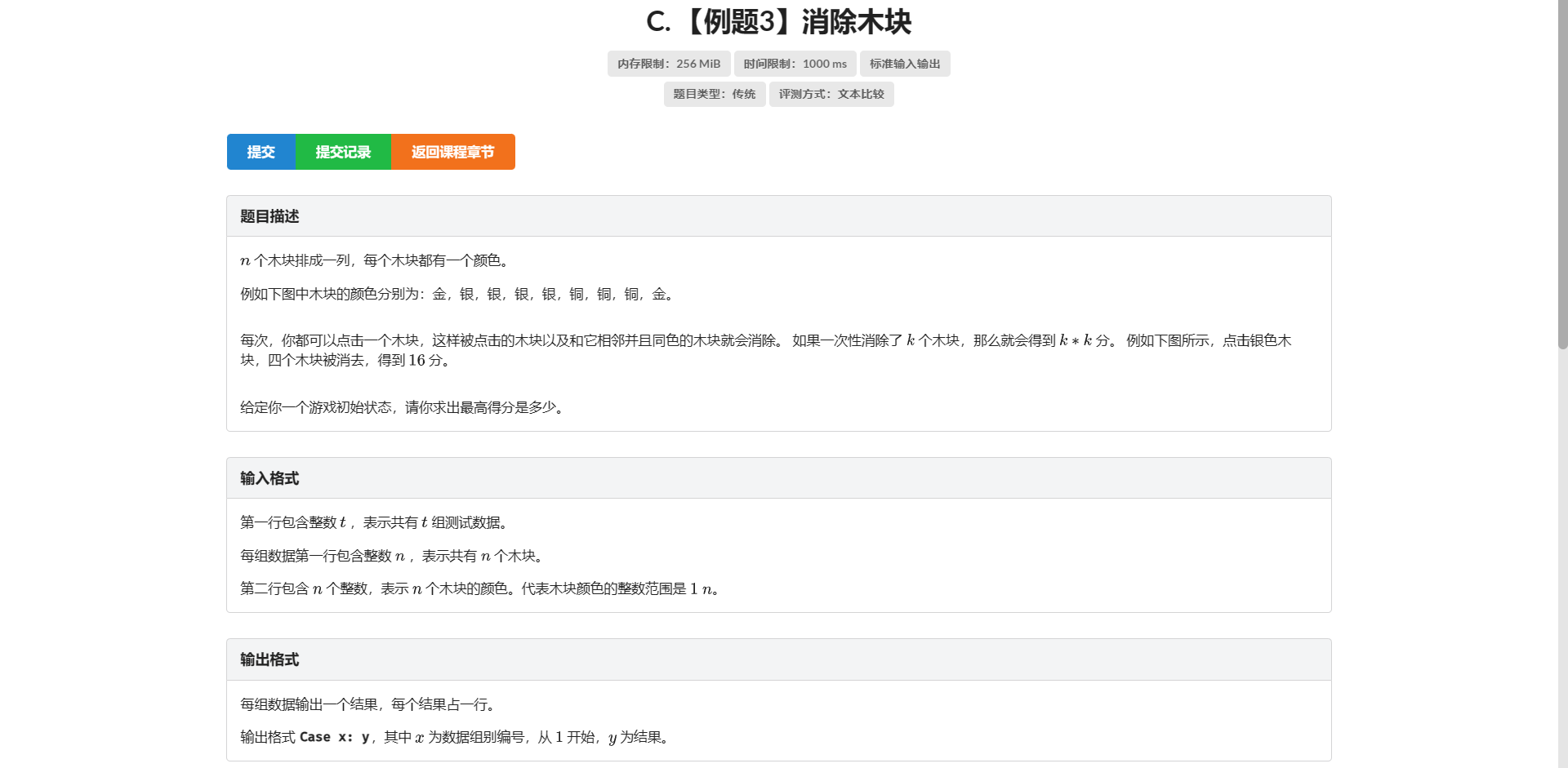
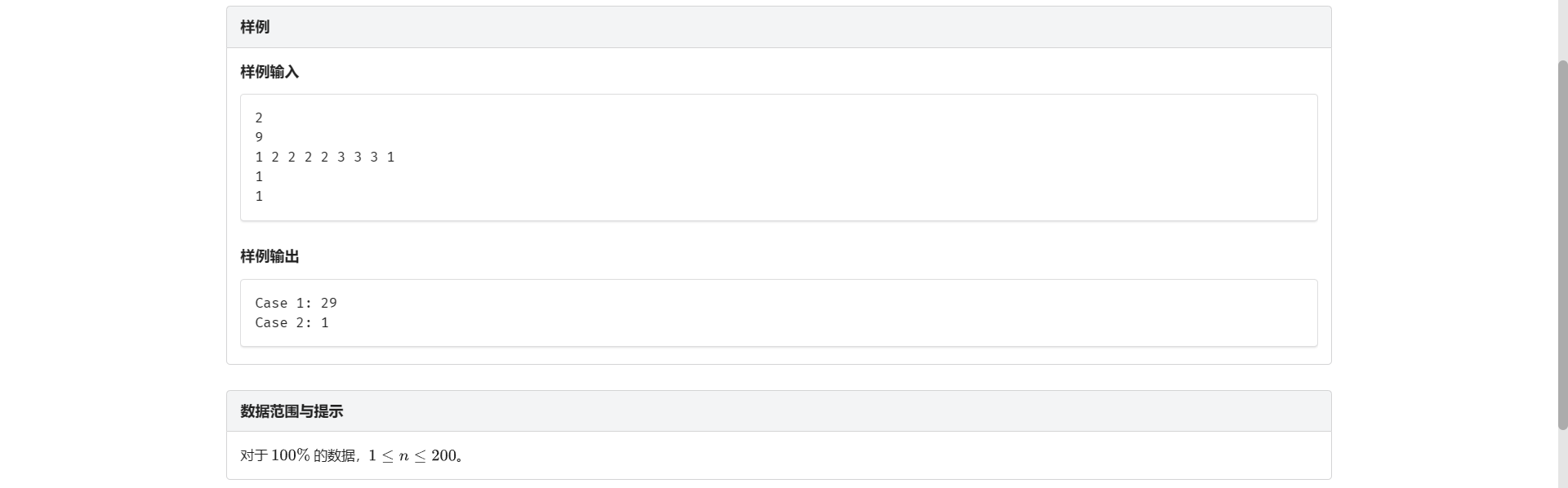
头疼
考虑区间 \(DP\) 设 \(f[l][r]\) 表示把 \(\left[l, r\right]\) 区间内所有木块都消除的最大得分
但是转移不太好想 单纯枚举 \(k\) 的话还是那个问题:颜色是干什么用的
并且假如说我把 \(r\) 单独炸掉 那如果 \(r\) 后面还有相同颜色的拼在一起 显然就不合法了
那么我们考虑设 \(f[l][r][x]\) 表示连接 \(r\) 后面还有多少同色木块
那么显然有一个决策是直接把 \(r\) 和它连着的那一段全炸掉
或者考虑枚举 \(\left[l, r\right]\) 之间的 \(k\)
但是要有一些特点 比如说...与 \(r\) 颜色相同?
那我们把 \(\left[k + 1, r - 1\right]\) 这段崩掉
那 \(r\) 和 \(k\) 就拼在一起了
具体转移可以使用记搜:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 301;
int f[N][N][N];
int co[N], len[N], a[N];
int T, n;
int jyhss(int l, int r, int k) {
int all = len[r] + k;
if (l == r) return all * all;
if (f[l][r][k] != -1) return f[l][r][k];
int res = jyhss(l, r - 1, 0) + all * all;
for (int kkk = l; kkk < r; ++kkk) {
if (co[kkk] == co[r])
res = max(res, jyhss(l, kkk, all) + jyhss(kkk + 1, r - 1, 0));
}
return f[l][r][k] = res;
}
int main() {
scanf("%d", &T);
for (int ii = 1; ii <= T; ++ii) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
int lst = -1, cnt = 0;
for (int i = 1; i <= n; ++i) {
if (lst != a[i]) {
++cnt;
len[cnt] = 1;
co[cnt] = a[i];
lst = a[i];
} else ++len[cnt];
}
// for (int i = 1; i <= cnt; ++i) cout<<i<<" "<<co[i]<<" "<<len[i]<<endl;
memset(f, -1, sizeof f );
printf("Case %d: %d\n",ii,jyhss(1, cnt, 0));
}
return 0;
}
D.棋盘分割
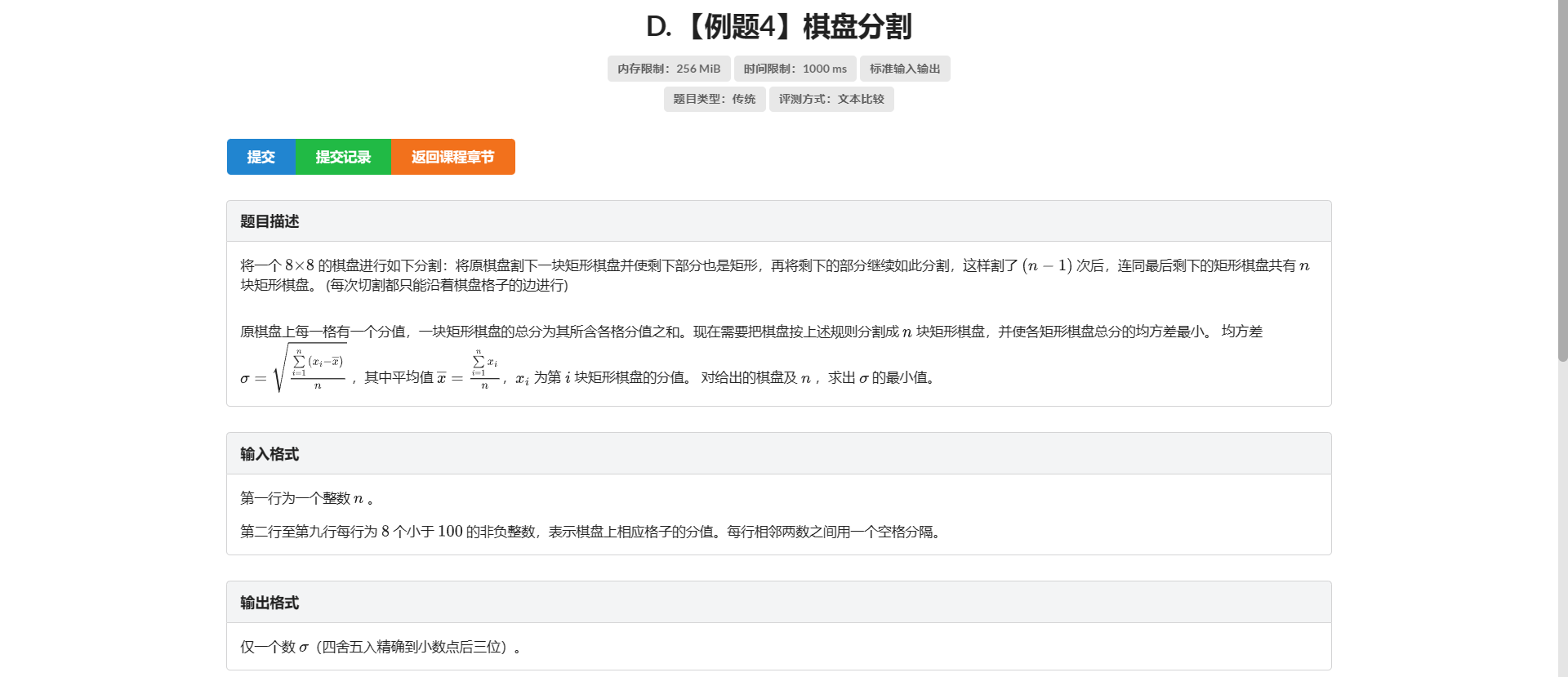
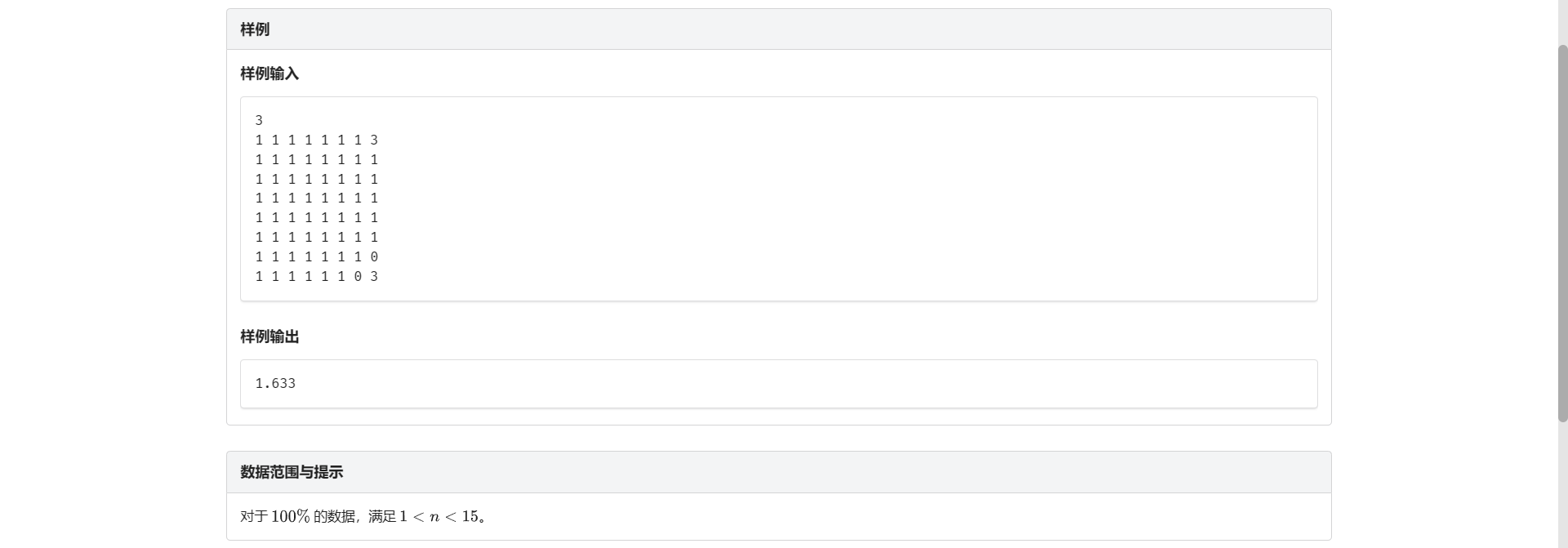
二维区间 \(DP\)
式子看起来很吓人 但是考虑转化一下
首先根号是无所谓的 我们让根号里的东西尽可能大就行
除以 \(n\) 当然也是无所谓的 因为 \(n\) 是定值
进一步观察 发现 \(\bar{x}\) 也是无所谓的 因为它等于全图中所有数的和除以 \(n\)
而上面打开就是 \(\sum\limits_{i=1}^n x_i^2 + \bar{x}^2 - 2 * \bar{x} * x_i\)
它等于 \(n * \bar{x}^2 - 2 * \bar{x} * \sum\limits_{i=1}^n x_i + \sum\limits_{i=1}^n x_i^2\)
其中 \(\sum\limits_{i=1}^n x_i\) 显然还是全图中所有数的和
所以我们就求 \(\sum\limits_{i=1}^n x_i^2\) 的最大值
考虑区间 \(DP\) 设 \(f[x_1][y_1][x_2][y_2][k]\) 表示左上角为 \((x_1, y_1)\) 右下角为 \((x_2, y_2)\) 大小的矩形被切了 \(k\) 刀的 \(\sum\limits_{i=1}^n x_i^2\)
然后枚举切的那刀的位置即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int a[10][10];
int f[10][10][10][10][N];
int n;
double avr;
int count(int x1, int y1, int x2, int y2) {
int sum = 0;
for (int i = x1; i <= x2; ++i) {
for (int j = y1; j <= y2; ++j) sum += a[i][j];
}
return sum * sum;
}
void getavr(void) {
int sum = 0;
for (int i = 1; i <= 8; ++i) {
for (int j = 1; j <= 8; ++j) sum += a[i][j];
}
avr = (double)sum / (n + 1);
}
int main() {
scanf("%d", &n);
--n;
for (int i = 1; i <= 8; ++i) {
for (int j = 1; j <= 8; ++j) scanf("%d", &a[i][j]);
}
getavr();
memset(f, 0x3f, sizeof f );
for (int lx = 1; lx <= 8; ++lx) {
for (int x1 = 1; x1 + lx - 1 <= 8; ++x1) {
int x2 = x1 + lx - 1;
for (int ly = 1; ly <= 8; ++ly) {
for (int y1 = 1; y1 + ly - 1 <= 8; ++y1) {
int y2 = y1 + ly - 1;
f[x1][y1][x2][y2][0] = count(x1, y1, x2, y2);
}
}
}
}
for (int i = 1; i <= n; ++i) {
for (int lx = 1; lx <= 8; ++lx) {
for (int x1 = 1; x1 + lx - 1 <= 8; ++x1) {
int x2 = x1 + lx - 1;
for (int ly = 1; ly <= 8; ++ly) {
for (int y1 = 1; y1 + ly - 1 <= 8; ++y1) {
int y2 = y1 + ly - 1;
for (int kx = x1; kx < x2; ++kx) {
f[x1][y1][x2][y2][i] = min( f[x1][y1][x2][y2][i], f[x1][y1][kx][y2][0] + f[kx + 1][y1][x2][y2][i - 1]);
f[x1][y1][x2][y2][i] = min( f[x1][y1][x2][y2][i], f[x1][y1][kx][y2][i - 1] + f[kx + 1][y1][x2][y2][0]);
}
for (int ky = y1; ky < y2; ++ky) {
f[x1][y1][x2][y2][i] = min(f[x1][y1][x2][y2][i], f[x1][y1][x2][ky][0] + f[x1][ky + 1][x2][y2][i - 1]);
f[x1][y1][x2][y2][i] = min(f[x1][y1][x2][y2][i], f[x1][y1][x2][ky][i - 1] + f[x1][ky + 1][x2][y2][0]);
}
}
}
}
}
}
double ans = (double)f[1][1][8][8][n];
ans = ans / (n + 1);
printf("%.3lf",sqrt(ans - avr * avr));
return 0;
}
E.删数问题
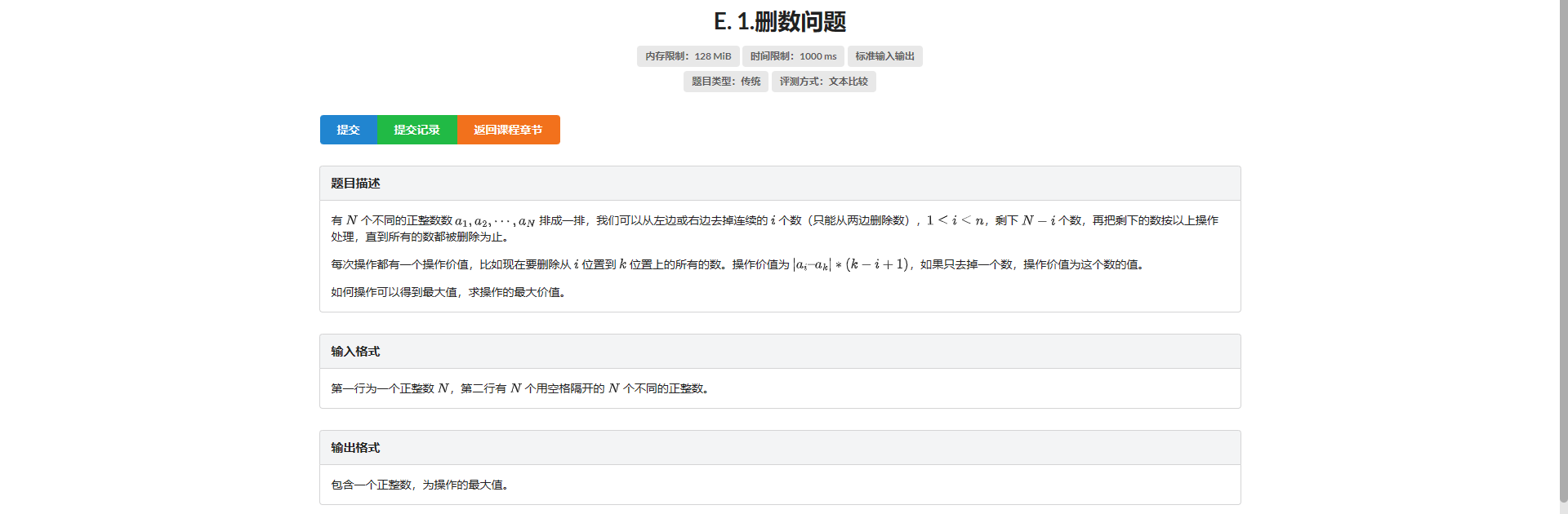
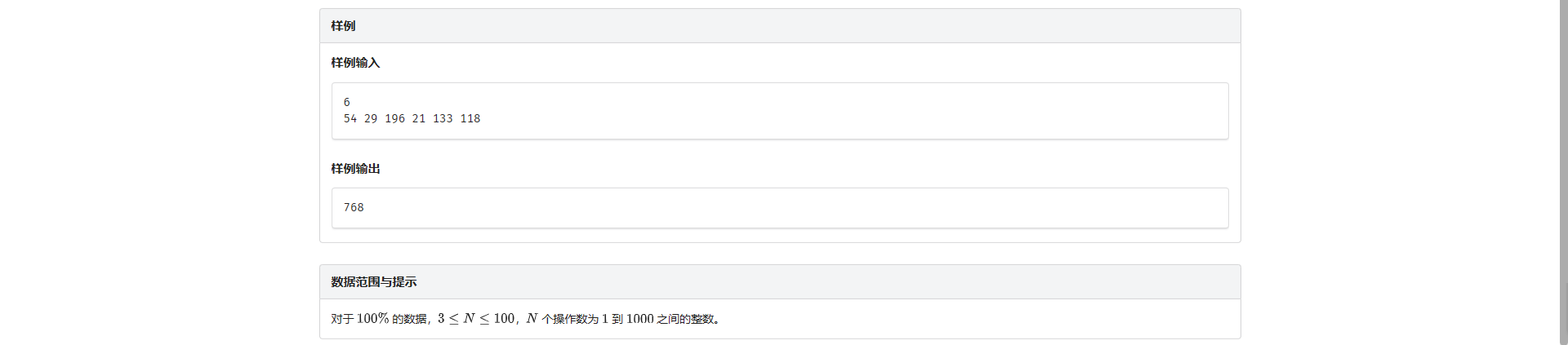
设 \(f_{l, r}\) 表示把 \(\left[l, r\right]\) 这段区间的数全删掉的最大收益
那我们就有两种选择:
- 一次操作把整个区间都删掉
- 枚举断点 \(k\) 拆成 \(f_{l, k} + f_{k + 1, r}\)
然后直接转移即可
- 为什么这样操作一定是合法的
考虑最后构成答案的操作一定为 \(\left[x_1, x_2\right], \left[x_2, x_3\right], ..., \left[x_{s - 1}, x_s\right]\) 这若干个连续区间
那么我们按顺序删 一定可以保证删除操作合法
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 105;
int a[N];
ll f[N][N];
int n;
ll calc(int l, int r) {
if (l == r) return 1ll * a[l];
else return 1ll * abs(a[l] - a[r]) * (r - l + 1);
}
void main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) f[i][i] = a[i];
for (int len = 2; len <= n; ++len) {
for (int l = 1; l + len - 1 <= n; ++l) {
int r = l + len - 1;
f[l][r] = calc(l, r);
for (int k = l; k < r; ++k) f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r]);
}
}
printf("%lld\n", f[1][n]);
}
}
int main() {
steven24::main();
return 0;
}
/*
6
54 29 196 21 133 118
*/
F.恐狼后卫
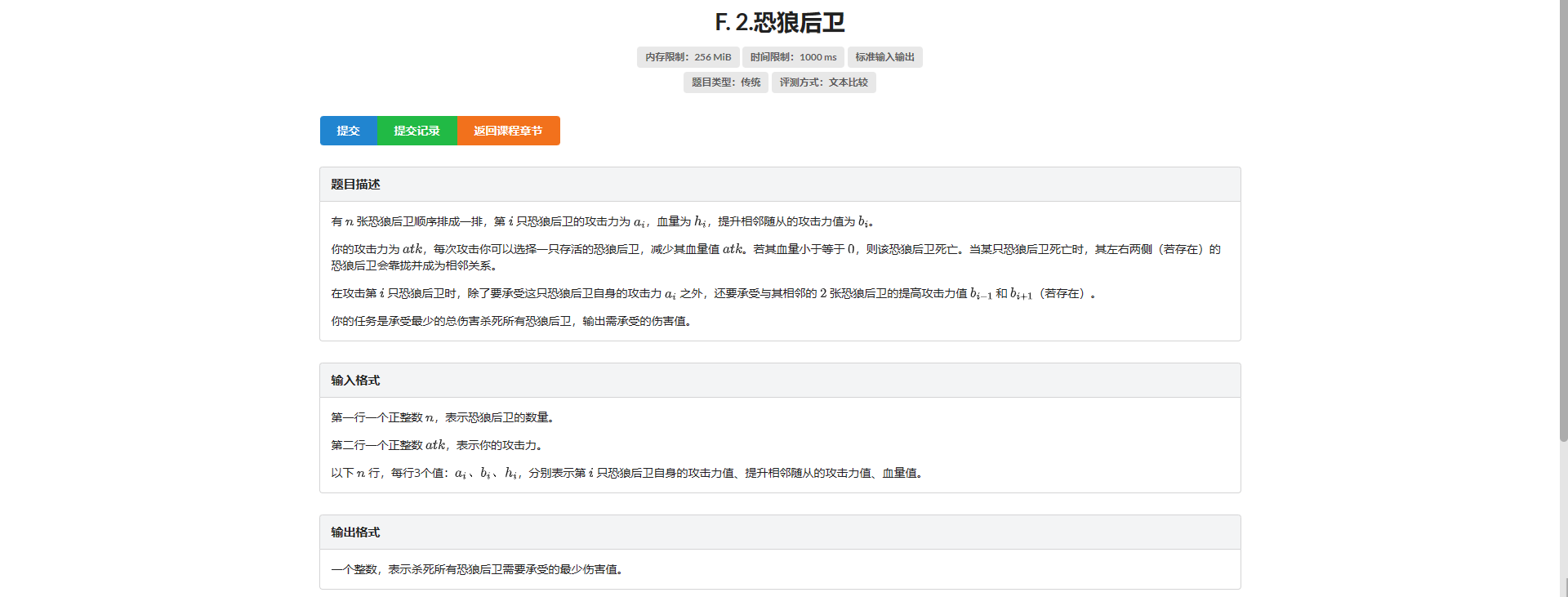
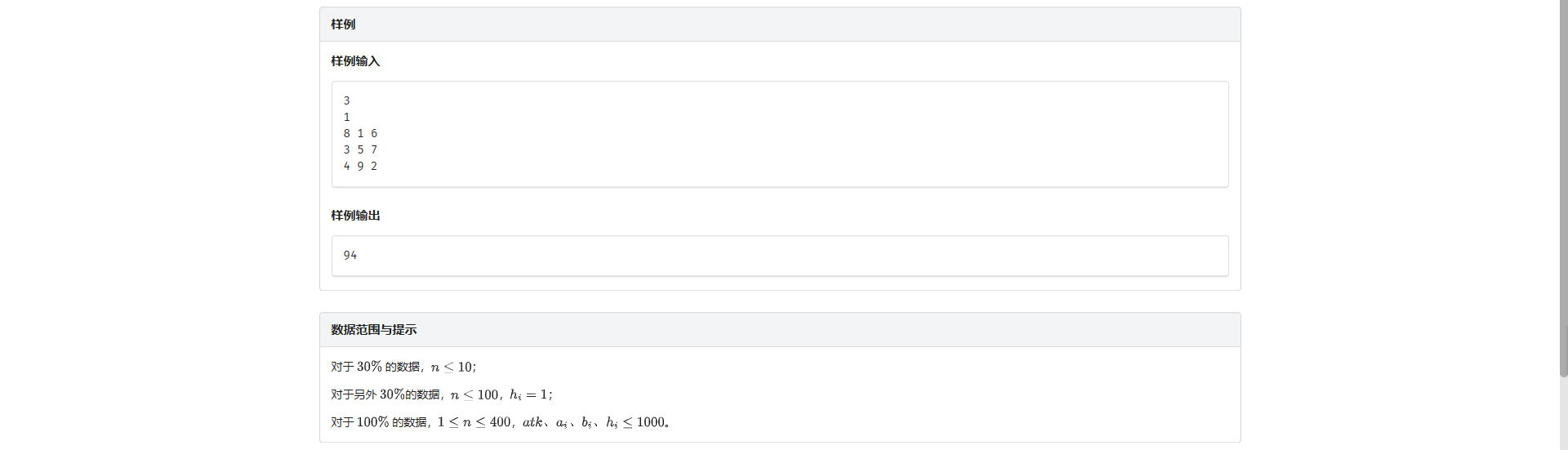
有个比较直觉的想法:如果要对一只狼开刀 最好的选择一定是直接砍到死
考虑证明
首先我们要对一只狼砍的刀数是一定的 也就是说我们承受伤害的次数是一定的
并且该狼的攻击力一定 所以有影响的一定是它左右两只狼
假设我承受 \(b_{x_1}, b_{y_1}\) 的攻击力砍了若干刀 \(b_{x_2}, b_{y_2}\) 的攻击力砍了若干刀...等等直到把它砍死
那么也就说明我可以通过一些方式使任何 \((x_i, y_i)\) 都取的到
那么我们选取其中代价最小的一组 把这只狼直接从满血砍到死 一定是小于等于上述操作的代价的
然后考虑如何区间 DP
设 \(f_{l, r}\) 表示把 \(\left[l + 1, r - 1\right]\) 的狼全砍死需要的最小代价
转移的时候枚举断点 \(k\) 把 \(k\) 从满血砍到死
那么我们就要先把 \(\left[l + 1, k - 1\right]\) 和 \(\left[k + 1, r - 1\right]\) 这两个区间的狼全砍死
然后承受 \(b_l, b_r\) 的代价
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 520;
const ll inf = 0x7ffffffffffffff;
ll f[N][N];
int a[N], b[N], hp[N];
int n, atk;
int get(int x) {
if (x < atk) return 1;
int ret = x / atk;
if (x % atk != 0) ++ret;
return ret;
}
int main() {
scanf("%d%d", &n, &atk);
for (int i = 1; i <= n; ++i) scanf("%d%d%d", &a[i], &b[i], &hp[i]);
for (int len = 3; len <= n + 2; ++len) {
for (int l = 0; l + len - 1 <= n + 1; ++l) {
int r = l + len - 1;
f[l][r] = inf;
for (int k = l + 1; k <= r - 1; ++k) f[l][r] = min(f[l][r], f[l][k] + get(hp[k]) * (a[k] + b[l] + b[r]) + f[k][r]);
}
}
printf("%lld",f[0][n + 1]);
return 0;
}
G.矩阵取数
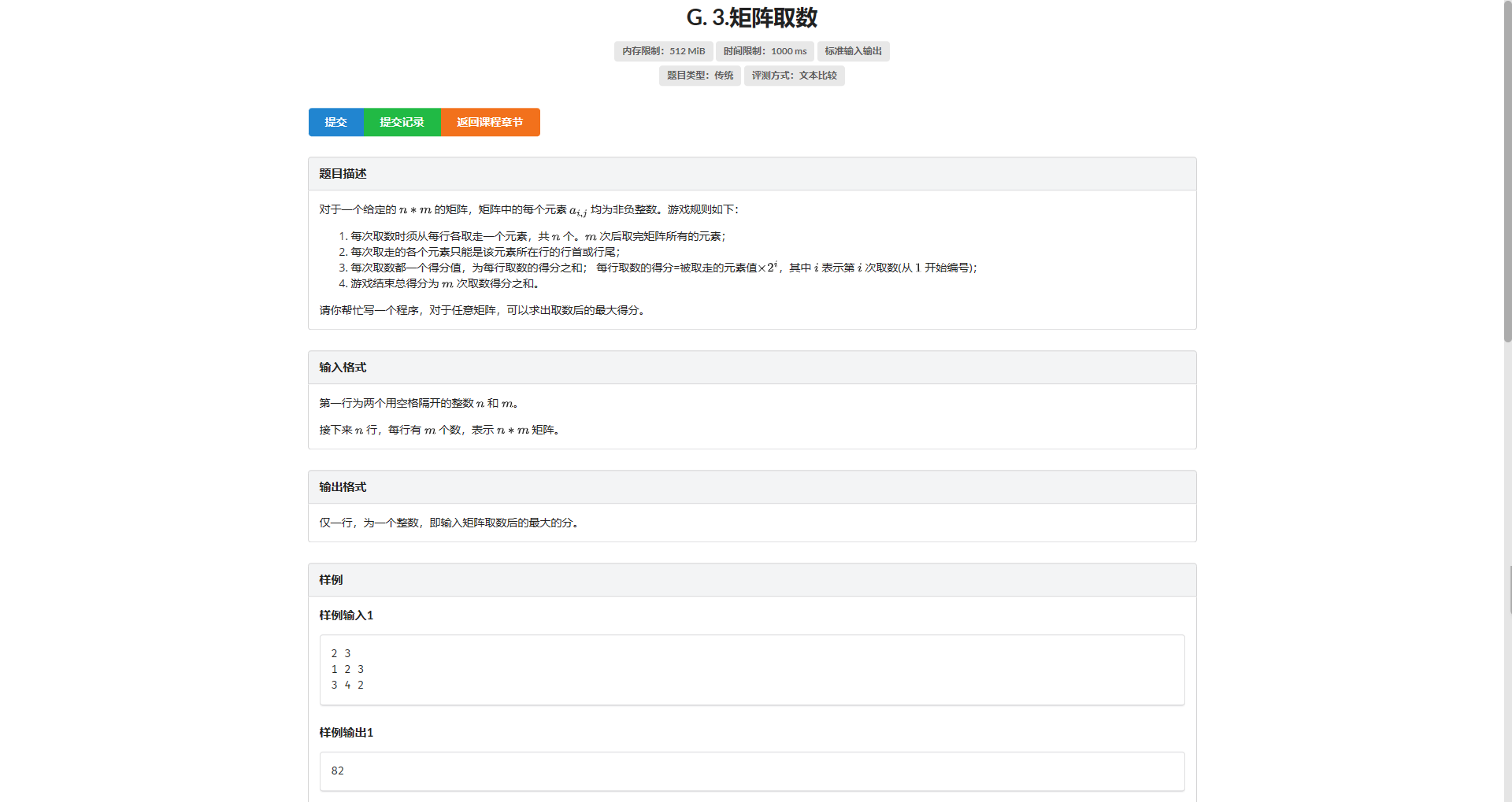
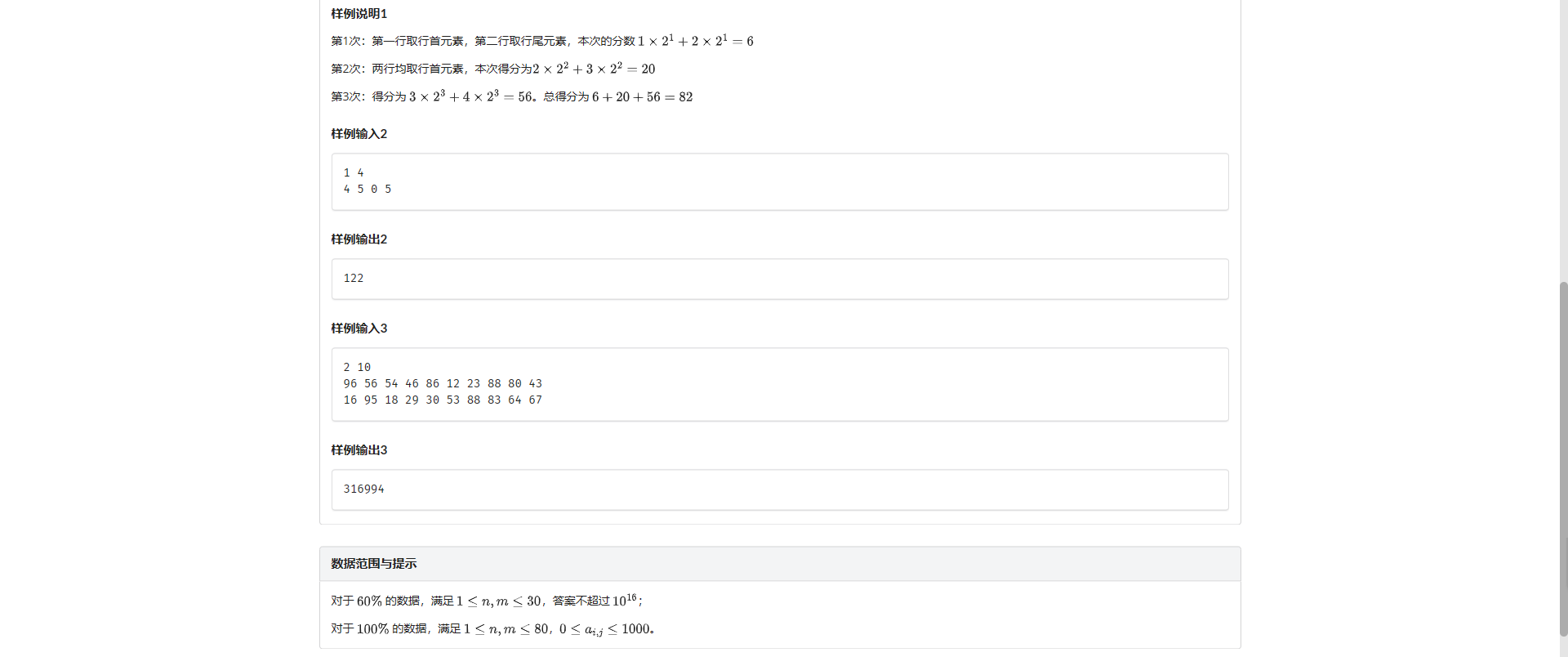
观察发现每一行之间相互不影响 所以我们可以每一行都分别做一次 然后累加答案
设 \(f_{l, r}\) 表示 \(\left[l, r\right]\) 这段区间的得分 那么显然有 \(f_{l, r} = \max(f_{l + 1, r} + cost_l, f_{l, r - 1} + cost_r)\)
那么问题的关键就是求出当前拿走这个数的得分
进一步观察可以发现 因为是 \(m\) 次取完 所以如果区间长度已知那么当前操作是第几次取数是一定的
稍微推一下:
总长为 \(m\)
区间长为 \(m\) :第一次取数
区间长为 \(m - 1\) :第二次取数
区间长为 \(1\) :第 \(m\) 次取数
区间长为 \(len\) :第 \(m - len + 1\) 次取数
答案要开高精 偷懒直接 __int128 也行
点击查看代码
#include <bits/stdc++.h>
#define int __int128
using namespace std;
namespace steven24 {
int f[101][101];
int base[101];
int a[101][101];
int n, m;
int ans;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void write(int x) {
if (x < 0) putchar('-'), x = -x;
if (x >= 10) write(x / 10);
putchar(x % 10 + '0');
}
void init() {
base[0] = 1;
for (int i = 1; i <= m; ++i) base[i] = base[i - 1] * 2;
}
void main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) a[i][j] = read();
}
init();
for (int s = 1; s <= n; ++s) {
for (int i = 1; i <= m; ++i) f[i][i] = base[m] * a[s][i];
for (int len = 2; len <= m; ++len) {
for (int l = 1; l + len - 1 <= m; ++l) {
int r = l + len - 1;
f[l][r] = max(f[l + 1][r] + a[s][l] * base[m - len + 1], f[l][r - 1] + a[s][r] * base[m - len + 1]);
// write(l), putchar(' '), write(r), putchar(' '), write(f[l][r]), putchar('\n');
}
}
ans += f[1][m];
}
write(ans);
}
}
signed main() {
steven24::main();
return 0;
}
/*
2 3
1 2 3
3 4 2
*/
H.生日欢唱
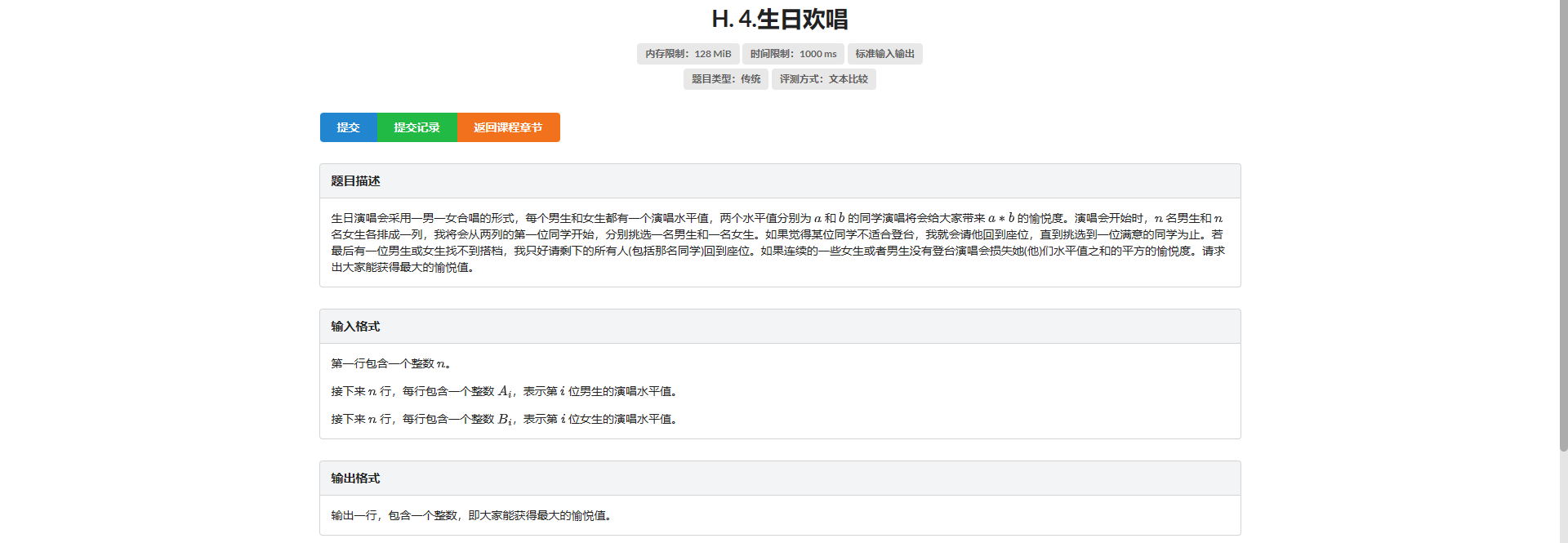
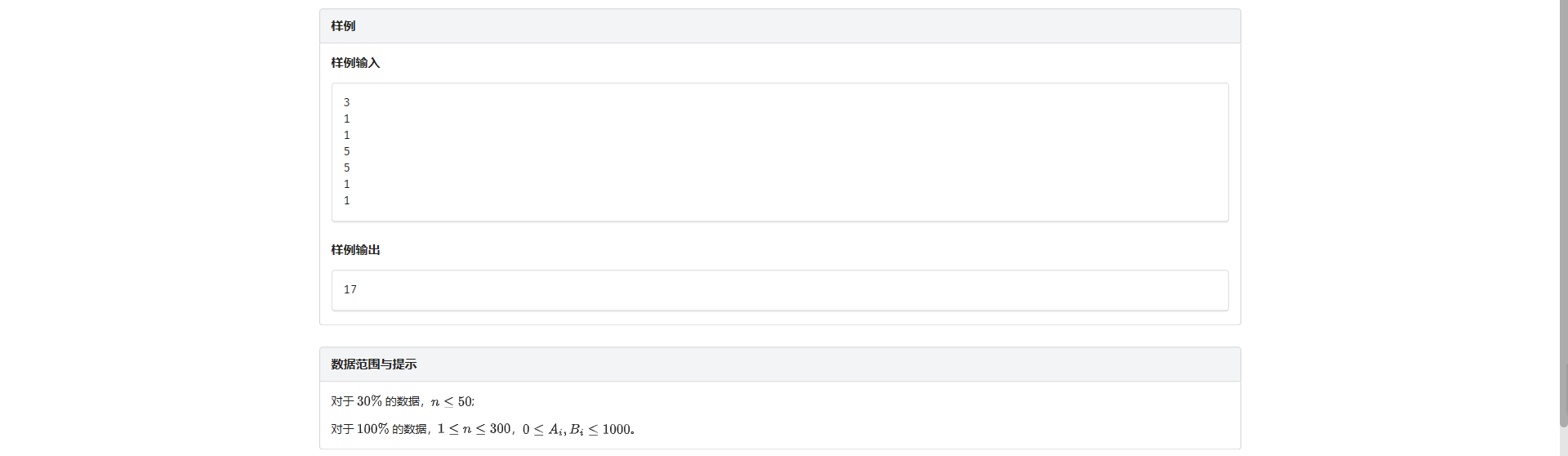
其实感觉不太像区间 DP
设 \(f_{l,r}\) 表示强制使男生第 \(l\) 个和女生第 \(r\) 个配对的最大价值
枚举 \(l, r\) 前面的 \(i, j\) 则有 \(f_{l, r} = f_{i, j} - cost_{i + 1 , l - 1} - cost_{j + 1, r - 1} + val_{l, r}\)
其中 \(cost_{l, r}\) 表示把 \(\left[l, r\right]\) 这段区间的学生全删掉的代价
但是这样转移是 \(\text{O}(n ^ 4)\) 的
通过进一步思考性质 我们可以发现 如果两个前面都丢掉了人 一定是亏的
所以直接枚举 \(l\) 这边丢掉多少人和 \(r\) 这边丢掉多少人即可
查询代价需要加个前缀和预处理
这样就是 \(\text{O}(n ^ 3)\) 了
对于答案 我们直接在每个 \(f_{l, r}\) 转移出来之后 算出把剩下学生都丢掉的代价减掉 然后与答案取 \(\max\) 即可
注意初值问题
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 521;
ll f[N][N];
int a[2][N];
int d[2][N];
int n;
ll ans;
void init() {
for (int j = 0; j <= 1; ++j) {
for (int i = 1; i <= n; ++i) d[j][i] = d[j][i - 1] + a[j][i];
}
}
ll calc(int l, int r, int opt) {
if (l > r) return 0;
int sum = d[opt][r] - d[opt][l - 1];
return 1ll * sum * sum;
}
void main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[0][i]);
for (int i = 1; i <= n; ++i) scanf("%d", &a[1][i]);
init();
memset(f, -0x3f, sizeof f);
f[0][0] = 0;
for (int l = 1; l <= n; ++l) {
for (int r = 1; r <= n; ++r) {
for (int k = 0; k < l; ++k) f[l][r] = max(f[l][r], f[k][r - 1] - calc(k + 1, l - 1, 0) + 1ll * a[0][l] * a[1][r]);
for (int k = 0; k < r; ++k) f[l][r] = max(f[l][r], f[l - 1][k] - calc(k + 1, r - 1, 1) + 1ll * a[0][l] * a[1][r]);
ans = max(ans, f[l][r] - calc(l + 1, n, 0) - calc(r + 1, n, 1));
}
}
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
3
1 1 5
5 1 1
*/
I.最小代价
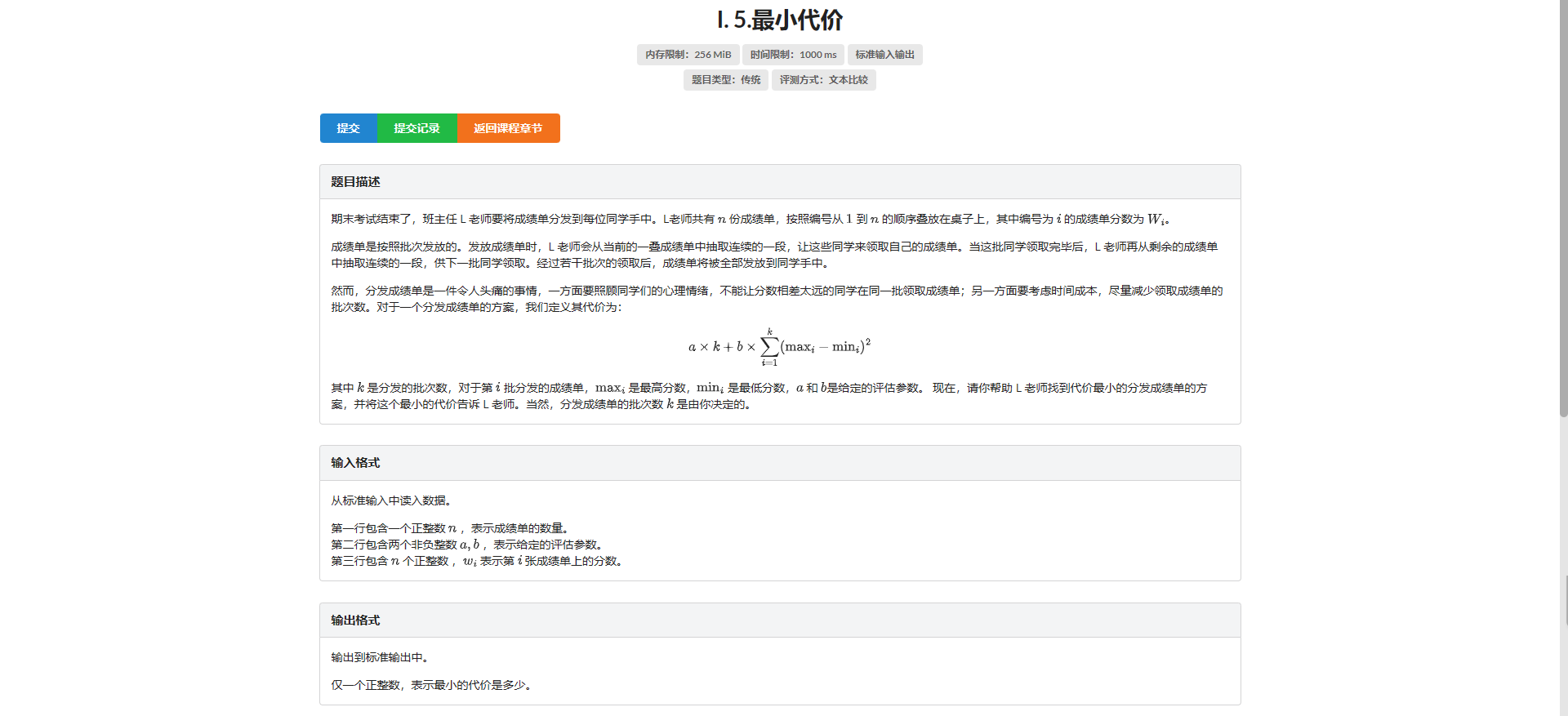
\(DAY^{-1}\)
设 \(dp_{l, r}\) 表示把 \(\left[l, r\right]\) 这段区间都消掉的代价
设 \(f_{l, r, x, y}\) 表示把 \(\left[l, r\right]\) 这段区间内除了值域在 \(\left[x, y\right]\) 的所有数都消掉的代价
那么显然有 \(dp_{l, r} = \min(f_{l, r, x, y} + A + B \times (y - x)^2)\)
然后我们考虑 \(f\) 数组的转移
考虑枚举断点 有
\(f_{l, r, x, y} = \min(dp_{l, k} + f_{k + 1, r, x, y})\)
\(f_{l, r, x, y} = \min(f_{l, k, x, y} + dp_{k + 1, r})\)
\(f_{l, r, x, y} = \min(f_{l, k, x, y} + f_{k + 1, r, x, y})\)
对于初值 有
\(dp_{i, i} = A\)
\(f_{i, i, 1 \text{~} a_i, a_i \text{~} maxn} = 0\)
结合上面的定义应该不难理解
此题需要离散化
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 52;
ll f[N][N][N][N], dp[N][N];
int a[N], b[N];
int n, A, B, tot;
ll ans = 0x7fffffff;
void discretization() {
memcpy(b, a, sizeof a);
sort(b + 1, b + 1 + n);
tot = unique(b + 1, b + 1 + n) - b - 1;
for (int i = 1; i <= n; ++i) a[i] = lower_bound(b + 1, b + 1 + tot, a[i]) - b;
}
void dfs(int l, int r) {
if (l > r) return;
if (dp[l][r] != 0x3f3f3f3f3f3f3f3f) return;
for (int x = 1; x <= tot; ++x) {
for (int y = x; y <= tot; ++y) {
for (int k = l; k < r; ++k) {
dfs(l, k);
dfs(k + 1, r);
f[l][r][x][y] = min(f[l][r][x][y], dp[l][k] + f[k + 1][r][x][y]);
f[l][r][x][y] = min(f[l][r][x][y], f[l][k][x][y] + dp[k + 1][r]);
f[l][r][x][y] = min(f[l][r][x][y], f[l][k][x][y] + f[k + 1][r][x][y]);
dp[l][r] = min(dp[l][r], f[l][r][x][y] + A + B * (b[y] - b[x]) * (b[y] - b[x]));
}
}
}
}
void main() {
scanf("%d%d%d", &n, &A, &B);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
discretization();
memset(dp, 0x3f, sizeof dp);
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; ++i) dp[i][i] = A;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= a[i]; ++j) {
for (int k = a[i]; k <= tot; ++k) f[i][i][j][k] = 0;
}
}
dfs(1, n);
printf("%lld\n", dp[1][n]);
}
}
int main() {
steven24::main();
return 0;
}
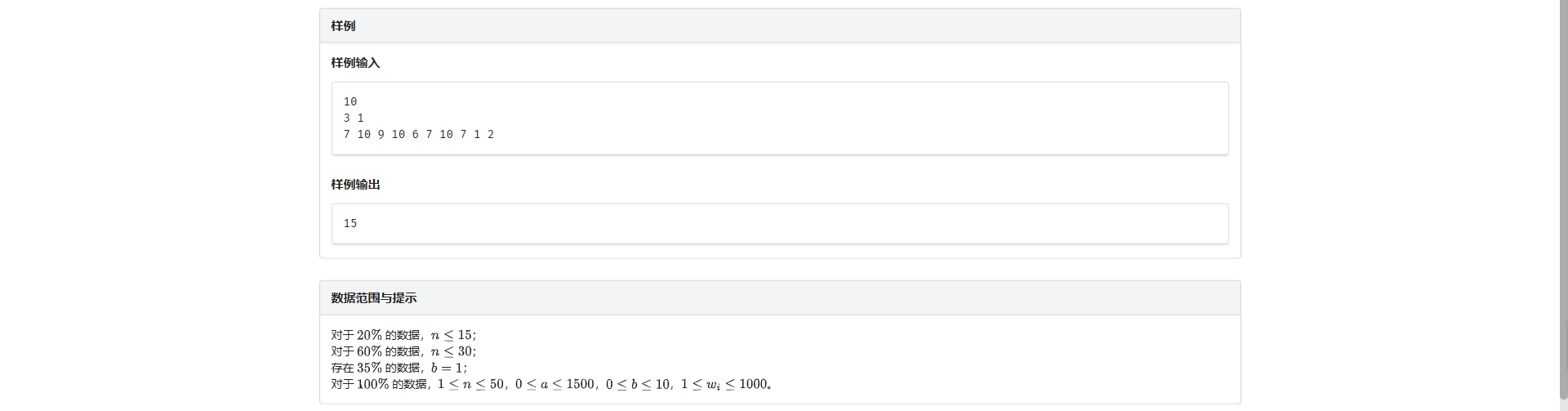
/*
10
3 1
7 10 9 10 6 7 10 7 1 2
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号