YBTOJ 5.1背包问题
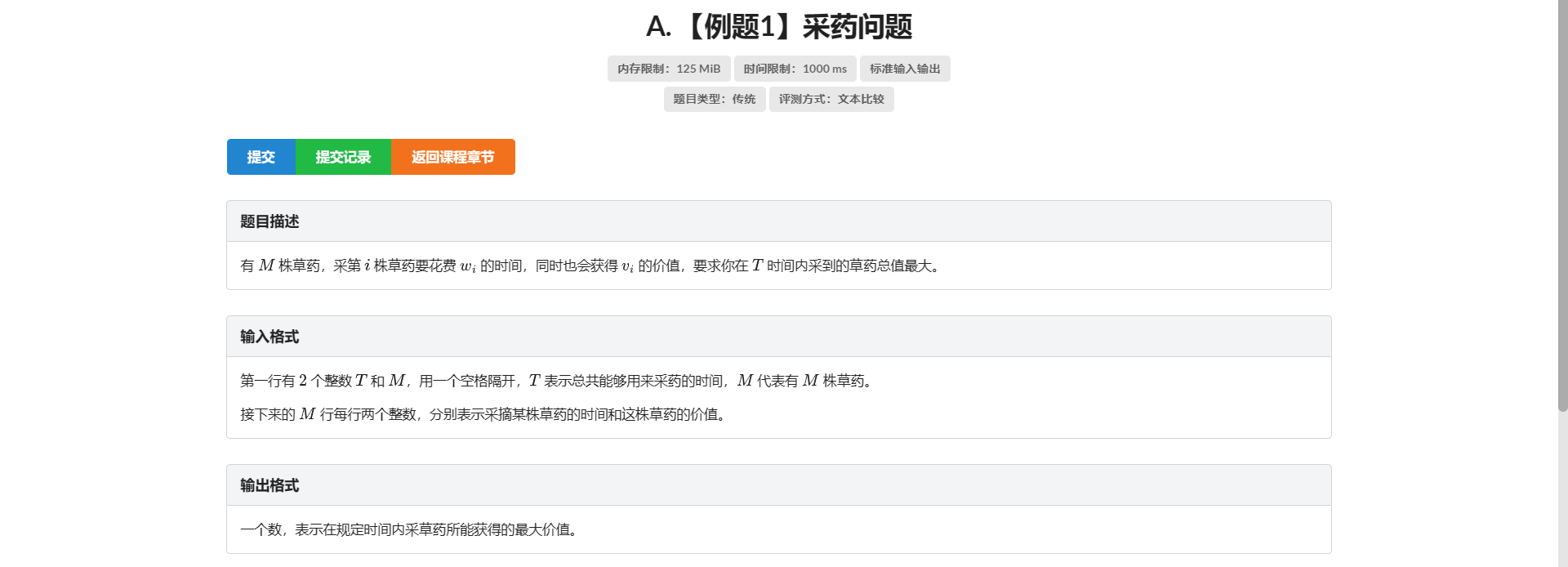
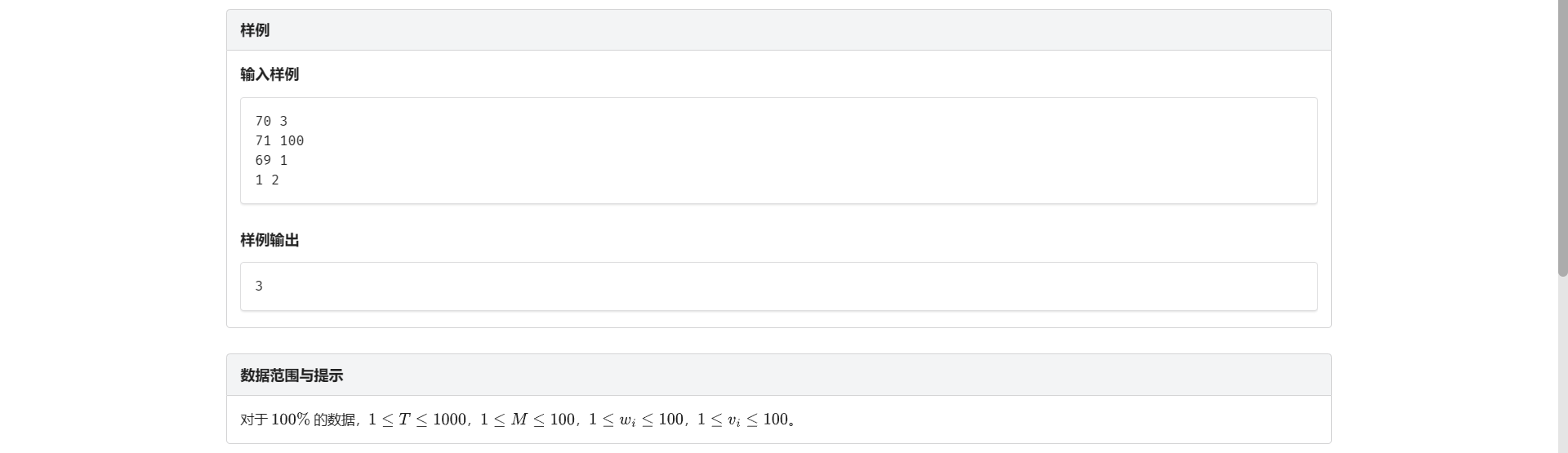
A.采药问题
\(01\) 背包板子题
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1001;
int w[N], c[N];
int mem[N][N];
int n, t;
int dfs(int x, int left) {
if (mem[x][left] != -1)
return mem[x][left];
if (x == n + 1) {
mem[x][left] = 0;
return 0;
}
int dfs1 = 0, dfs2 = 0;
dfs1 = dfs(x + 1, left);
if (left >= w[x])
dfs2 = dfs(x + 1, left - w[x]) + c[x];
mem[x][left] = max(dfs1, dfs2);
return mem[x][left];
}
int main() {
scanf("%d%d", &t, &n);
for (int i = 1; i <= n; ++i) scanf("%d%d", &w[i], &c[i]);
memset(mem, -1, sizeof(mem));
printf("%d", dfs(1, t));
return 0;
}
这好像是我练记搜的时候写的 无所谓了
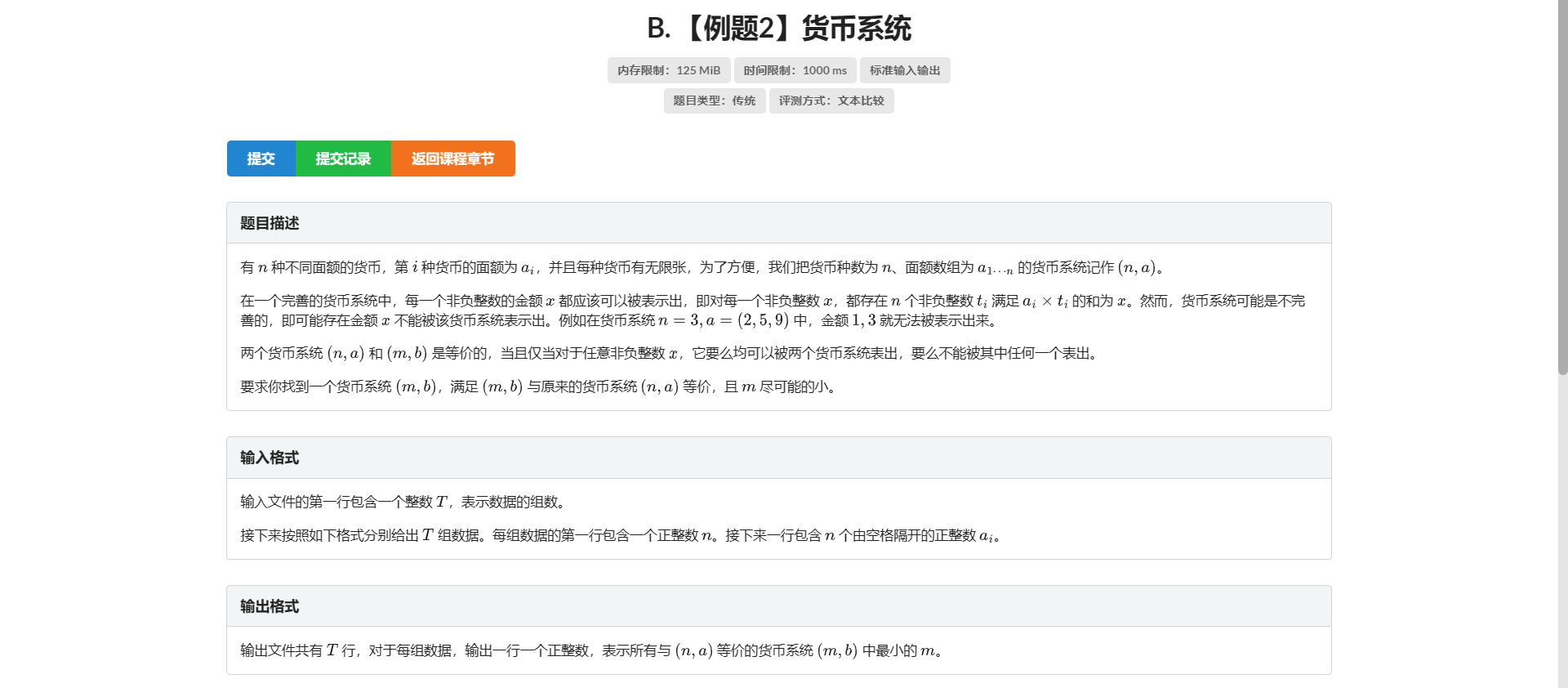
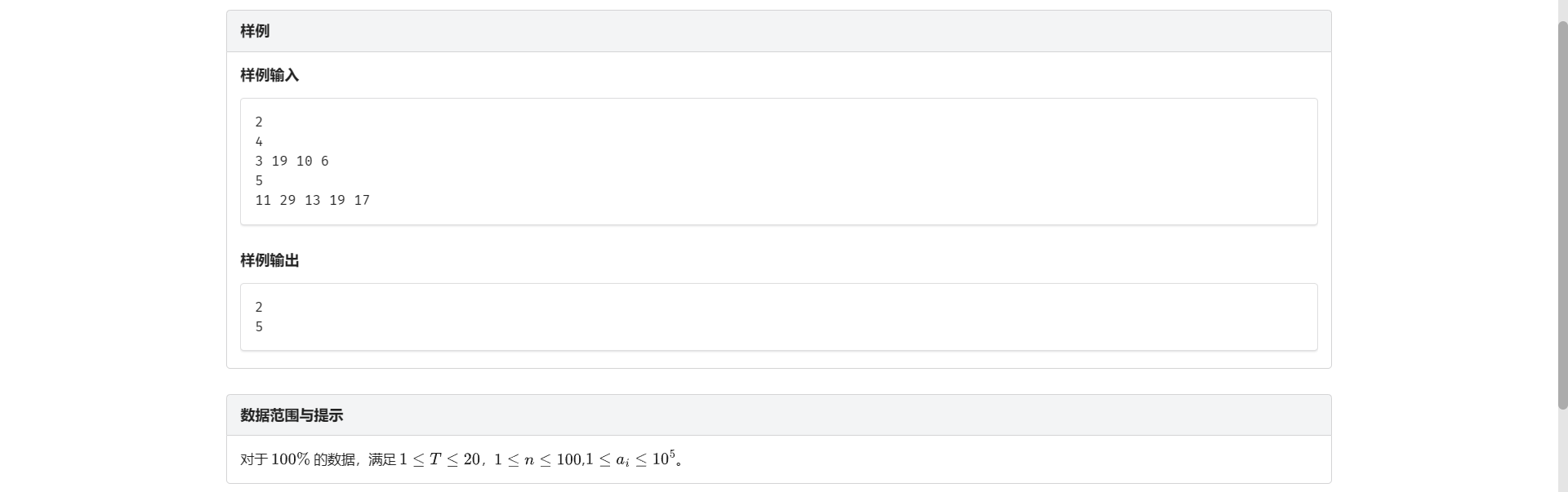
B.货币系统
经典做起来不难证起来很麻烦
非常直观的一个思路就是从所给的硬币集合中
踢掉可以由别的硬币就能表示出来的硬币
然后就过了
但是如果要严谨的话 肯定是需要证一下为什么不从所给集合外选
首先肯定不能选原来就表示不出来的 因为如果选了它就可以表示出来自己
其次如果选原来能表示出来的 假如说原来集合是 \(2 3 7\)
然后我选了个 \(5\)
那么如果我不选 \(2\) 或 \(3\) 显然表示不出来它们自己
如果我把这俩选出来了 那也没必要选 \(5\) 了
所以就从原集合中选
然后就是个完全背包了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 123;
int f[100721], a[N];
int n, T;
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
int ans = n;
memset(f, 0, sizeof f );
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
sort(a + 1, a + 1 + n);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
if (f[a[i]]) {
--ans;
continue;
}
for (int j = a[i]; j <= a[n]; ++j) {
if (f[j - a[i]])
f[j] = 1;
}
}
printf("%d\n",ans);
}
return 0;
}
C.宝物筛选
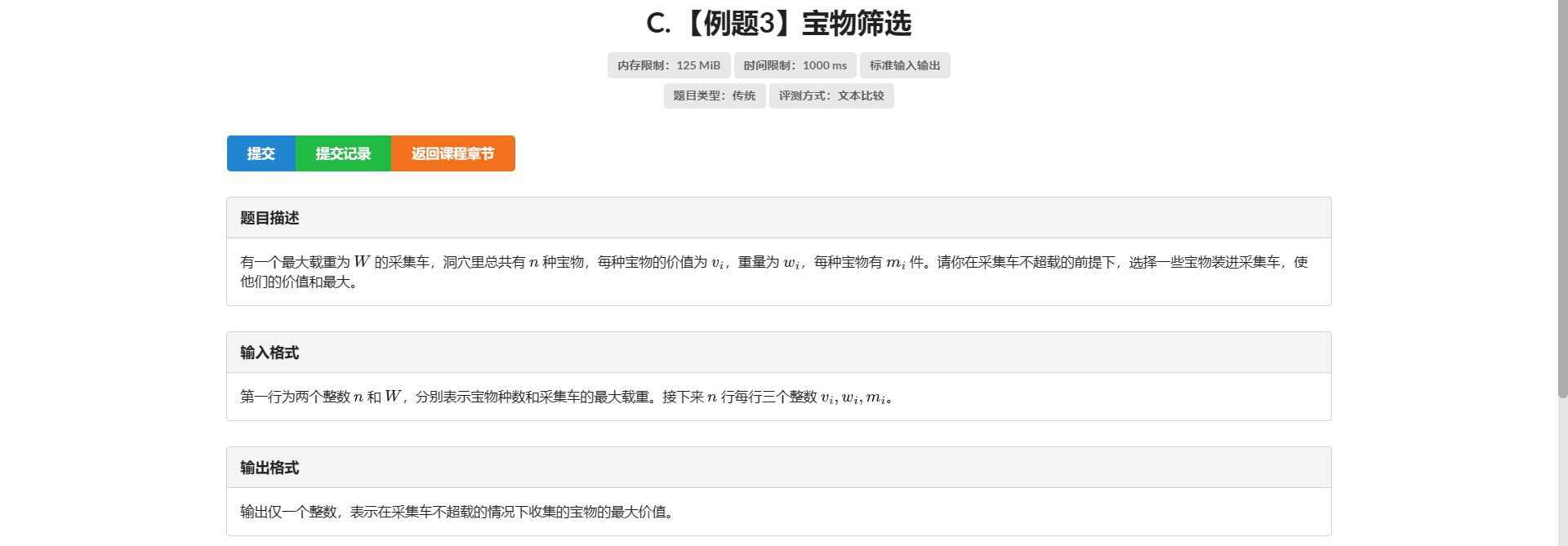
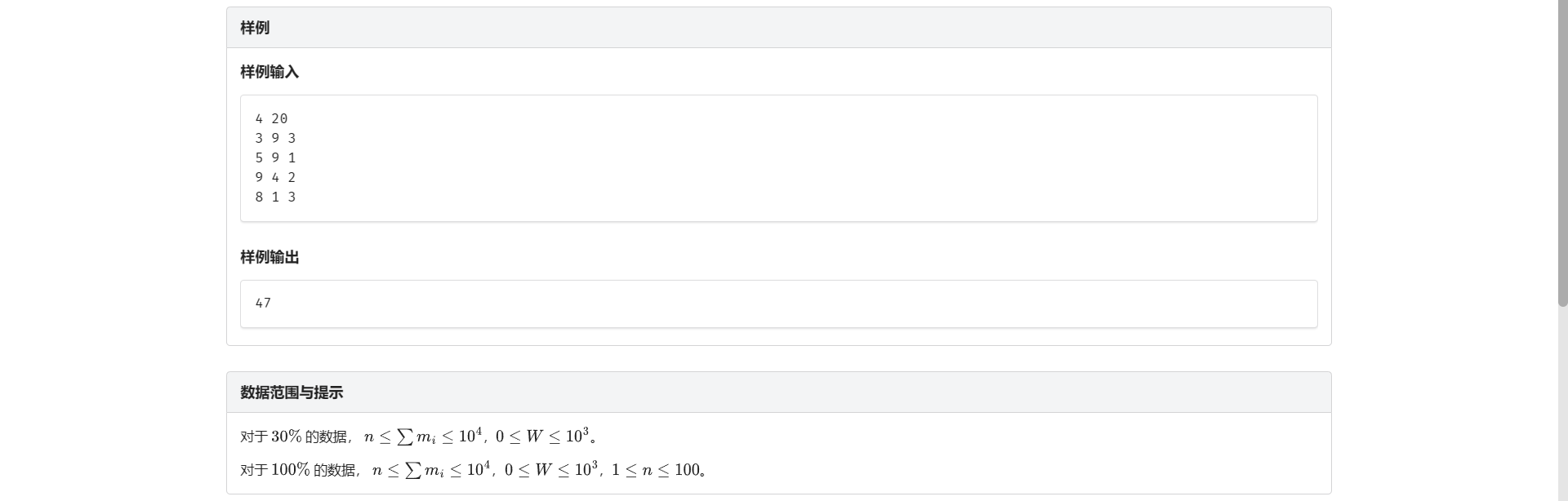
观前提示:主播不会二进制拆分
首先非常暴力的暴力就是 \(O(m * n * s)\)
考虑优化
因为我们转移的时候本来是要枚举 \(k\)
实际上转移区间就是 \(i - 1\) 那行 前面固定的 \(m + 1\) 个点
并且是求这一段定区间的最大值 想到可以用单调队列优化
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int f[40037], g[40037], q[40037];
int main() {
int n, W;
scanf("%d%d", &n, &W);
for (int i = 1; i <= n; i++) {
memcpy(g, f, sizeof(f));
int v, w, m;
scanf("%d%d%d", &v, &w, &m);
for (int j = 0; j < w; j++) {
int h = 0, t = -1;
for (int k = j; k <= W; k += w) {
if (h <= t && q[h] < k - m * w)
h++;
if (h <= t)
f[k] = max(g[k], g[q[h]] + (k - q[h]) / w * v);
while (h <= t && g[k] > g[q[t]] + (k - q[t]) / w * v) t--;
q[++t] = k;
}
}
}
printf("%d", f[W]);
return 0;
}
D.硬币方案
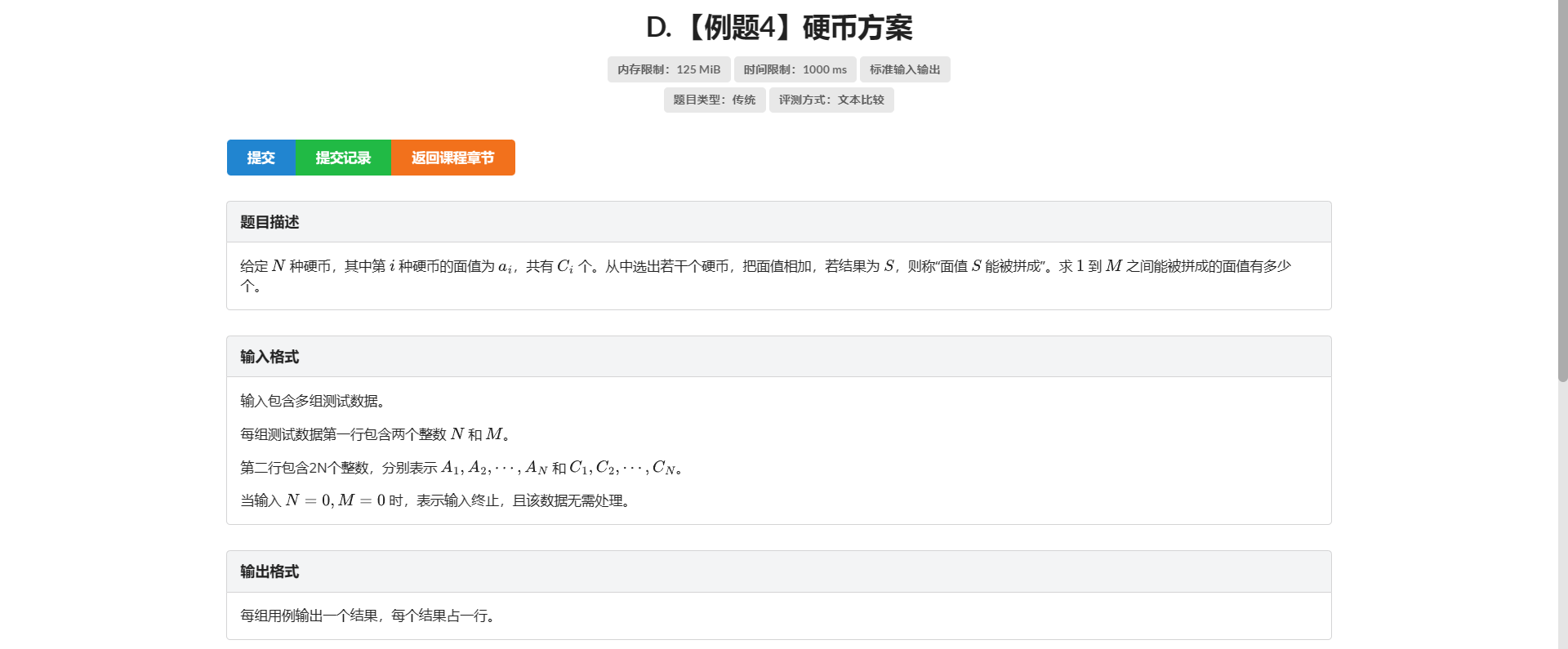
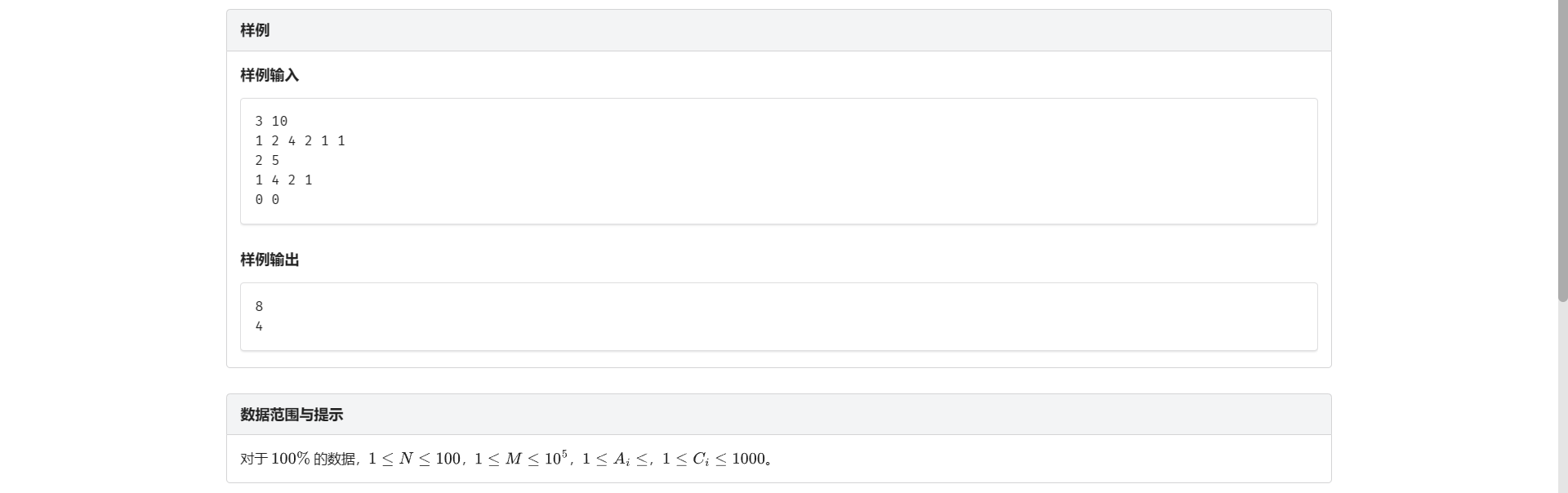
问是否能被拼成 想到暴力转移
但是不太够用 考虑优化
发现瓶颈还是在于数量的枚举
我们换个思路 考虑判断能表示出来的状态和当前状态的数量差是否小于 \(C\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 123;
const int M = 1e5 + 0721;
int sum[N], v[N];
bool f[M];
int cnt[M];
int n, m;
int main() {
while (scanf("%d%d", &n, &m)) {
if (n == 0 && m == 0) break;
int ans = 0;
memset(f, 0, sizeof f );
for (int i = 1; i <= n; ++i) scanf("%d", &v[i]);
for (int i = 1; i <= n; ++i) scanf("%d", &sum[i]);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
memset(cnt, 0, sizeof cnt );
for (int j = 1; j <= m; ++j) {
if (f[j - v[i]] && !f[j] && cnt[j - v[i]] < sum[i]) {
f[j] = 1;
cnt[j] = cnt[j - v[i]] + 1;
}
}
}
for (int i = 1; i <= m; ++i) {
if (f[i])
++ans;
}
printf("%d\n",ans);
}
return 0;
}
E.金明的预算方案
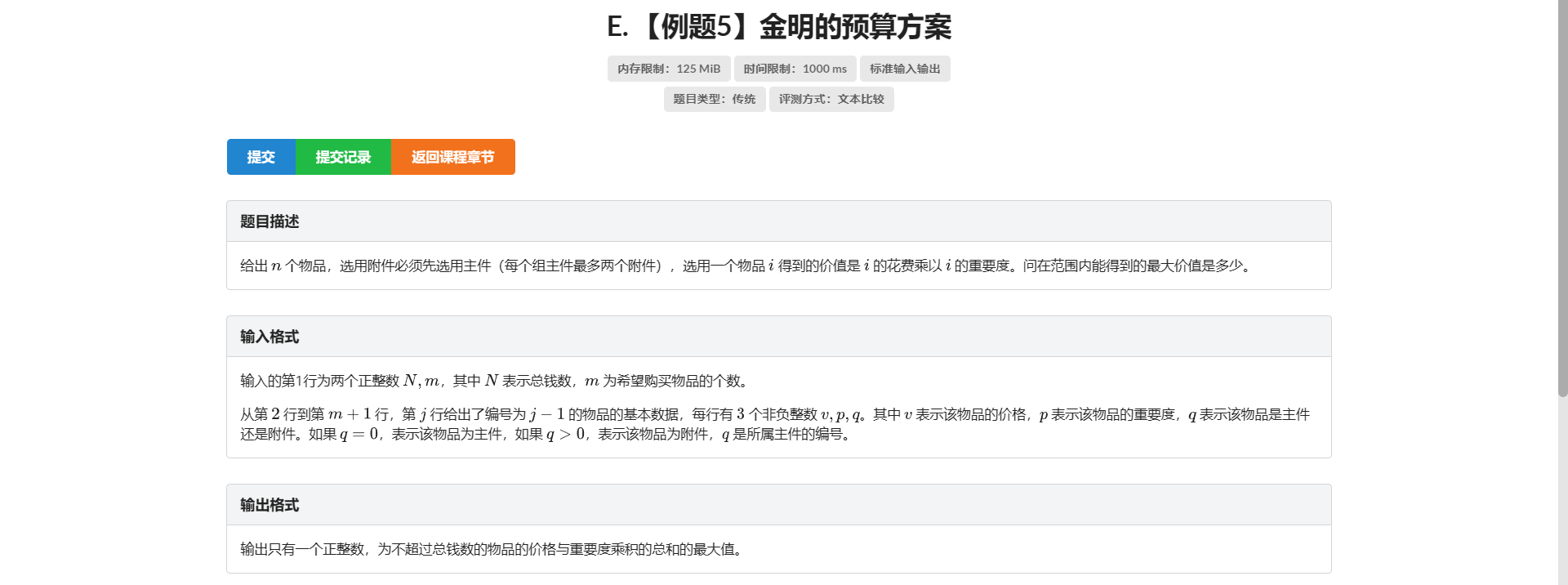
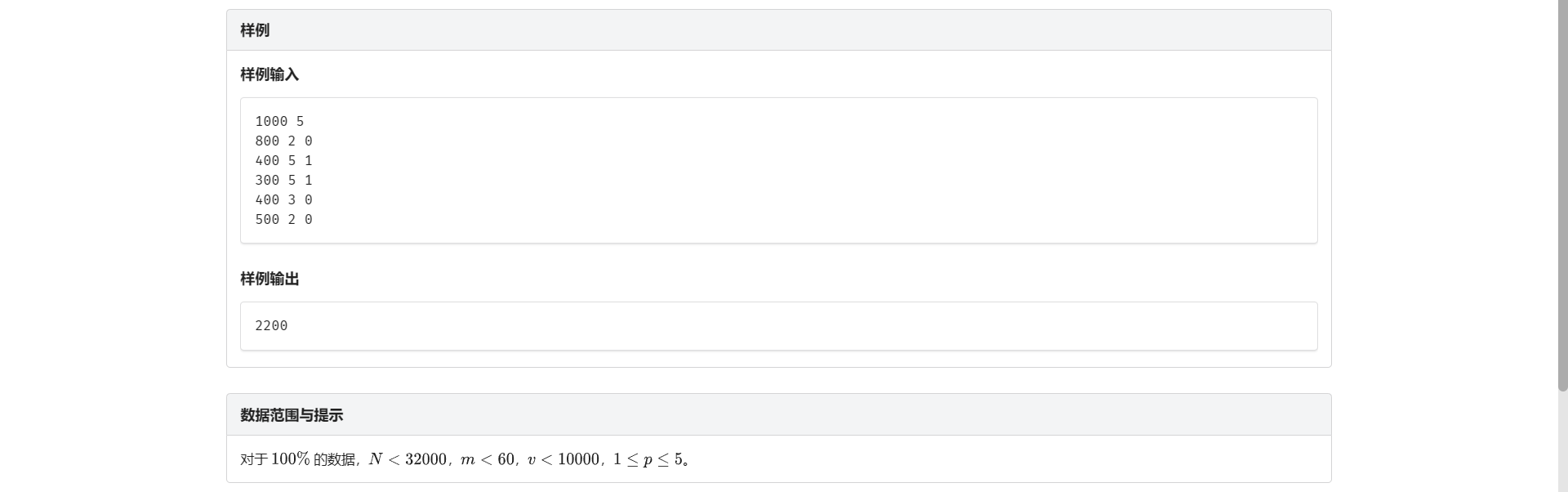
因为一个主件只有两个附件 只有以下几种情况:
- 啥都不选
- 只选一个主件
- 选主件和附件1
- 选主件和附件2
- 主件和两个附件都选上
暴力枚举即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int v[N][3], w[N][3];
int id[N], now[N];
int f[N];
int m, n, cnt;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (z == 0) {
id[i] = ++cnt;
++now[cnt];
w[cnt][0] = x;
v[cnt][0] = x * y;
}
else {
w[id[z]][now[id[z]]] = x;
v[id[z]][now[id[z]]] = x * y;
++now[id[z]];
}
}
for (int i = 1; i <= cnt; ++i) {
if (now[i] == 1) {
for (int j = n; j >= 0; --j) {
if (j >= w[i][0])
f[j] = max(f[j], f[j - w[i][0]] + v[i][0]);
}
} else if (now[i] == 2) {
for (int j = n; j >= 0; --j) {
if (j >= w[i][0])
f[j] = max(f[j], f[j - w[i][0]] + v[i][0]);
if (j >= w[i][0] + w[i][1])
f[j] = max(f[j], f[j - w[i][0] - w[i][1]] + v[i][1] + v[i][0]);
}
}
else {
for (int j = n; j >= 0; --j) {
if (j >= w[i][0])
f[j] = max(f[j], f[j - w[i][0]] + v[i][0]);
if (j >= w[i][0] + w[i][1])
f[j] = max(f[j], f[j - w[i][0] - w[i][1]] + v[i][1] + v[i][0]);
if (j >= w[i][0] + w[i][2])
f[j] = max(f[j], f[j - w[i][0] - w[i][2]] + v[i][2] + v[i][0]);
if (j >= w[i][0] + w[i][1] + w[i][2])
f[j] = max(f[j], f[j - w[i][0] - w[i][1] - w[i][2]] + v[i][0] + v[i][1] + v[i][2]);
}
}
}
printf("%d",f[n]);
return 0;
}
F.求好感度
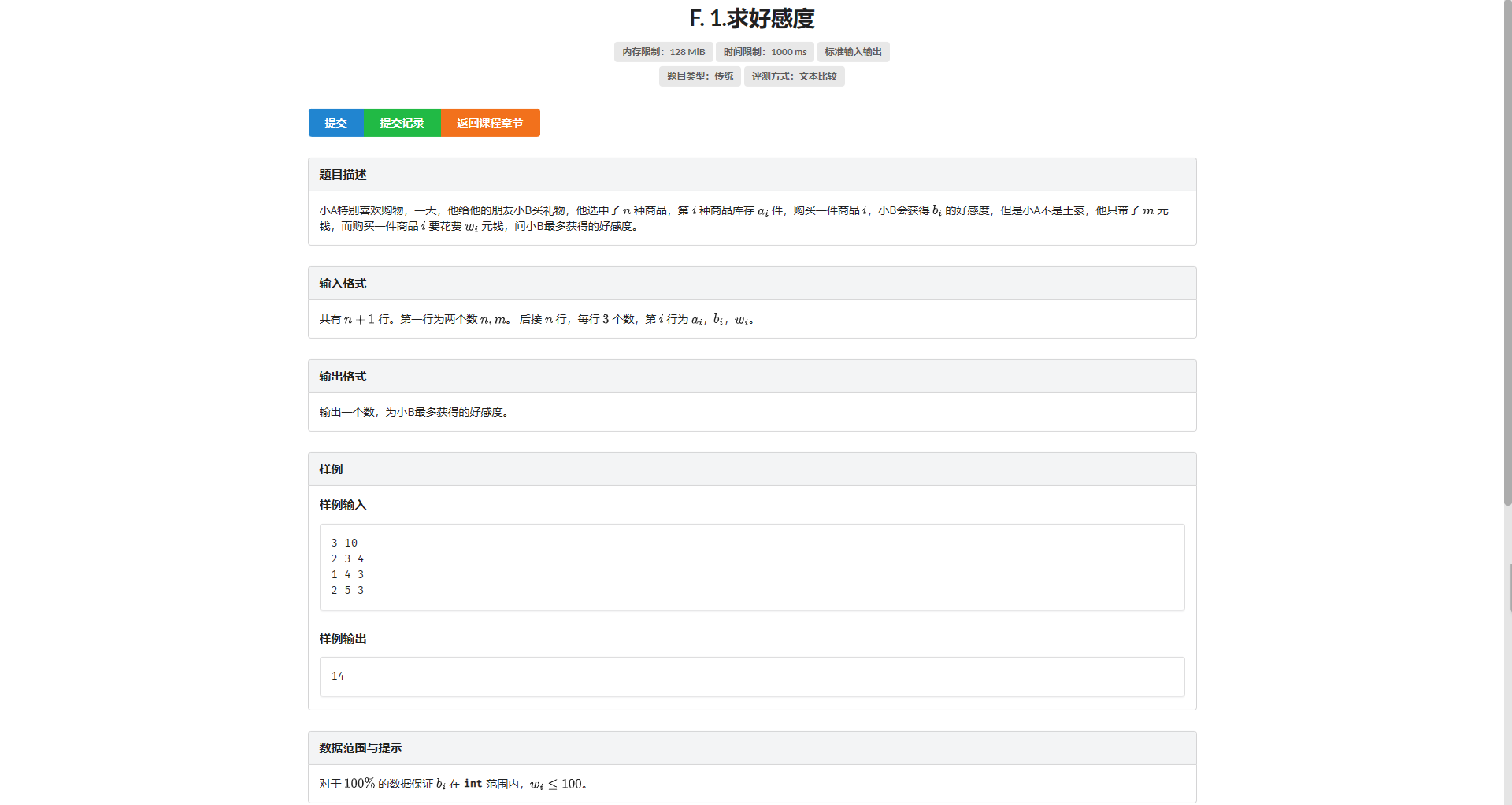
裸多重背包
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
ll f[N], g[N];
int q[N];
int n, m;
void main() {
scanf("%d%d", &n, &m);
while (n--) {
memcpy(g, f, sizeof f);
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
for (int j = 0; j < w; ++j) {
int h = 0, t = -1;
for (int k = j; k <= m; k += w) {
while (h <= t && (k - q[h]) / w > a) ++h;
if (h <= t) f[k] = max(g[k], g[q[h]] + 1ll * (k - q[h]) / w * b);
while (h <= t && g[k] >= g[q[t]] + 1ll * (k - q[t]) / w * b) --t;
q[++t] = k;
}
}
}
printf("%lld\n", f[m]);
}
}
int main() {
steven24::main();
return 0;
}
/*
3 10
2 3 4
1 4 3
2 5 3
*/
G.购买商品
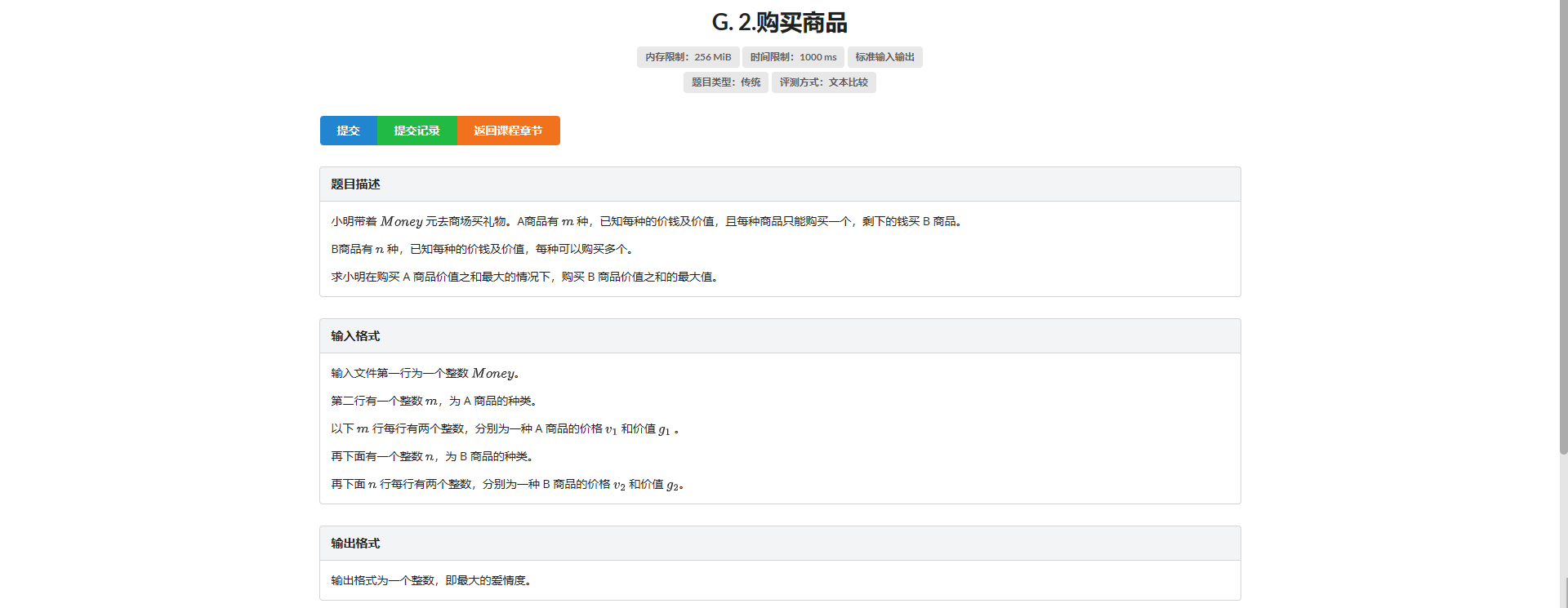
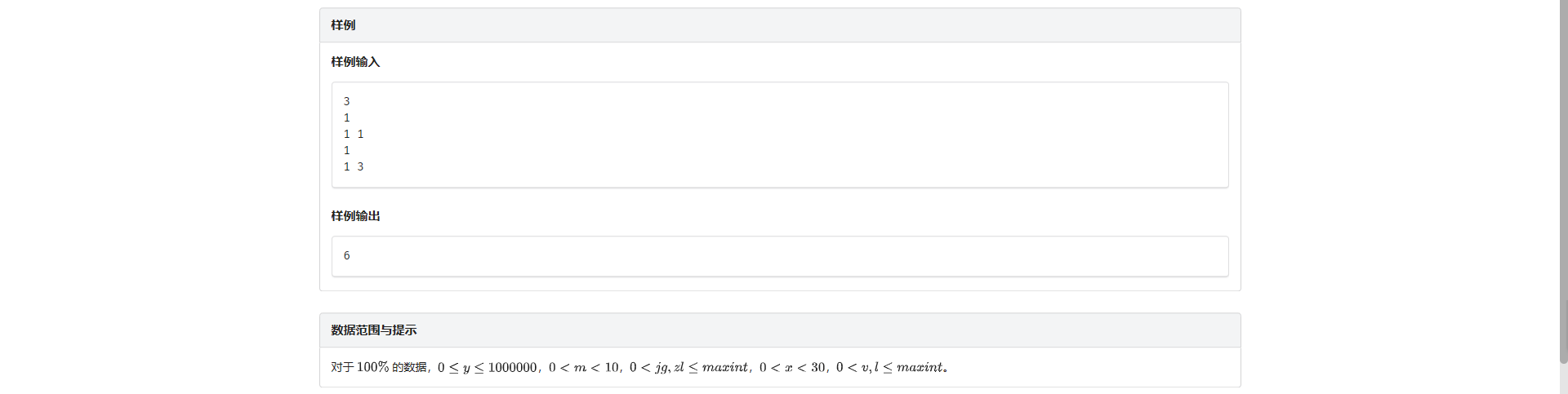
这啥破题面啊。。。
输出:购买 B 商品价值之和的最大值
数据范围:\(Money \le 2 \times 10^5, m \le 20, n \le 3000\) 不需要开 long long
01 背包扫一遍
完全背包扫一遍
做完了
点击查看代码
#include <bits/stdc++.h>
#define ll int
using namespace std;
namespace steven24 {
const int N = 1e6 + 0721;
ll f[N], g[N];
int m, A, B;
struct node {
int v, w;
} a[N], b[N];
void main() {
scanf("%d", &m);
scanf("%d", &A);
for (int i = 1; i <= A; ++i) scanf("%d%d", &a[i].w, &a[i].v);
scanf("%d", &B);
for (int i = 1; i <= B; ++i) scanf("%d%d", &b[i].w, &b[i].v);
for (int i = 1; i <= A; ++i) {
for (int j = m; j >= a[i].w; --j) f[j] = max(f[j], f[j - a[i].w] + a[i].v);
}
ll ans = f[m];
for (int i = 0; i <= m; ++i) {
if (f[i] == ans) {
m -= i;
break;
}
}
for (int i = 1; i <= B; ++i) {
for (int j = b[i].w; j <= m; ++j) g[j] = max(g[j], g[j - b[i].w] + b[i].v);
}
printf("%d\n", g[m]);
}
}
int main() {
steven24::main();
return 0;
}
/*
3
1
1 1
1
1 3
*/
H.魔法开锁
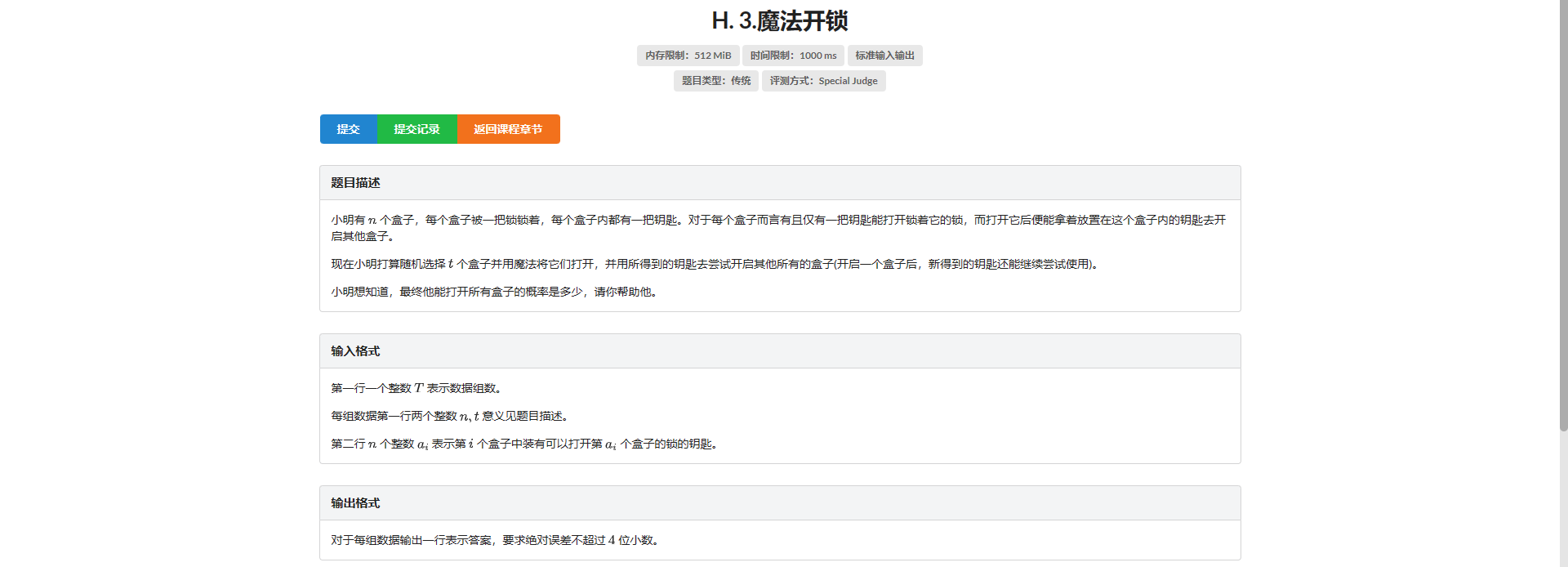
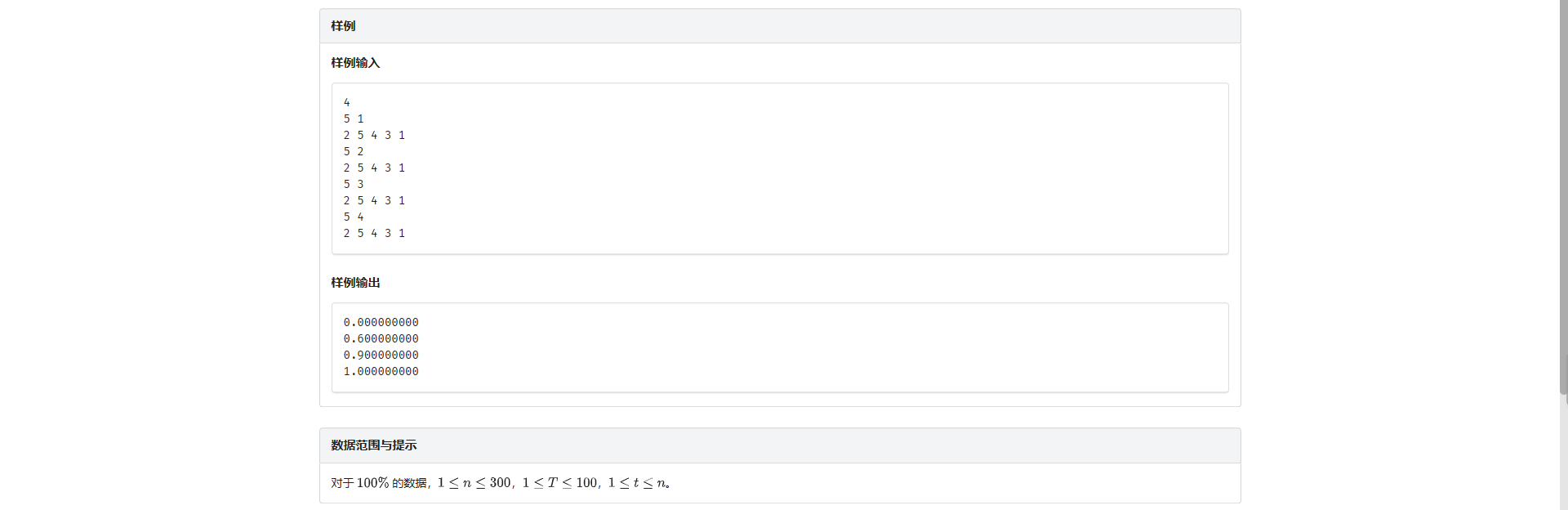
垒球。
想到连边 然后不会了
没想到连边之后每个点出度入度都为 1 所以图一定是若干个不相交的简单环
设 \(f_{i, j}\) 表示前 \(i\) 个环选 \(j\) 个点的合法方案数
转移的时候枚举分配给当前环的点数即可
方案总数就是从 \(n\) 个点中选 \(t\) 个点的方案数
组合数和 \(f\) 数组都要开 double 会炸 long long
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 521;
int n, t, T; //NTT(误
double f[N][N];
int fa[N], tot[N];
double c[N][N];
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void init() {
c[0][0] = 1;
for (int i = 1; i <= 300; ++i) {
c[i][0] = 1;
for(int j = 1; j <= i; ++j) {
c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
// if (c[i][j] < 0) cout << i << " " << j <<" " << c[i][j] << "\n";
}
}
}
void main() {
scanf("%d", &T);
init();
while (T--) {
scanf("%d%d", &n, &t);
memset(tot, 0, sizeof tot);
memset(f, 0, sizeof f);
for (int i = 1; i <= n; ++i) fa[i] = i;
for (int i = 1; i <= n; ++i) {
int x;
scanf("%d", &x);
int fx = find(x), fi = find(i);
fa[fi] = fx;
}
for (int i = 1; i <= n; ++i) ++tot[find(i)];
f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
if (!tot[i]) {
for (int j = 0; j <= t; ++j) f[i][j] = f[i - 1][j];
continue;
}
for (int j = 0; j <= t; ++j) {
for (int k = 1; k <= j && k <= tot[i]; ++k) f[i][j] += f[i - 1][j - k] * c[tot[i]][k];
}
}
printf("%lf\n", f[n][t] / c[n][t]);
}
}
}
int main() {
steven24::main();
return 0;
}
/*
4
5 1
2 5 4 3 1
5 2
2 5 4 3 1
5 3
2 5 4 3 1
5 4
2 5 4 3 1
*/
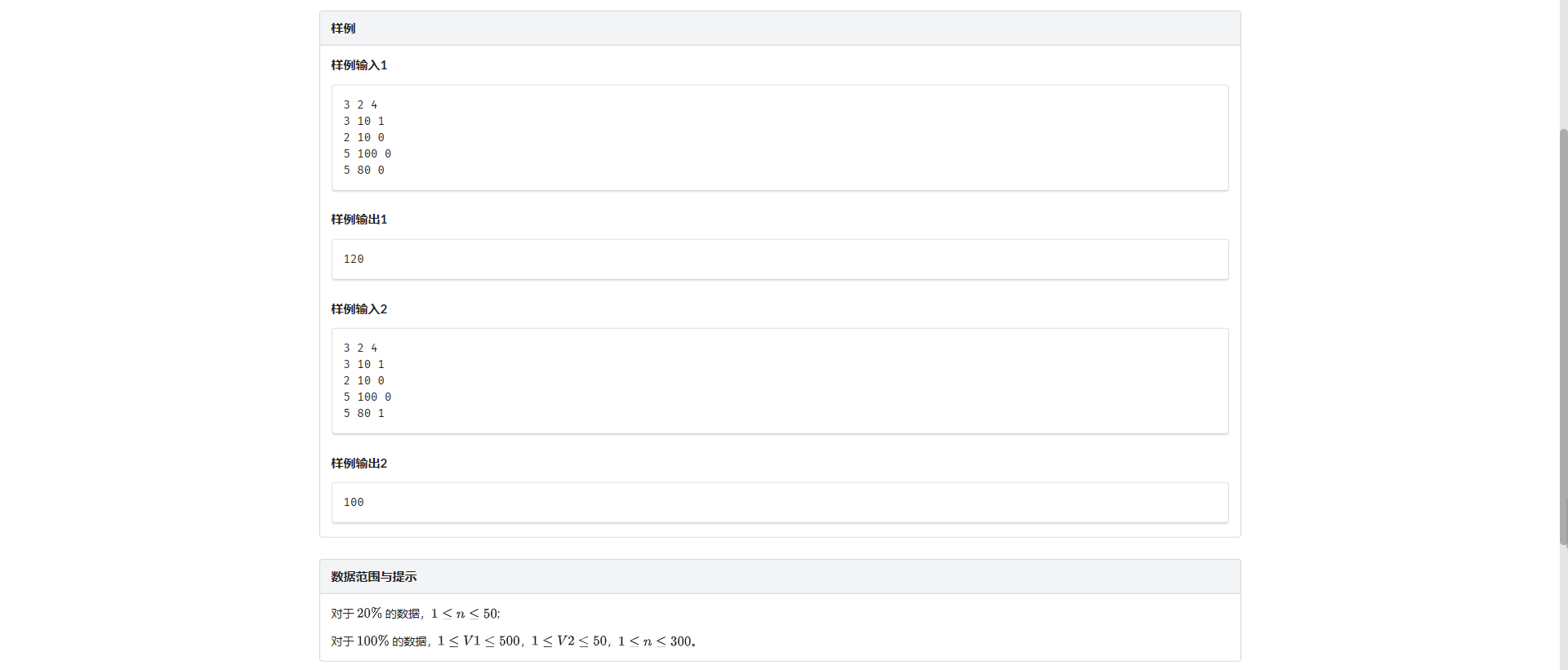
I.购买礼物
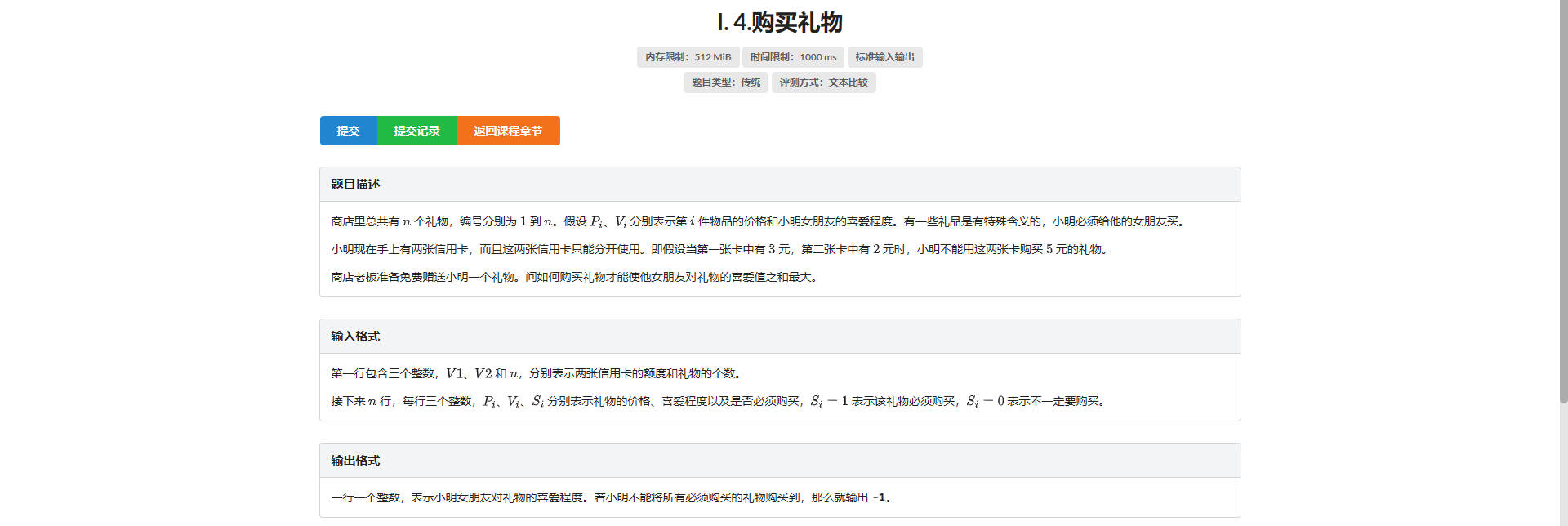
问号。
被自己菜哭了
设 \(f_{i, j, k, pos}\) 表示第 \(i\) 件物品 第一张卡用了 \(j\) 第二张卡用了 \(k\) 用/没用免费机会的花费
转移显然
有几个点需要注意:
- 初值要设成 \(-inf\)
- 判无解看是否 \(>0\)
- 输出答案要把第 \(n\) 层的都扫一遍取 \(\max\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
ll f[301][501][51][2];
int p[301], v[301], s[301];
int n, v1, v2;
void main() {
scanf("%d%d%d", &v1, &v2, &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d%d", &p[i], &v[i], &s[i]);
// cerr << p[i] << " " << v[i] << " " << s[i] << "\n";
}
memset(f, -0x3f, sizeof f);
f[0][0][0][0] = f[0][0][0][1] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= v1; ++j) {
for (int k = 0; k <= v2; ++k) {
if (s[i] == 0) {
f[i][j][k][1] = f[i - 1][j][k][1];
f[i][j][k][0] = f[i - 1][j][k][0];
}
f[i][j][k][1] = max(f[i][j][k][1], f[i - 1][j][k][0] + v[i]);
if (j >= p[i]) {
f[i][j][k][0] = max(f[i][j][k][0], f[i - 1][j - p[i]][k][0] + v[i]);
f[i][j][k][1] = max(f[i][j][k][1], f[i - 1][j - p[i]][k][1] + v[i]);
}
if (k >= p[i]) {
f[i][j][k][0] = max(f[i][j][k][0], f[i - 1][j][k - p[i]][0] + v[i]);
f[i][j][k][1] = max(f[i][j][k][1], f[i - 1][j][k - p[i]][1] + v[i]);
}
}
}
}
ll ans = 0;
for (int i = 0; i <= v1; ++i) {
for (int j = 0; j <= v2; ++j) ans = max(ans, f[n][i][j][1]);
}
if (ans > 0) printf("%lld\n", ans);
else printf("-1\n");
}
}
int main() {
steven24::main();
return 0;
}
/*
3 2 4
3 10 1
2 10 0
5 100 0
5 80 0
*/
J.课题选择
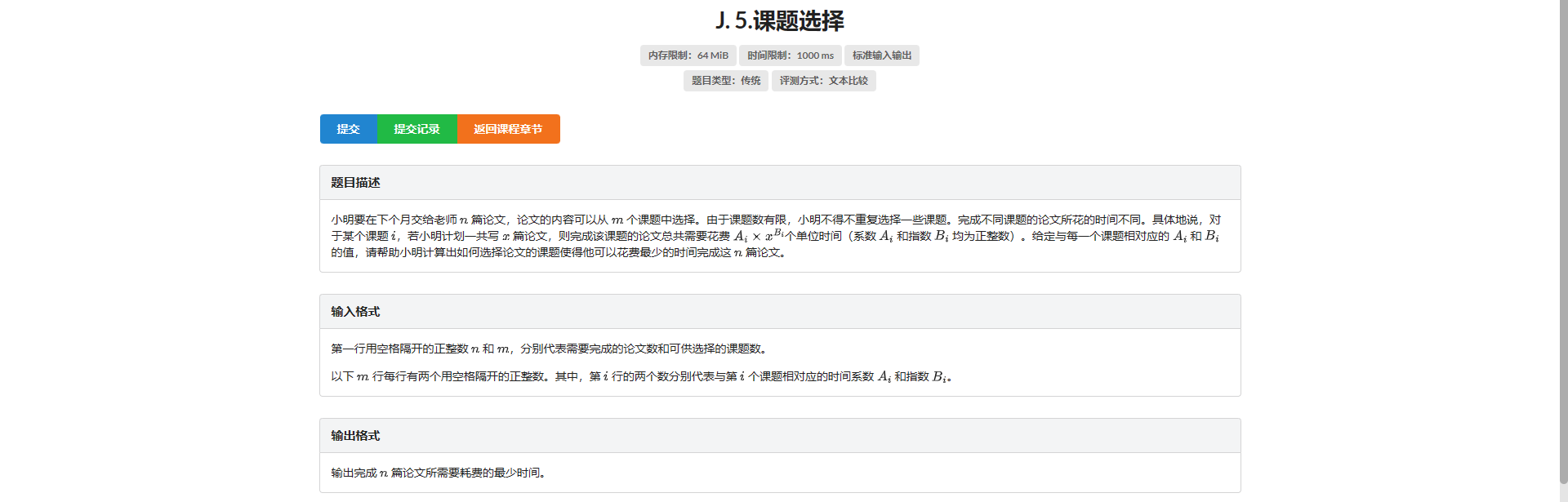
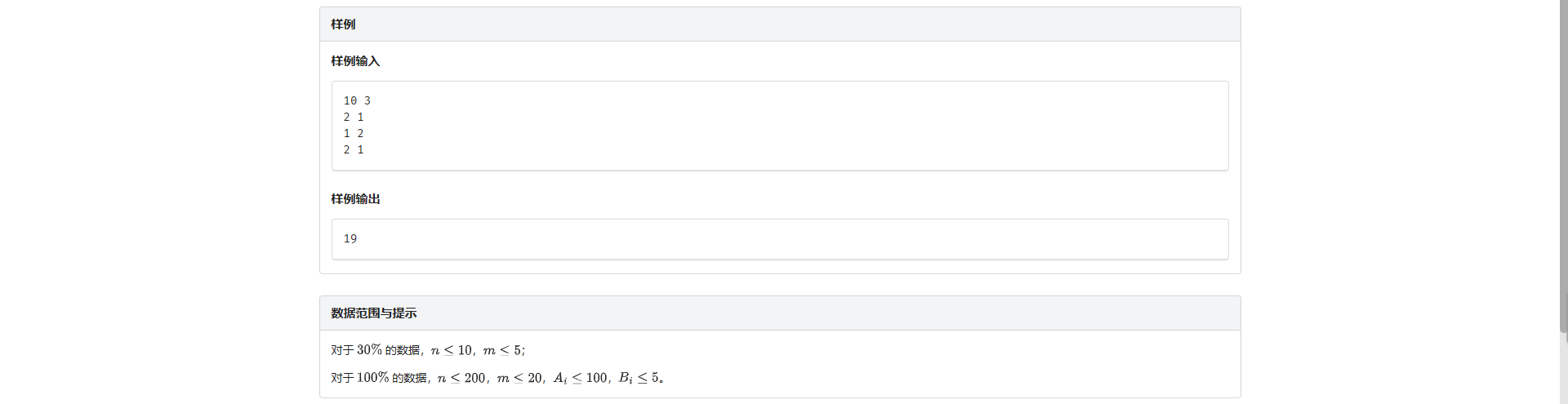
啊?
暴力枚举每个科目写几次即可 复杂度 \(\text{O}(m \times n^2 \times \log B_i)\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
ll f[21][201];
int a[21], b[21];
int n, m;
ll ksm(ll x, int y) {
ll ret = 1;
while (y) {
if (y & 1) ret *= x;
x *= x;
y >>= 1;
}
return ret;
}
void main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) scanf("%d%d", &a[i], &b[i]);
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= m; ++i) {
for (int j = 0; j <= n; ++j) {
for (int k = 0; k <= j; ++k) {
ll cost = 1ll * a[i] * ksm((ll)k, b[i]);
f[i][j] = min(f[i][j], f[i - 1][j - k] + cost);
}
}
}
printf("%lld\n", f[m][n]);
}
}
int main() {
steven24::main();
return 0;
}
/*
10 3
2 1
1 2
2 1
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号