YBTOJ 4.6倍增问题
A.查找编号
一眼二分
但是也可以拿倍增做
我们维护这个点往后 \(2^i\) 格位置的元素大小
然后从大到小枚举 \(2\) 的次数
如果往后 \(2^i\) 格的元素小于要查的 就跳
否则不跳
代码我写的二分就不放了
B.开车旅行


说句题外话 如果你是从 LCA 那章一路刷下来的 你会经历紫题三连发
再吐槽一句 这题题干是真长啊 读着头疼
看起来这两问非常的难 尤其第一问更没什么思路
但是看第二问 显然要做到 \(O(logn)\) 的查询
那么对于第一问 我们如果枚举起点 就是 \(O(nlogn)\) 反正第一问就问一次 完全能过
那么问题就在于如何做到 \(O(logn)\) 查询
进一步发现 实际上如果我选定起点 后续的过程都是固定的
那我就可以倍增预处理出经过 \(2^i\) 步到达的城市
并且因为 \(A\) \(B\) 先开车到达的地方是不一样的 所以要分别处理
注意当 \(i = 0\) 时 开车的人会转换 处理的时候记得特判一下
又因为要判总距离 所以再记录一个 \(dis\) 数组
upd:感觉预处理出前缀和也能做(?
还有一个问题 如何找这个城市之后最高 / 第二高的城市
暴力查找 \(O(n ^ 2)\) 显然是不行的
对此我们可以先排序 然后维护一个双向链表
然后把 \(i\) 从 \(1\) 往 \(n\) 扫 每次移动 \(i\) 就把当前元素从链表中删掉
当然也可以使用 \(multiset\):

点击查看代码
#include <bits/stdc++.h>
#define int long long
#define ll long long
#define db double
using namespace std;
const int N = 1e5 + 0721;
const int inf = 0x7ffffffffffffff;
int f[2][N][21];
ll disa[2][N][21];
ll disb[2][N][21];
int h[N];
int n, m;
struct node {
int id, hi;
friend bool operator<(node a, node b) { return a.hi < b.hi; }
};
multiset<node> s;
void init(void) {
h[0] = inf, h[n + 1] = -inf;
s.insert((node){ 0, inf });
s.insert((node){ 0, inf });
s.insert((node){ n + 1, -inf });
s.insert((node){ n + 1, -inf });
set<node>::iterator p;
for (int i = n; i >= 1; --i) {
int nxta, nxtb;
s.insert((node){ i, h[i] });
p = s.lower_bound((node){ i, h[i] });
// cout<<(*p).id<<endl;
++p;
int h1 = (*p).id;
--p, --p;
int q1 = (*p).id;
++p;
// cout<<h1<<" "<<q1<<endl;
// cout<<abs(h[q1] - h[i])<<" "<<abs(h[h1] - h[i])<<endl;
if (abs(h[q1] - h[i]) <= abs(h[h1] - h[i])) {
// cout<<"nxb= "<<q1<<endl;
nxtb = q1;
--p, --p;
int q2 = (*p).id;
if (abs(h[q2] - h[i]) <= abs(h[h1] - h[i]))
nxta = q2;
else
nxta = h1;
}
else {
// cout<<"nxtb = "<<h1<<endl;
nxtb = h1;
++p, ++p;
int h2 = (*p).id;
if (abs(h[q1] - h[i]) <= abs(h[h2] - h[i]))
nxta = q1;
else
nxta = h2;
}
disa[0][i][0] = abs(h[nxta] - h[i]);
disb[1][i][0] = abs(h[nxtb] - h[i]);
f[0][i][0] = nxta;
f[1][i][0] = nxtb;
// cout<<i<<" "<<disa[0][i][0]<<" "<<disb[1][i][0]<<endl;
// cout<<"i = "<<i<<"时,"<<nxta<<" "<<nxtb<<endl;
}
}
void dp(void) {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) {
if (j == 1) {
f[0][i][1] = f[1][f[0][i][0]][0];
f[1][i][1] = f[0][f[1][i][0]][0];
disa[0][i][1] = disa[0][i][0] + disa[1][f[0][i][0]][0];
disa[1][i][1] = disa[1][i][0] + disa[0][f[1][i][0]][0];
disb[0][i][1] = disb[0][i][0] + disb[1][f[0][i][0]][0];
disb[1][i][1] = disb[1][i][0] + disb[0][f[1][i][0]][0];
}
else {
f[0][i][j] = f[0][f[0][i][j - 1]][j - 1];
f[1][i][j] = f[1][f[1][i][j - 1]][j - 1];
disa[0][i][j] = disa[0][i][j - 1] + disa[0][f[0][i][j - 1]][j - 1];
disa[1][i][j] = disa[1][i][j - 1] + disa[1][f[1][i][j - 1]][j - 1];
disb[0][i][j] = disb[0][i][j - 1] + disb[0][f[0][i][j - 1]][j - 1];
disb[1][i][j] = disb[1][i][j - 1] + disb[1][f[1][i][j - 1]][j - 1];
}
}
}
}
ll la, lb;
void cal(int s, ll x) {
// cout<<"s="<<s<<", x="<<x<<endl;
la = lb = 0;
for (int j = 20; j >= 0; --j) {
// cout<<x<<" "<<j<<" "<<disa[0][x][j]<<" "<<x<<endl;
if (f[0][s][j] && disa[0][s][j] + disb[0][s][j] <= x) {
x -= (disa[0][s][j] + disb[0][s][j]);
la += disa[0][s][j], lb += disb[0][s][j];
s = f[0][s][j];
}
}
}
signed main() {
// freopen("1.txt", "r", stdin);
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) scanf("%lld", &h[i]);
init();
dp();
ll x0;
scanf("%lld", &x0);
db minans, ans;
int ansid;
cal(1, x0);
ansid = 1, minans = db(la) / db(lb);
for (int i = 2; i <= n; ++i) {
cal(i, x0);
ans = db(la) / db(lb);
if (ans < minans) {
minans = ans;
ansid = i;
} else if (ans == minans && h[i] > h[ansid])
ansid = i;
}
printf("%lld\n",ansid);
scanf("%lld", &m);
for (int i = 1; i <= m; ++i) {
int s;
ll x;
scanf("%lld%lld", &s, &x);
cal(s, x);
printf("%lld %lld\n",la,lb);
}
return 0;
C.跑路上班
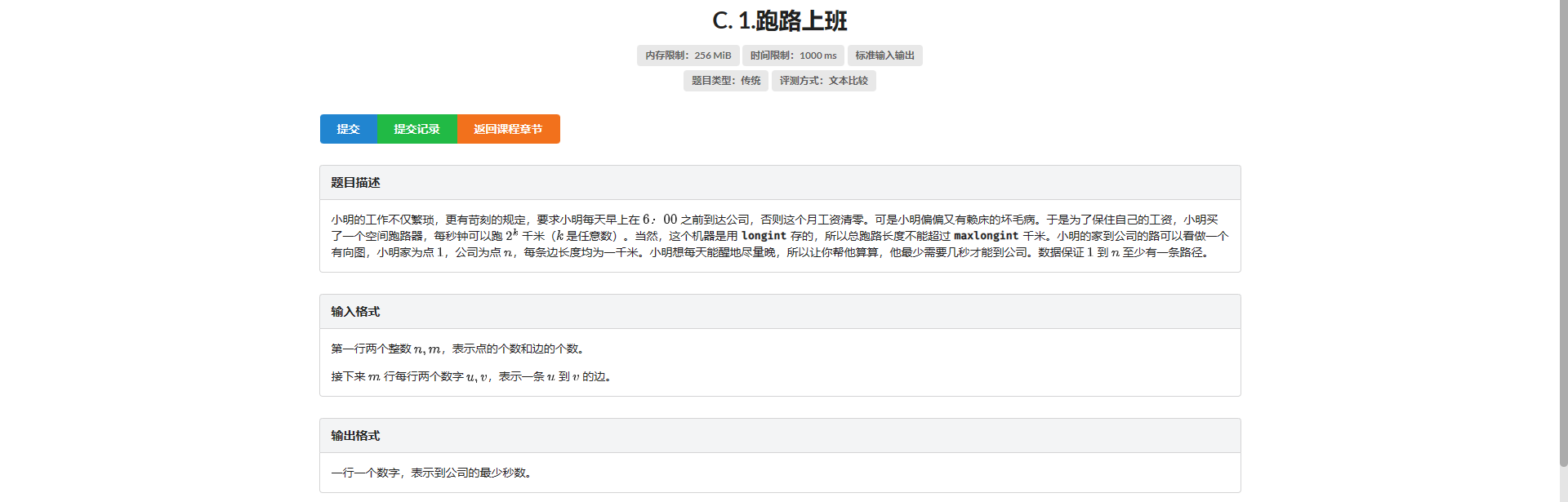
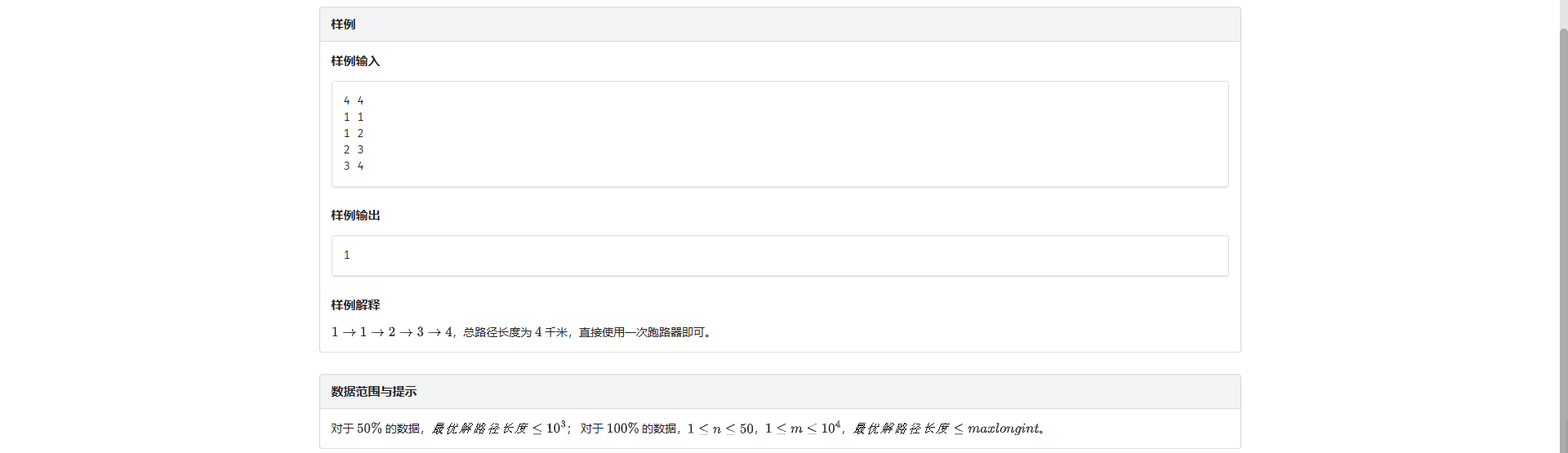
刚开始想的是找一条路使其二进制拆分出来的 1 的数量最少 但是根本不可做
考虑倍增性质
如果我可以用 \(2^k\) 的距离从 \(u \rightarrow v\) \(2^k\) 的距离从 \(v \rightarrow s\) 那么我就可以用 \(2^{k + 1}\) 的距离从 \(u \rightarrow s\)
换言之 我们就可以用 \(1s\) 的时间从 \(u \rightarrow s\)
所以我们用 \(f_{i, j, k}\) 表示从 \(i \rightarrow j\) 是否可以用 \(2^k\) 的距离到达
转移时我们直接像上面那样枚举中间点转移即可
这样我们就可以处理出用 \(1s\) 的时间能到达的点对
然后跑最短路即可 偷懒可以直接跑 floyd
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 52;
const int M = 1e4 + 0721;
int dis[N][N];
bool f[N][N][66];
int n, m;
void main() {
memset(dis, 0x3f, sizeof dis);
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
f[x][y][0] = 1;
dis[x][y] = 1;
}
for (int j = 1; j <= 64; ++j) {
for (int v = 1; v <= n; ++v) {
for (int u = 1; u <= n; ++u) {
for (int s = 1; s <= n; ++s) {
if (f[u][v][j - 1] && f[v][s][j - 1]) {
f[u][s][j] = 1;
dis[u][s] = 1;
}
}
}
}
}
for (int k = 1; k <= n; ++k) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
printf("%d\n", dis[1][n]);
}
}
int main() {
steven24::main();
return 0;
}
/*
4 4
1 1
1 2
2 3
3 4
*/
D.图上查询
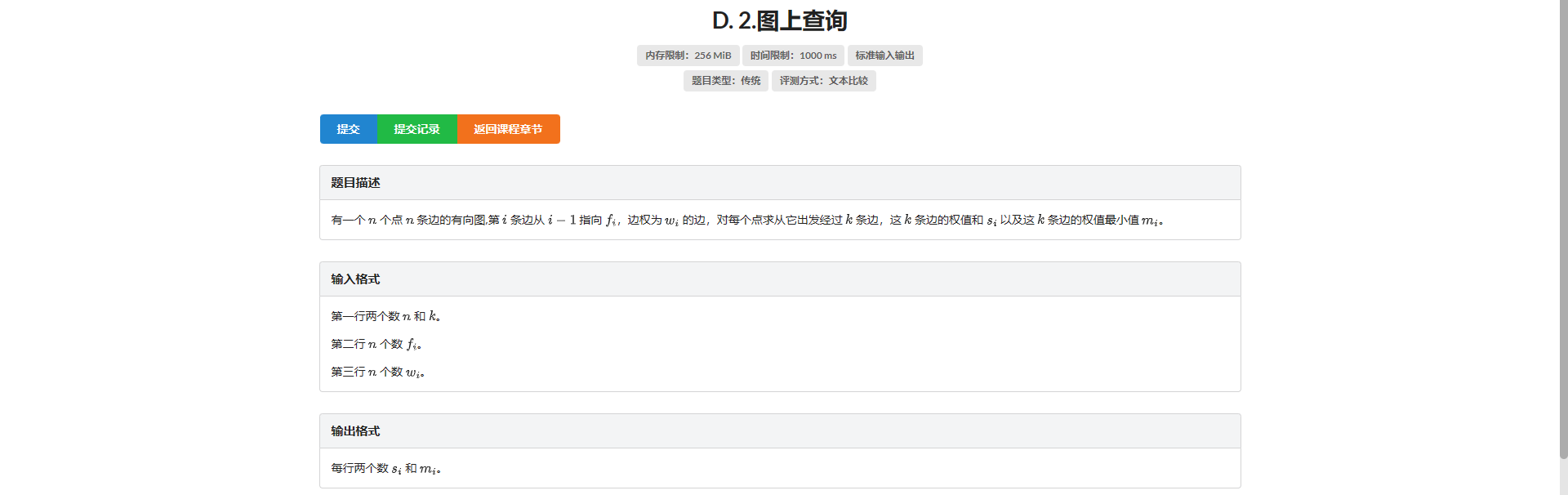
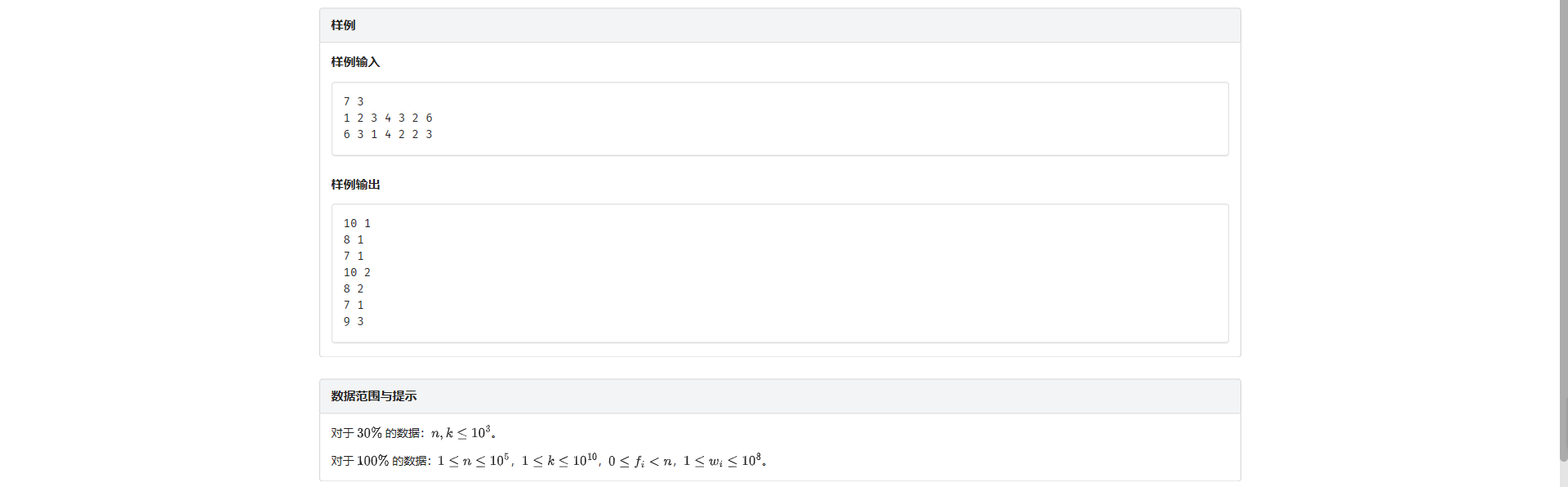
因为 \(k\) 非常大 并且从指定点出发跳指定步的路径是一定的 所以考虑倍增
看出来倍增这题就没啥了( 分别记录从当前点出发跳 \(2^j\) 步的终点/边权和/最小边权
然后统计答案的时候再开个 \(now\) 数组表示这个点当前的位置就行了
有个坑点就是根据题目描述 点的编号是 \(1\) ~ \(n - 1\) 的 读入的时候注意一下即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
ll f[N][36];
int minn[N][36];
int to[N][36];
ll s[N];
int m[N], now[N];
int n;
ll k;
ll calc(int x) {
if (x <= 20) return 1ll * (1 << x);
else return 1ll * (1 << 20) * (1 << (x - 20));
}
void main() {
scanf("%d%lld", &n, &k);
for (int i = 1; i <= n; ++i) {
scanf("%d", &to[i][0]);
++to[i][0];
}
for (int i = 1; i <= n; ++i) {
scanf("%d", &minn[i][0]);
f[i][0] = minn[i][0];
}
for (int j = 1; j <= 35; ++j) {
for (int i = 1; i <= n; ++i) {
to[i][j] = to[to[i][j - 1]][j - 1];
// cout << i << " " << j << " " << to[i][j] << "\n";
minn[i][j] = min(minn[i][j - 1], minn[to[i][j - 1]][j - 1]);
f[i][j] = f[i][j - 1] + f[to[i][j - 1]][j - 1];
}
}
memset(m, 0x3f, sizeof m);
for (int i = 1; i <= n; ++i) now[i] = i;
for (int j = 35; j >= 0; --j) {
if (k & calc(j)) {
for (int i = 1; i <= n; ++i) {
s[i] += f[now[i]][j];
m[i] = min(m[i], minn[now[i]][j]);
now[i] = to[now[i]][j];
}
}
}
for (int i = 1; i <= n; ++i) printf("%lld %d\n", s[i], m[i]);
}
}
int main() {
steven24::main();
return 0;
}
/*
7 3
1 2 3 4 3 2 6
6 3 1 4 2 2 3
*/
E.小明聚会
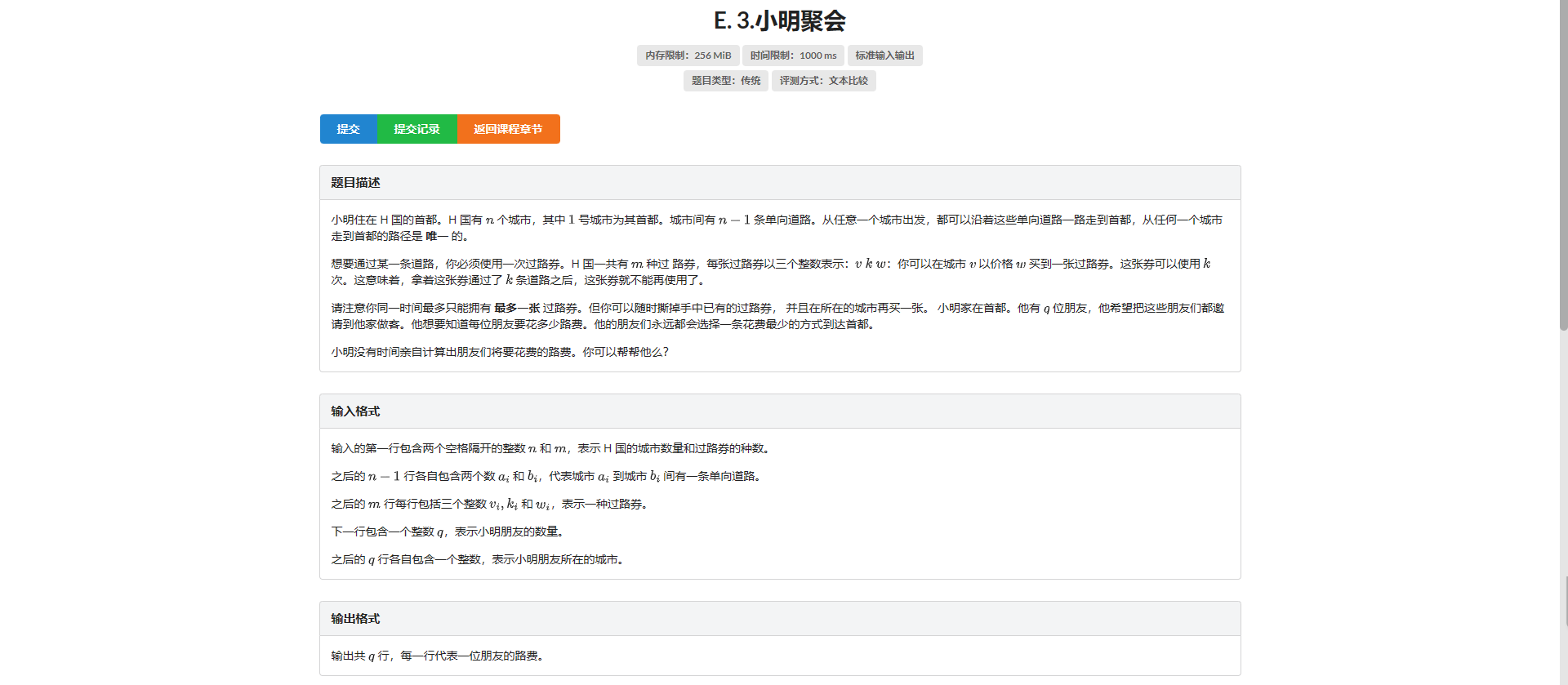
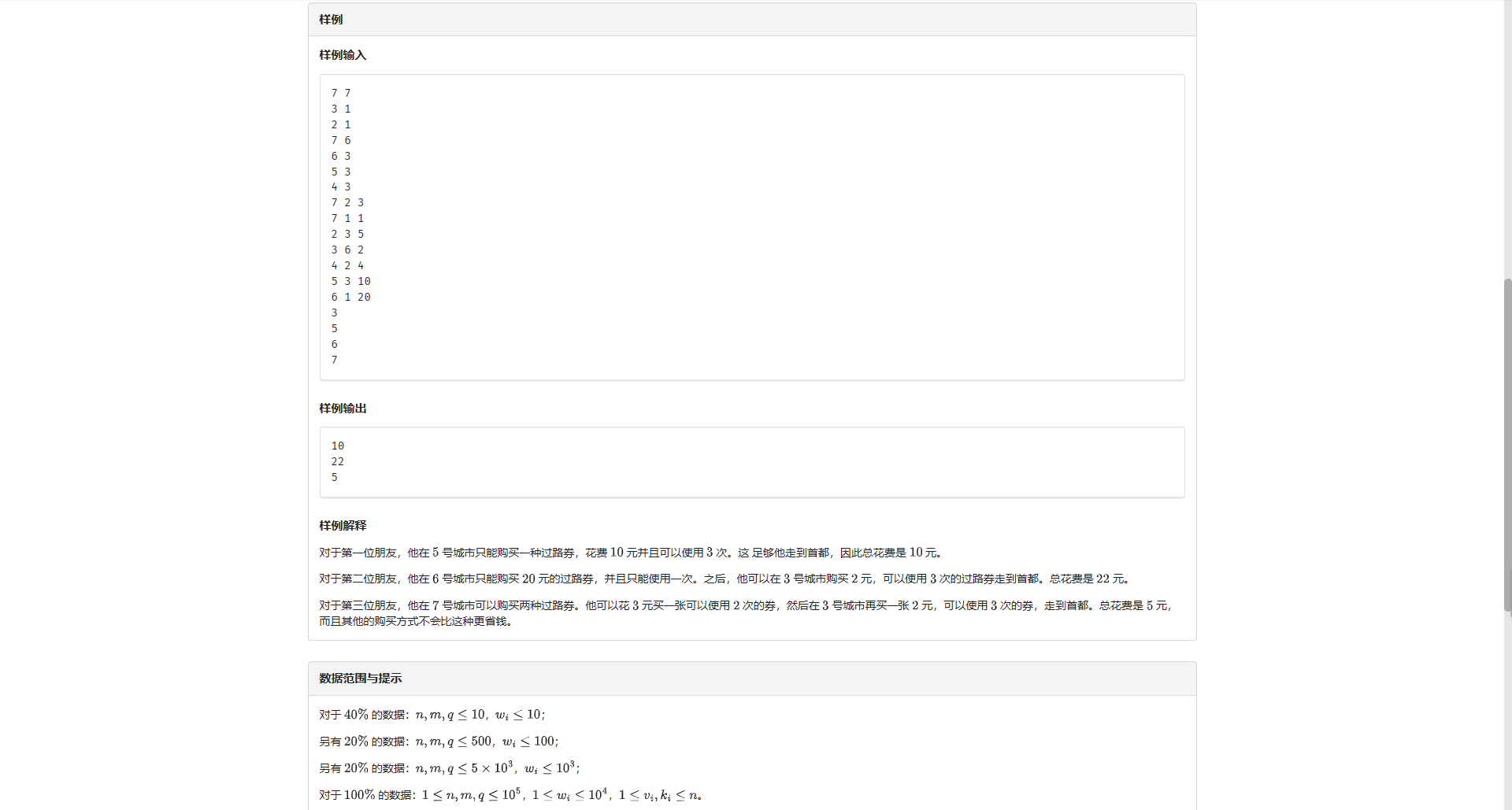
首先很容易想到一个 DP:
设 \(f_i\) 表示从第 \(i\) 个点出发到根节点的最小花费
\(f_i = \min(f_j + cost_x)\)
其中 \(cost_x\) 是可以在 \(i\) 购买的一种购物券 且设该购物券的使用次数为 \(k\) \(j\) 要在 \(i\) 的 \(k\) 级祖先以内
那么转移的时候我们枚举 \(k\) 个祖先即可 暴力转移是 \(\text{O} (nm)\) 的(但是据说可过?)
我们发现这个 \(k\) 级祖先是可以倍增跳的
所以我们设 \(minn_{j, i}\) 表示 \(i\) 的 \(2^j\) 级祖先里 \(f\) 的最小值
那么当我们 dfs 到点 \(i\) 就先把这个点对应的 \(minn\) 数组转移出来(因为它所有的祖先的 \(minn\) 已经转移完了)
然后进行上述转移就可以压到 \(\text{O}(m \log n)\) 了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
const int inf = 0x7fffffff;
int fa[21][N], minn[21][N];
int f[N];
int head[N], nxt[N], to[N], cnt;
int n, m, q;
struct node {
int w, k;
};
vector<node> a[N];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void init() {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) fa[j][i] = fa[j - 1][fa[j - 1][i]];
}
}
void dfs(int x) {
minn[0][x] = f[fa[0][x]];
for (int j = 1; j <= 20; ++j) minn[j][x] = min(minn[j - 1][x], minn[j - 1][fa[j - 1][x]]);
for (auto nod : a[x]) {
int k = nod.k, w = nod.w;
int tmp = inf;
int xx = x;
for (int j = 20; j >= 0; --j) {
if (k >= (1 << j)) {
k -= (1 << j);
tmp = min(tmp, minn[j][xx]);
xx = fa[j][xx];
}
}
f[x] = min(f[x], tmp + w);
// cout << "x: " << x << " " << f[x] << "\n";
}
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
dfs(y);
}
}
void main() {
n = read(), m = read();
for (int i = 1; i < n; ++i) {
int x, y;
x = read(), y = read();
fa[0][x] = y;
add_edge(y, x);
}
init();
for (int i = 1; i <= m; ++i) {
int v, k, w;
v = read(), k = read(), w = read();
a[v].push_back((node){w, k});
}
memset(f, 0x3f, sizeof f);
f[1] = 0;
dfs(1);
q = read();
while (q--) {
int x;
x = read();
printf("%d\n", f[x]);
}
}
}
int main() {
steven24::main();
return 0;
}
/*
7 7
3 1
2 1
7 6
6 3
5 3
4 3
7 2 3
7 1 1
2 3 5
3 6 2
4 2 4
5 3 10
6 1 20
3
5
6
7
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号